-
1、(1)、.(2)、
-
2、如图，△ABC中，AB=AC，点D为CA延长线上一点，DH⊥BC于点H，点F为AB延长线上一点，连接DF交CB的延长线于点E，点E是DF的中点，若BH=2，BE=2BH，则BC=.
-
3、乐乐设计了一个有趣的运算程序：任意写出一个三位数（三位数字相同的除外），重新排列各位数字，使其组成一个最大的数和一个最小的数，然后用最大的数减去最小的数，得到差.重复这个过程··…以579开始，按照此程序运算6次后得到的数是.
-
4、如图，长方形ABCD中，点E为AD上一点，连接CE，将长方形ABCD沿着直线CE折叠，点D恰好落在AB的中点F上，点G为CF的中点，点P为线段CE上的动点，连接PF、PG，若AE=a、ED=b、AF=c，则PF+PG的最小值是（ ）
A、a+b B、b+2c C、a+b+2c D、a+c-b -
5、 等腰三角形的一边长10cm，另一边长4cm，它的第三边长为（ ）A、4cm B、10cm C、6cm D、4cm或 10cm
-
6、一个不透明的袋中装有6个白球，若干个红球，这些球除颜色外完全相同，通过多次摸球试验后发现，摸到白球的频率稳定在0.4附近，则袋中红球的个数是（ ）A、3 B、5 C、9 D、10
-
7、 下列运算正确的是（ ）A、 B、 C、 D、
-
8、一种花瓣的花粉颗粒直径约为0.00000124m，将数据0.00000124用科学记数法表示（ ）A、 B、 C、 D、
-
9、 的值是（ ）A、 B、 C、 D、
-
10、 “图形的变化”是初中几何的重要模块之一，为更好地研究图形在某种变换下具有怎样的性质，某校七年级数学小组设计如下探究活动并提出问题：
如图，在△ABC中，AB=AC，∠BAC=90°，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF，
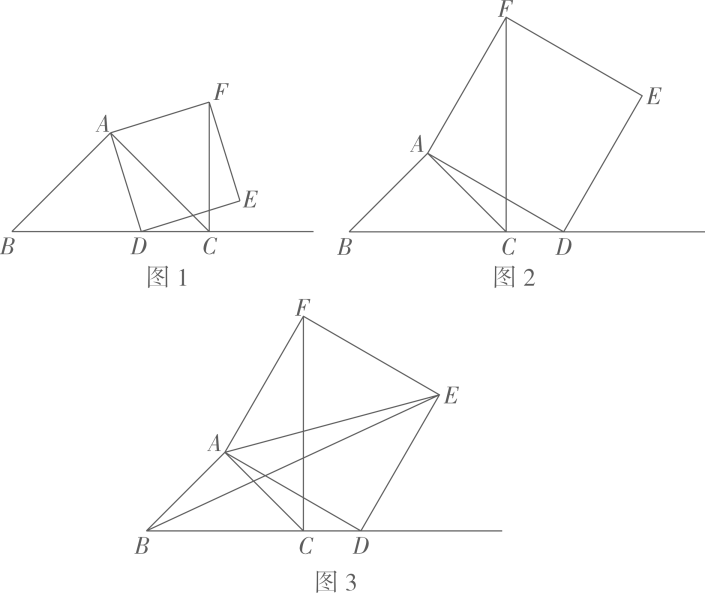(1)、当点D在BC上时，如图1，BD和CF的数量关系为 ， 位置关系为；(2)、当点D运动到BC延长线上时（图2），以上两种关系还成立吗？如果成立，请给出证明。(3)、在（2）的条件下，若AB=AC=1，连接AE，BE，在点D的运动过程中，△ABE的面积是否为定值？若是，请求出该定值，若不是，请说明理由。 -
11、为确保首届“深圳市坪山区环城百公里自行车挑战赛”顺利举行，充分展示坪山魅力，我区串联坪山核心地标，展现“创新坪山、未来之城”的城市形象、自然生态与人文底蕴，制定了详尽的比赛方案。你作为坪山区志愿者团队一员，也参与了活动组织与策划。
此类比赛一般分为精英组和大众组，其中精英组是竞赛类，追求完赛速度；大众组则重视比赛体验，均速相对较慢。比赛沿路设置补给点，严格交通管制并配备收容车，以保证每一辆车安全到达终点。
素材一：
收容车在起点等待比赛开始1小时后发车，以固定速度v（km/h）行驶，在比赛结束时行驶了7个小时，恰好抵达终点（赛程共100km）。选手被收容车追赶上时，收容车会强制接走落后选手。
收容车调度模型：
（1）收容车行驶速度为 ▲ 。收容车行驶时间t（h)与行驶距离s(km)的关系式为 ▲ 。
（2）某选手速度为v=12km/h时，收容车需在距起点多远处接走他？
素材二：组委会监测到精英组第一集团的速度变化如下图：
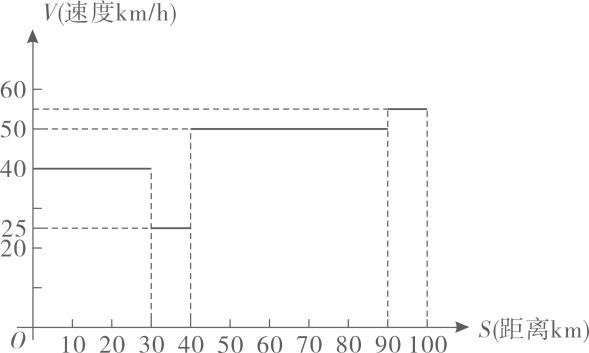
精英组冲奖分析：
（1）估算骑行50km所需时间（提示：分段计算时间并求和）。
（2）若最后10kn保持匀速冲刺，冲刺速度为 ▲ km/h时，选手刚好能和2小时20分的赛会纪录持平。
-
12、如图、在△ABC中，延长AB，在射线AB的延长线上截取DE=AB。
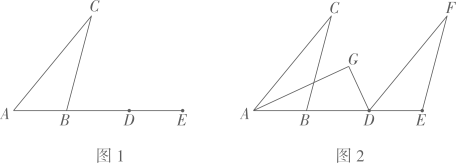
任务1：实践与操作：
①如图1，请用无刻度直尺与圆规作△DEF与△ABC全等（不写作法，保留作图痕迹)
②你作的△DEF与△ABC全等的依据是 ▲ (SSS、SAS、AAS、ASA)
任务2：猜想与证明：如图2，△DEF≌△ABC，AG平分∠CAB，DG平分∠ADF，
试猜想∠G= ▲
②请你求出∠G的度数。
-
13、如图，BE⊥AE，CF⊥AE，垂足分别为E、F，且D是BC的中点，已知DE=3，求DF的长度.
解： ∵BE⊥AE，CF⊥AE
∴∠CFD=∠E=90°
∴D为BC中点
∴ ▲
在△CDF和△BDE中
（ ）
∴△CDF≌△BDE（ ）
∴DF=DE=3（ ）
-
14、如图，正方形网格中，每个小网格的边长是1，△ABC是格点三角形（顶点是网格线交点的三角形），
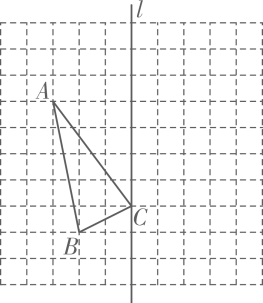(1)、请作出△ABC关于直线l对称的△A1B1C1；(2)、求出△ABC的面积；(3)、试在直线l上找一点P，使PA+PB最小（不写作图过程，保留作图痕迹）， -
15、 x(3y-x)+y(2x-y)+(x-y)2 ， 其中x=3，y=-1.
-
16、计算：(1)、2-2-2025°-（-1)2025(2)、2024×2026-20252
-
17、如图，在四边形ABCD中，AD//BC，点E在BC上且刚好落在AB垂直平分线上，点F是CD中点，EF⊥AF，已知AD=4，BE=7，则CE=.
-
18、如图、将长方形纸片ABCD沿EF折叠，点B、C分别落在点B'、C'处，B'C'与AB相交于点G，如果∠EFC=65°，则∠AGC'=度
-
19、定义一种“四位差运算”的操作：对于一个四位数（四位数字不全相同），将各位数字重新排列组成最大四位数和最小四位数（允许首位为零），用最大数减去最小数得到差。例如，对1234进行一次“四位差运算”，得4321-1234=3087，二次“四位差运算”就是把一次“四位差运算”的结果再做“四位差运算”的操作。则对初始数1234连续进行三次“四位差运算”后的结果是.
-
20、某林业部门统计某种幼树在一定条件下的移植成活率，结果如表所示：
移植总数n
400
1500
3500
7000
9000
14000
成活数m
369
1335
3203
6335
8073
12628
成活的频率
0.923
0.890
0.915
0.905
0.897
0.902
根据表中数据，估计这种幼树移植成活的概率为 (结果精确到0.1).