相关试卷

1、某校为丰富学生的课间活动内容，开设了A：篮球、B：足球、C：跳远、D：跳绳四个活动场地，为了解学生对这4项活动的选择意向，学校随机抽取部分学生进行调查，将数据进行整理并绘制了如下不完整的条形统计图和扇形统计图．
根据以上信息，解答下列问题：

(1)、补全条形统计图；

(2)、扇形统计图中A所对应的圆心角的度数为_____．

(3)、该校共有6000名学生，请你估计该校有多少名学生选择跳绳．

(4)、甲、乙两名学生要选择参加活动，若他们每人从A，B，C，D四类活动中随机选取一类，请用画树状图或列表法，求两人恰好选择同一类活动的概率．

查看解析
2、计算： $- 1^{2025} + \sqrt[3]{27} - {(\frac{1}{2})}^{- 1} + tan 60 °$ ．

查看解析
3、如图，已知 $⊙ P$ 的半径为4，且圆心 $P$ 在边长为4的等边 $△ A B C$ 的三边上运动，点 $B$ 的坐标为 $(1, 1)$ ， $B C ∥ x$ 轴，当 $⊙ P$ 与 $x$ 轴相切时，点 $P$ 的坐标为．

查看解析
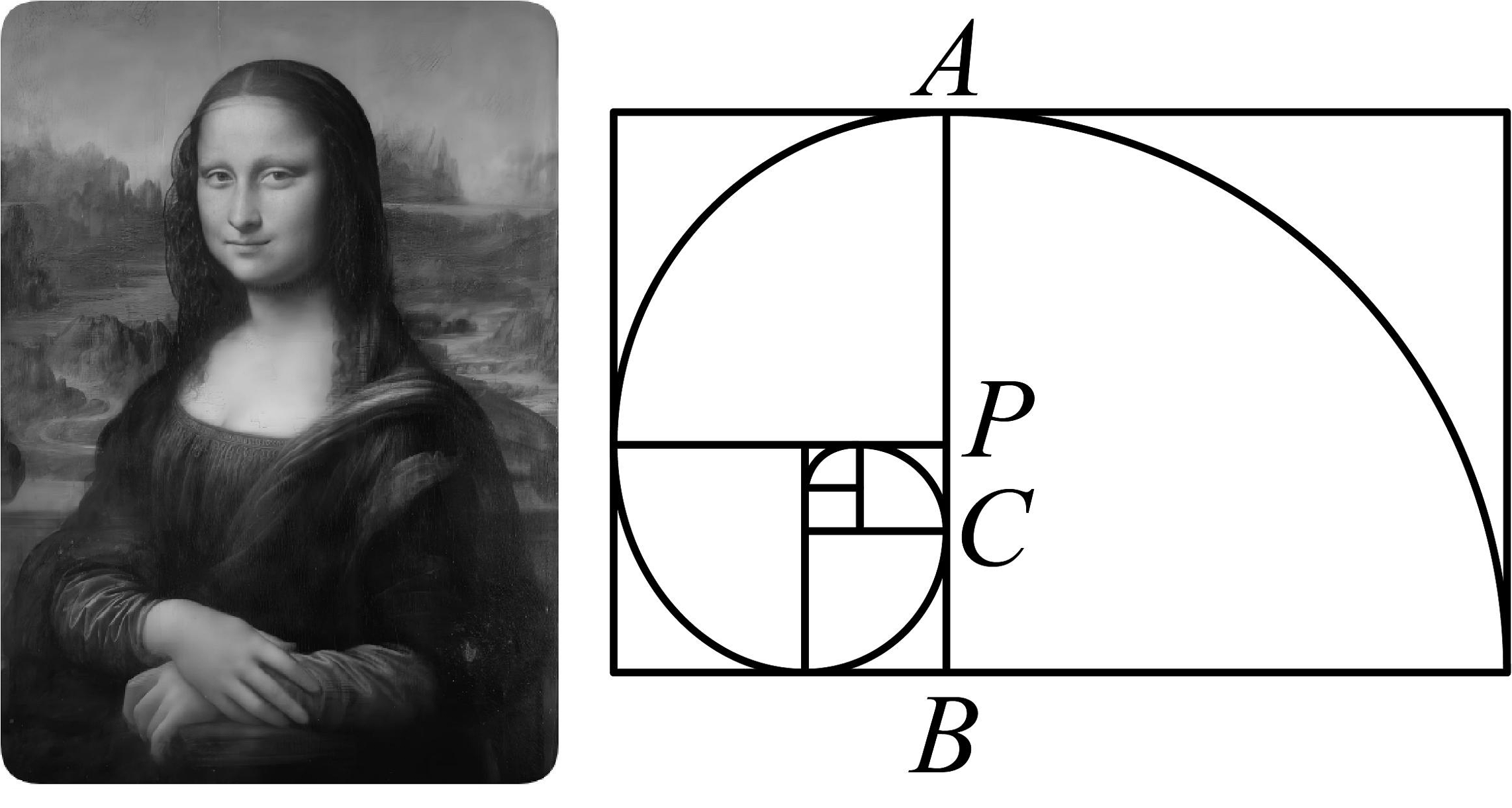
4、鹦鹉螺曲线在人体绘画中不仅是比例工具，更是一种“生长的隐喻”．该曲线的每个半径和前一个半径的比都是黄金比例，即 $\frac{矩半径}{长半径} = \frac{\sqrt{5} - 1}{2}$ ．如图，点 $C$ 是 $B P$ 的黄金分割点 $(B C > P C)$ ，点 $P$ 是 $A B$ 的黄金分割点 $(A P > B P)$ ，若 $B C = 3 - \sqrt{5}$ ，则 $A P =$ ．

查看解析
5、如图，在 $△ A B C$ 中， $A C = B C$ ．以点 $A$ 为圆心，任意长为半径画弧，分别交 $A B, A C$ 于点M，N，再分别以点M，N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，在 $∠ B A C$ 内两弧交于点 $P$ ，射线 $A P$ 交 $B C$ 于点 $D$ ．若 $∠ A D B = 72^{\circ}$ ，则 $∠ C =$ °．

查看解析
6、如图，四边形 $O A B C$ 是平行四边形， $O$ 为坐标原点，点 $C$ 在 $y$ 的正半轴上，点 $A$ 在反比例函数 $y = \frac{m}{x} (x > 0)$ 的图象上，点 $D$ 是线段 $B C$ 与反比例函数图象的交点，若点 $B$ 的坐标为 $(2, 4)$ ，平行四边形 $O A B C$ 的面积为6，则实数 $m$ 的值为．

查看解析
7、甲，乙，丙，丁四名学生进行数学素养能力测试，每人10次测试成绩的平均数 $\bar{x}$ 及方差 $S^{2}$ 如表所示．根据表中数据，要从中选择一名成绩好且发挥稳定的学生参加全国中学生数学能力测评，应选择．
甲
乙
丙
丁
$\bar{x}$
110
98
110
110
$S^{2}$
1.5
0.5
1.1
0.5

查看解析
8、直线y＝x－2与y轴交点坐标是．

查看解析
9、关于 $x$ 的不等式 $2 x - 1 < 3$ 的解集是．

查看解析
10、古典吉他的示意图如图所示， $A_{0}, B$ 分别是上弦枕、下弦枕， $A_{i} (i = 1, 2, \dots, 19)$ 是第 $i$ 品丝．记 $a_{i}$ 为 $A_{i}$ 与 $A_{i - 1}$ 的距离， $L_{i}$ 为 $A_{i}$ 与 $A_{0}$ 的距离，且满足 $a_{i} = \frac{X_{L} - L_{i - 1}}{M}$ ， $i = 1, 2, \dots, 19$ ，其中 $X_{L}$ 为弦长（ $A_{0}$ 与 $B$ 的距离）， $M$ 为大于1的常数，并规定 $L_{0} = 0$ ．若 $X_{L} = 650 mm$ ， $M = 18$ ，则 $\frac{a_{3}}{a_{2}}$ 的值为（）

A、 $\frac{17}{18}$ B、 $\frac{18}{17}$ C、 $\frac{17}{16}$ D、 $\frac{16}{17}$

查看解析
11、如图，以正六边形 $O A B C D E$ 的顶点 $O$ 为圆心， $O A$ 的长为半径画圆，若 $⊙ O$ 的半径为6，则图中阴影部分（弓形）的面积为（）

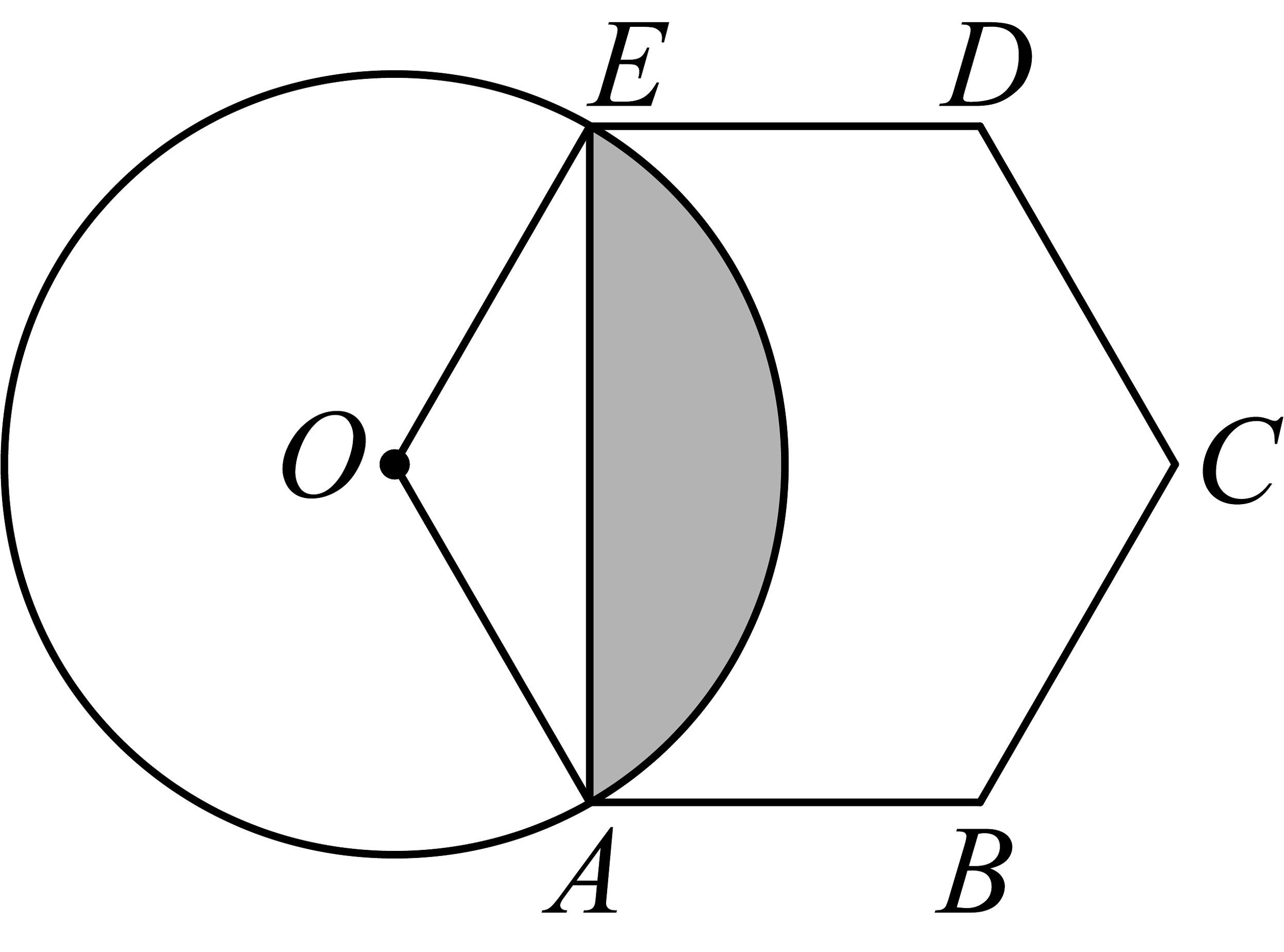A、 $12 π$ B、 $12 π - 18 \sqrt{3}$ C、 $6 π - 9 \sqrt{3}$ D、 $12 π - 9 \sqrt{3}$

查看解析
12、如图，已知在 $▱ A B C D$ 中， $B C = 6$ ，延长 $C D$ 至 $E$ ，使 $D E = \frac{1}{2} C D$ ，连接 $B E$ ，交 $A D$ 于点 $F$ ，则 $D F$ 的长为（）

A、2 B、3 C、4 D、 $2.5$

查看解析
13、以下是9个主要的中国传统节日：春节（农历正月初一）；元宵节（农历正月十五）；端午节（农历五月初五）；七夕节（农历七月初七）；中元节（农历七月十五）；中秋节（农历八月十五）；重阳节（农历九月初九）；腊八节（农历腊月初八）；小年（北方腊月二十三/南方腊月二十四），若从这9个节日中选一个节日，则抽到的节日在农历七月的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{4}{9}$ D、 $\frac{1}{3}$

查看解析
14、计算 $\sqrt{15} \times \sqrt{3}$ 的结果正确的是（）

A、 $\sqrt{5}$ B、 $3 \sqrt{5}$ C、15 D、 $5 \sqrt{3}$

查看解析
15、如图是由正方体组成的几何体，它的俯视图是（）

A、 B、 C、 D、

查看解析
16、下列古文字中，可看作轴对称图形的是（）

A、 B、 C、 D、

查看解析
17、下列四个实数中，绝对值最小的是（）

A、 $- 1$ B、3 C、0.5 D、 $- 5$

查看解析
18、如图，在平面直角坐标系 $x O y$ 中，抛物线 $L$ ： $y = a x^{2} - 2 a x - 3 a (a > 0)$ 与 $x$ 轴交于A，B两点（点 $A$ 在点 $B$ 的左侧），其顶点为 $C$ ， $D$ 是抛物线第四象限上一点．

(1)、求线段 $A B$ 的长；

(2)、当 $a = 1$ 时，若 $△ A C D$ 的面积与 $△ A B D$ 的面积相等，求 $tan ∠ A B D$ 的值；

(3)、延长 $C D$ 交 $x$ 轴于点 $E$ ，当 $A D = D E$ 时，将 $△ A D B$ 沿 $D E$ 方向平移得到 $△ A^{'} E B^{'}$ ．将抛物线 $L$ 平移得到抛物线 $L^{'}$ ，使得点 $A^{'}$ ， $B^{'}$ 都落在抛物线 $L^{'}$ 上．试判断抛物线 $L^{'}$ 与 $L$ 是否交于某个定点．若是，求出该定点坐标；若不是，请说明理由．

查看解析
19、如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ，以 $A B$ 为一边向外作正方形 $A B D E$ ，点 $F$ 为直线 $B C$ 上的一点，连接 $D F$ ，作 $F G ⊥ D F$ 交直线 $A B$ 于点 $G$ ．

(1)、如图 $1$ ，若 $A B = A C$ ，点 $F$ 在线段 $B C$ 上，请直接写出线段 $D F$ 与 $F G$ 的数量关系；

(2)、如图 $2$ ，若 $A B = \sqrt{3} A C$ ，点 $F$ 在线段 $B C$ 上，试探究线段 $B D$ ， $B F$ ， $B G$ 三者之间的数量关系，并证明你的结论；

(3)、若 $A B = \sqrt{3} A C$ ，若 $A B = 6$ ， $D F = 4 \sqrt{2}$ ，请直接写出 $A G$ 的长．

查看解析
20、如图，由边长为1的小正方形构成的网格中，每个小正方形的顶点叫做格点，△ABC的顶点在格点上．
请用无刻度尺按要求作图：

(1)、作△ABC的高AH；

(2)、①找一格点D使AD⊥AC且AD＝AC；
②连接CD，在CD上画出一点F，连AF，使AF将四边形ABCD的面积平分．

查看解析

上一页 1052 1053 1054 1055 1056 下一页跳转

	甲	乙	丙	丁
$\bar{x}$	110	98	110	110
$S^{2}$	1.5	0.5	1.1	0.5