相关试卷
-
1、 某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛.在最近的10次选拔赛中,他们的成绩(单位:cm)折线统计图如图所示:

历届比赛成绩表明,成绩达到5.96m就很可能夺冠.若为了稳妥夺冠,则应选择参赛的运动员是 (填“甲”或“乙”).
-
2、 点(-5,3)到x轴上的距离是 .
-
3、如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC的度数是138°,第二次的拐角∠BCD的度数是 .

-
4、如图,线段AB∥CD,AE∥CF,∠D-∠C=α,EP⊥AB于点P,EM平分∠AEB交AB于点M,则∠PEM的度数是( )
 A、 α B、 α C、α D、2α
A、 α B、 α C、α D、2α -
5、某电梯乘载的质量超过300千克时会响起警示音,已知小华、小欧的体重分别为45千克、70千克.小华进入电梯,警示音没响,小欧在小华之后进入电梯,警示音响起.设电梯在两人进入前已乘载的质量为x千克,则x满足( )A、185<x≤255 B、185≤x<255 C、230<x≤255 D、230≤x<255
-
6、课后延时服务已经落地,为了进一步对课后延时服务进行规范,某校计划在延时服务时间内开展各种社团活动.小明对全校学生进行抽样调查,收集整理拟参加社团活动类型(A.读书交流,B.体育锻炼,C.戏剧说唱,D.手工陶艺)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
 A、样本容量为400 B、类型D所对应的扇形的圆心角为36 C、类型C所占的百分比为30% D、类型B的人数为120人
A、样本容量为400 B、类型D所对应的扇形的圆心角为36 C、类型C所占的百分比为30% D、类型B的人数为120人 -
7、圆圆读一本故事书,第一天读了全书的 , 第二天读了剩下的 , 这时还有36页没读,则她第二天读的页数为( )A、18 B、16 C、36 D、12
-
8、把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
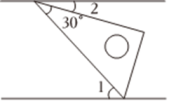 A、26° B、24° C、22° D、20°
A、26° B、24° C、22° D、20° -
9、下列各式中,正确的是( )A、 B、 C、 D、
-
10、下列命题是假命题的是( )A、“对顶角相等”的逆命题是假命题 B、在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c C、两条平行线被第三条直线所截,内错角相等 D、同旁内角互补两直线平行
-
11、关于x的不等式(a-3)x>a-3的解集是x>1,则a的取值范围是( )A、a>3 B、a<3 C、a>1 D、a<1
-
12、已知a,b,c,d是实数,且a-b>c-d,下列说法一定正确的是( )A、若b=d,则a>c B、若a=c,则b>d C、若b<d,则a>c D、若a>c,则b>d
-
13、在平面直角坐标系中,点 , , , 且 , , 满足 .
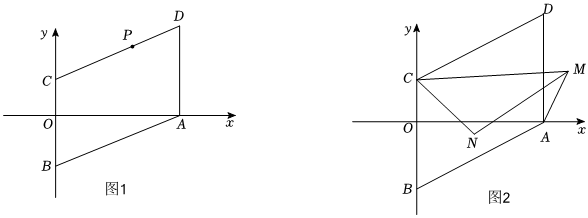 (1)、直接写出 , , ;(2)、如图 , 将线段平移得到线段 , 其中点对应点为 , 点对应点为点,点是线段上一点,求的值;(3)、如图 , 在的条件下,点是线段右侧一点,连接 , , 与的角平分线交于点 , 试探究与之间存在的数量关系.
(1)、直接写出 , , ;(2)、如图 , 将线段平移得到线段 , 其中点对应点为 , 点对应点为点,点是线段上一点,求的值;(3)、如图 , 在的条件下,点是线段右侧一点,连接 , , 与的角平分线交于点 , 试探究与之间存在的数量关系. -
14、综合与实践
【任务驱动】
某校名同学要去参观某科技展览馆,已知该展览馆分为 , , 三个场馆,根据以下素材,解决相应问题【素材收集】
素材:购买张场馆门票和张场馆门票共需元,购买张场馆门票和张场馆门票共需元场馆门票为每张元.
素材:每名同学要选择且只能选择一个场馆参观,且每个场馆都需要有人参观参观当天刚好有优惠活动:每购买张场馆门票就赠送张场馆门票.
【问题解决】
(1)、求场馆和场馆的门票价格.(2)、在出发前,大家的初步参观意向为有名同学想参观场馆,名同学想参观场馆,名同学想参观场馆,在大家的初步参观意向下,按照素材与素材的条件,所需花费的门票总金额为元,求与的值.(3)、到达展览馆后,实际参观三个场馆的人数均有变化,若最终参观场馆的同学人数多于参观场馆的同学人数,按照素材与素材的条件,最终花费的门票总金额为元,请求出符合条件的所有购买方案. -
15、已知方程组的解满足为非正数,为负数.(1)、求的取值范围.(2)、化简: .(3)、在的取值范围内,当为何整数时,不等式的解为 .
-
16、近期,国产大模型强势崛起,在全球科技领域掀起热潮,随着、、豆包、讯飞星火等中国大模型的持续发展和广泛应用,未来中国将在全球领域扮演更加重要的角色市区某校信息科技课外实践小组为了调研该校学生对国产大模型应用场景的了解情况,从全校人中抽取了部分学生展开随机调查,调查结果分为四种:非常了解,比较了解,基本了解,不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
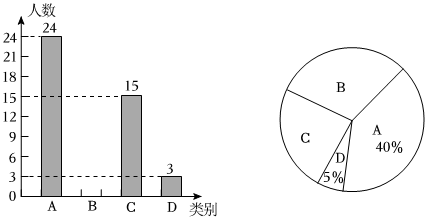
学生对国产大模型应用场景的了解情况
请结合图中所给的信息解答下列问题:
(1)、扇形统计图中所对应的扇形圆心角度数为;(2)、补全条形统计图;(3)、估计全校“比较了解”和“基本了解”国产大模型的应用场景的一共有多少人? -
17、解下列方程或方程组:(1)、;(2)、 .
-
18、如图,直线 , 被直线所截,连接 , , 与相交于点 , , .
 (1)、若 , 求的度数;(2)、点在上,连接 , 若 , 请判定与的数量关系,并说明理由.
(1)、若 , 求的度数;(2)、点在上,连接 , 若 , 请判定与的数量关系,并说明理由. -
19、解不等式,并将解集在数轴上表示出来.
.
-
20、在平面直角坐标系中,点的坐标是若点在第二象限,且点到轴的距离与到轴的距离相等,求的值.