相关试卷

1、下列等式由左边到右边的变形中，属于因式分解的是（　　）

A、（a+1）（a﹣1）＝a²﹣1 B、6x＝2•3x C、x²+2x+1＝x（x+2）+1 D、﹣a²+6a﹣9＝﹣（a﹣3）²

查看解析
2、在数学活动课上，小丽同学将含30°角的直角三角板的一个顶点按如图方式放置在直尺的一边上，测得∠1＝26°，则∠2的度数是（　　）

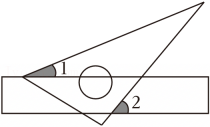A、46° B、64° C、52° D、56°

查看解析
3、若 $\frac{x}{x - 3}$ 有意义，则下列说法正确的是（　　）

A、x＞3 B、x≠3 C、x＞3且x≠0 D、x≠0

查看解析
4、下列运算正确的是（　　）

A、x²•x³＝x⁶ B、（﹣x²）³＝x⁶ C、（x+y）²＝x²+y² D、3x²﹣4x²＝﹣x²

查看解析
5、如图1，在正方形ABCD中，AB＝2，将线段CD绕点C逆时针旋转至CE（∠DCE＜90°），连结DE ， BE ．

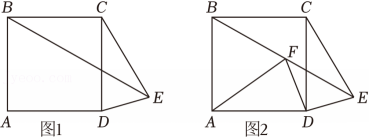(1)、当∠DCE＝30°时，求BE的长度．

(2)、如图2，过点D作DF⊥DE交BE于点F ，连结AF ．
①求证：DF＝DE ．
②当点F是BE中点时，求S_△_DEF与S_△_ABF的面积比．

查看解析
6、已知反比例函数 $y = \frac{2 m}{x}$ 与一次函数y＝m（x﹣1）+2的图象均过点A（x₁ ， y₁），且y₁＞0．

(1)、当x₁＝1时，
①求反比例函数和一次函数表达式．
②若点B（2，n）向左平移3个单位长度，再向上平移2个单位长度后，恰好落在 $y = \frac{2 m}{x}$ 的图象上，求n的值．

(2)、已知点P（2m+3，y₂）在反比例函数 $y = \frac{2 m}{x}$ 的图象上，都有y₂≤2≤y₁ ，求m的取值范围．

查看解析
7、某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，每件衬衫每降价1元，商场平均每天可多售出2件．

(1)、若商场每天要盈利1200元，每件衬衫应降价多少元．

(2)、按这样的降价措施，该商场每天获利能否达到1300元？若能，求出售价；若不能，请说明理由．

查看解析
8、如图，在▱ABCD中，连接AC ．

(1)、用尺规作线段AC的垂直平分线，垂足为点O ，交AD于点E ，交BC于点F ，连结AF ， CE ．（保留作图痕迹，不写作法，标记字母）

(2)、猜想四边形AFCE是什么图形，并加以证明．

查看解析
9、近期在甲、乙两所学校中进行了食堂伙食满意度调查，现从两所学校各随机抽取10名学生的满意度得分数据进行分析（满意度得分用x表示，共分四个等级：A：90≤x≤100，B：80≤x＜90，C：70≤x＜80，D：x＜70）．部分信息如下：
甲学校10名学生满意度得分数据：99，96，92，98，88，88，88，78，74，69；
乙学校10名学生B等级所有满意度得分数据：89，89，88，86，82．
甲、乙学校抽取的学生满意度得分统计表
学校
平均数
中位数
众数
甲
86.3
88
a
乙
86.3
b
89
请根据以上信息解答：

(1)、a＝，b＝．

(2)、求m的值．

(3)、你认为哪所学校的伙食更受学生的欢迎？请说明理由．（写出一条即可）

查看解析
10、如图，四边形ABCD为矩形，对角线交于点O ， DE∥AC交BC延长线于点E ．

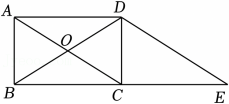(1)、求证：四边形ACED是平行四边形．

(2)、若∠E＝35°，求∠BOC的度数．

查看解析
11、解方程：

(1)、x²+6x﹣7＝0；

(2)、4x（2x+1）＝3（2x+1）．

查看解析
12、计算：

(1)、 $\sqrt{8} + \sqrt{3} \times \sqrt{6}$ ．

(2)、 $\frac{\sqrt{2}}{\sqrt{6} - \sqrt{2}}$ ．

查看解析
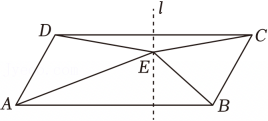
13、如图，在▱ABCD中，AD＝4，AB＝10，∠DAB＝60°，点E为▱ABCD内一点且在CD的垂直平分线l上，连结DE ， CE ， AE ， BE ，当∠EBA＝2∠EAB 时，AE的长为．

查看解析
14、如图，反比例函数 $y = \frac{k}{x} (k ＞ 0)$ 的图象经过▱OABC的顶点C ，并交AB于点D ，已知点D是AB的中点，连结OD ， CD ，若△OCD的面积为3，则k的值为．

查看解析
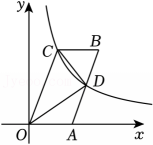
15、如图，△ABC中，D是BC边的中点，AE平分∠BAC ， AE⊥BF于点E ，已知AB＝8，AC＝14，则DE的长为．

查看解析
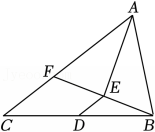
16、在某次歌唱比赛中，小陈“演唱技巧”和“舞台表现”得分分别为9分，8分，若“演唱技巧”和“舞台表现”的权重分别是80%和20%，则小陈的最终得分为分．

查看解析
17、一元二次方程x²﹣5x+a＝0的一个解为x₁＝1，则另外一个解x₂＝．

查看解析
18、如图，等腰△ABC中，AB＝AC＝4，AC＝2BC ，点D ， F是AB边上的动点，且AD＝BF ，过点D ， F作BC的平行线交AC于点E ， G ．下列两条线段的和，不随D ， F的运动而改变的是（　　）

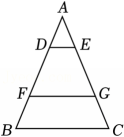A、AD+DF B、DE+FG C、A D、+DE D．DF+FG

查看解析
19、已知A（m﹣2，y₁），B（m ， y₂）两点反比例函数 $y = \frac{- 1}{x}$ 的图象上，则下列判断正确的是（　　）

A、当m＜0时，0＜y₂＜y₁ B、当0＜m＜2时，y₂＜0＜y₁ C、当m＞0时，0＜y₂＜y₁ D、当m＞2时，y₂＜y₁＜0

查看解析
20、随着全球能源危机的逐渐加重，太阳能发电行业发展迅速．全球太阳能光伏应用市场持续稳步增长，2020年全球装机总量约600GW ，预计到2022年全球装机总量达到864GW ．设全球新增装机量的年平均增长率为x ，则可列的方程为（　　）

A、600（1+2x）＝864 B、600+2x＝864 C、（600+x）²＝864 D、600（1+x）²＝864

查看解析

上一页 409 410 411 412 413 下一页跳转

学校	平均数	中位数	众数
甲	86.3	88	a
乙	86.3	b	89