相关试卷
-
1、已知 , 则 .
-
2、 因式分解:
-
3、 使分式在实数范围内有意义,则的取值范围是 .
-
4、 在长方形中, , 有三张边长分别为的正方形纸片 , 蛟蛟将纸片按图①方式放置,发现其中未被纸片覆盖的阴影部分周长为 , 川川将纸片按图②方式放置,发现其中未被纸片覆盖的阴影部分周长为 , 则( )
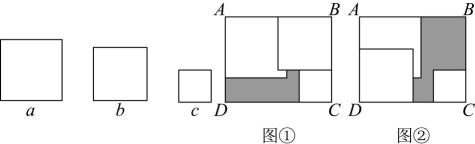 A、2 B、 C、 D、
A、2 B、 C、 D、 -
5、 在中,是边上的中线,若 , 则的取值范围是( )A、 B、 C、 D、
-
6、 “竹下忘言对紫茶,全胜羽客醉流霞.”茶,是承载着文人雅趣的中国传统文化.某茶具厂需生产5400套茶具,原计划由慢车间单独生产,现改进技术,快车间每天生产的茶具数量是慢车间的倍,由快车间单独生产可以提前10天完成,设慢车间每天生产茶具套,下列方程正确的是( )A、 B、 C、 D、
-
7、 若商品的进价为 , 售价为 , 则毛利率 , 把这个公式变形成已知 , 求的公式,应为( )A、 B、 C、 D、
-
8、 如图,在中,、分为、的中点,过点作 , 垂足为 , 若 , , 则( )
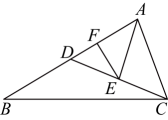 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
9、 如图,点、、、在同一条直线上, , , 需要再补充一个条件,使 . 以下补充条件中,错误的是( )
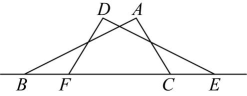 A、 B、 C、 D、
A、 B、 C、 D、 -
10、 某校统计了100名学生的身高数据并分成6组,如下表:
组号
1
2
3
4
5
6
频数
20
19
17
18
14
则第4组数据的频率为( )
A、0.15 B、0.13 C、0.12 D、0.18 -
11、 将的值均扩大为原来的2倍,下列分式的值不变的是( )A、 B、 C、 D、
-
12、 若多项式因式分解后的结果是 , 则的值是( )A、10 B、 C、 D、13
-
13、 计算的值是( )A、 B、 C、 D、1
-
14、 如图1,已知四边形是正方形,点分别是边上的点(不与正方形的顶点重合),且满足 , 连结相交于点 .
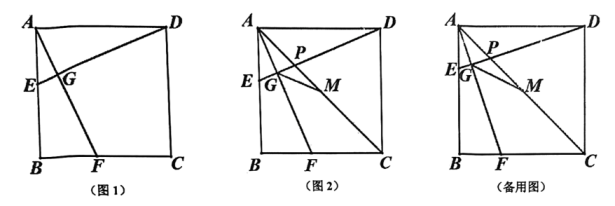 (1)、求证:;(2)、如图2,连结交于点 , 作的角平分线交于点 .
(1)、求证:;(2)、如图2,连结交于点 , 作的角平分线交于点 .①当时,求的值;
②试猜想之间满足的数量关系,并证明.
-
15、 如图1,有一张长为 , 宽为的长方形硬纸片.
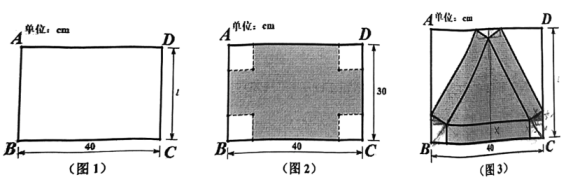 (1)、若裁去角上的四个小正方形之后,折成如图2所示的无盖纸盒,当 , 纸盒的底面积为时,求裁去的正方形边长是多少?(2)、若裁去部分图形后,折成如图3所示底面是正三角形的无盖纸盒,则此时的长为多少?当纸盒的底面积与侧面积(三个长方形的面积)相等时,底面正三角形的边长是多少?
(1)、若裁去角上的四个小正方形之后,折成如图2所示的无盖纸盒,当 , 纸盒的底面积为时,求裁去的正方形边长是多少?(2)、若裁去部分图形后,折成如图3所示底面是正三角形的无盖纸盒,则此时的长为多少?当纸盒的底面积与侧面积(三个长方形的面积)相等时,底面正三角形的边长是多少? -
16、 观察以下式子:记 , 则
①;
②;
(1)、计算观察】; . (直接写出结果即可)(2)、【归纳验证】猜想:(为正整数);并证明.(3)、【应用推广】令 , 计算的值. -
17、 如图,一次函数的图像与反比例函数的图像交于点 , .
 (1)、求的值和一次函数的表达式;(2)、直接写出关于的不等式的解集.
(1)、求的值和一次函数的表达式;(2)、直接写出关于的不等式的解集. -
18、 某班为选拔一名选手参加校知识竞赛,从自愿报名、综合表现等角度确定了甲、乙两名考察对象,在学校组织的辅导过程中,共安排了6次测试,满分10分,每次测试具体得分如图.

得分对象
平均数(分)
中位数(分)
众数(分)
方差(分2)
甲
7
7
7
③
乙
7
①
②
3.2
(1)、将表格补充完整(2)、请结合历次测试成绩,你将推荐谁参加校知识竞赛,并说明理由. -
19、 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF ,
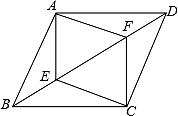 (1)、求证:AE=CF;(2)、求证:四边形AECF的平行四边形.
(1)、求证:AE=CF;(2)、求证:四边形AECF的平行四边形. -
20、 计算:(1)、(2)、 .