相关试卷
-
1、已知: 是 的内接三角形,(1)、如图 , 、 分别为 、 上的高线,交于点 ,若 , ,求 的半径;
 (2)、如图 ,分别作 、 的角平分线,交于点 ,作 ,交 于点 ,连结 ,交 于点 ,若 ,求 的长.
(2)、如图 ,分别作 、 的角平分线,交于点 ,作 ,交 于点 ,连结 ,交 于点 ,若 ,求 的长.
-
2、已知二次函数 .(1)、当 时,函数的最大值与最小值之差为 2,求 的值;(2)、若 恒成立,求 的取值范围.
-
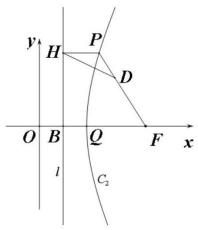
3、将反比例函数 的图像绕着原点 顺时针旋转 得到新的双曲线图像 (如图所示),若直线 轴, 为 轴上的一个定点,已知,图像 上的任意一点 到 的距离与直线 的距离之比为定值,记为 ,即 .
 (1)、若直线 经过点 , 点的坐标为(4,0),且 ,求双曲线 的解析式;(2)、如图,若直线 经过点 ,双曲线 的解析式为 ,且
(1)、若直线 经过点 , 点的坐标为(4,0),且 ,求双曲线 的解析式;(2)、如图,若直线 经过点 ,双曲线 的解析式为 ,且为双曲线 在第一象限内图像上的动点,连接 为线段 上靠近点 的三等分点,连接 ,在点 运动的过程中,当 时,求点 的横坐标.
-
4、对于两个多项式,若 ,满足下列两种情形之一: ; ② ; 则称多项式 为“较大” 多项式,多项式 为“较小” 多项式.对于两个多项式 和 ,若将 和 中 “较大” 多项式和 “较小” 多项式的差记作 ,则称这样的操作为一次 “佳选作差” 操作; 再对 和 进行 “佳选作差” 操作得到 ,以此类推,经过 次操作后得到的序列 称为 “佳选作差” 序列 . 现对 进行 次 “佳选作差” 操作得到 “佳选作差” 序列 ,(1)、 求 ;(2)、求 .
-
5、 如图,已知在 Rt 中, ,点 为 的中点,连结 ,点 为平面内一点, ,连结 ,交 于点 ,且 则 的长为.

-
6、 已知互不相等的实数 满足 ,则 .
-
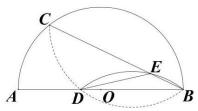
7、如图,点 是半圆 上一点,将弧 沿弦 折叠交直径于点 ,再将弧 沿 翻折交 于点 ,连结 ,若 , 则线段 的长为.
-
8、阅读理解: 对于三个数 ,用 表示三个数中的最小值. 例如: ,则 的最大值为.
-
9、已知 ,满足 ,则使反比例函数 的图像经过二、四象限的 的概率是.
-
10、某同学用纸剪出了三种多边形,为凸四边形,凸五边形, 凸六边形, 每种至少剪出一个, 剪出的多边形边数之和为 111 , 那么剪出的多边形的所有内角中,直角的个数最多是.
-
11、如图,在矩形 中,点 是边 上的一动点, 连结 ,将线段 绕着点 顺时针旋转 ,得到 ,连结 ,交 于点 ,若 ,则 长的最大值为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、小明和爸爸计划从家出发去游泳馆,上午 8 点整小明先出发, 以 60 米/分的速度匀速步行, 途中不休息, 爸爸在上午 9 点 10 分从家出发, 沿同一路线, 以 300 米/分的速度匀速骑行到游泳馆, 每骑 5 分钟后休息 1 分钟, 最后, 爸爸比小明晚 5 分钟到达游泳馆,那么家距离游泳馆有( )A、4500 米 B、5100 米 C、5600 米 D、6000 米
-
13、已知实数 ,满足 ,则代数式 的值是 ( )A、 B、 C、3 D、
-
14、正方形 中,点 是 的中点,点 是 上异于点 的点, ,则 的值是( )
 A、1 B、 C、 D、
A、1 B、 C、 D、 -
15、如图是七巧板图案,现将它剪拼成一个“风筝”造型, 过它的上下左侧五点作矩形 ,点 为 的中点,并且在矩形内右上角有一正方形 ,若点 在同一直线上,点 到 的距离与到 的距离相等,且 ,则 的长为 ( )

 A、 B、 C、 D、
A、 B、 C、 D、 -
16、已知实数 满足 ,则 的取值范围是( )A、 B、 C、 D、
-
17、如图,在 中, 为 的中点, ,则 的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、若证明命题: “对于任意实数 恒成立”是假命题,只需要举一个反例,则这个反例可以是( )A、 B、 C、 D、
-
19、 都是实数,且 ,则 之间的大小关系是 ( )A、 B、 C、 D、
-
20、如图,点 为 外一点,过点 作 的两条切线,切点分别为 . 过点 作 的平行线交 于点 . 连结 交 于点 . 连结 并延长交 于点 . 求证: .
