-
1、如图,AD,BE是等边三角形ABC的两条角平分线,AD,BE相交于点O。求∠AOB的度数。

-
2、已知等腰三角形的顶角是底角的2倍,求这个三角形各内角的度数。
-
3、 已知:如图,在△ABC中,AB=AC,P为BC的中点,D,E分别为AB,AC上的点,且AD=AE。求证:PD=PE。先将分析的思路表示在下图中,再写出证明过程。
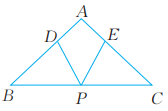
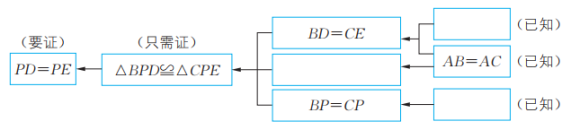
-
4、 如图,在△ABC中,AB=AC,∠ACD=100°,则∠A的大小为。
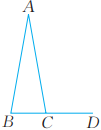
-
5、求证:等腰三角形两底角的平分线相等。
-
6、求等边三角形ABC三个内角的度数。
-
7、 已知:如图,∠B=∠E=90°,AB=AE,∠1=∠2。求证:∠3=∠4。

-
8、 已知:如图,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,且AP=PC,AP⊥PC。求证:△ABP≌△PDC。
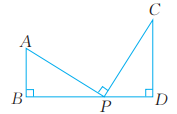
-
9、 具有下列条件的Rt△ABC与Rt△A'B'C'(其中, 是否全等?如果全等,写出理由。(1)、 AC=A'C',∠A=∠A';(2)、 AC=A'C',BC=B'C';(3)、∠A=∠A',∠B=∠B';(4)、 AB=A'B',∠B=∠B';(5)、
-
10、已知△ABC(如图),用直尺和圆规作一点P,使它到三边的距离都相等(只要求作出图形,并保留作图痕迹)。
-
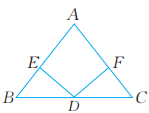
11、 已知:如图,在△ABC中,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF。求证:AB=AC。
-
12、已知:如图,P是∠AOB内一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE。求证:点P在∠AOB的平分线上。

-
13、已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=90°,BC=a,AB=c。

-
14、如图,中,、的角平分线、交于点P,延长、、 , , 则下列结论中正确的个数( )
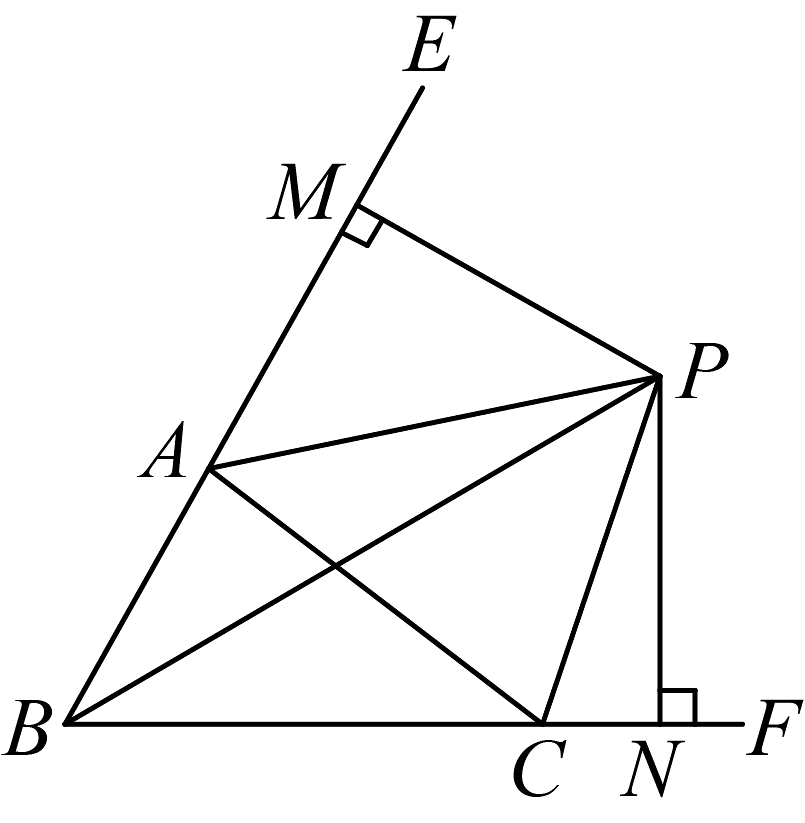
①平分; ②;③;④
A、1个 B、2个 C、3个 D、4个 -
15、下列相似图形不是位似图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
16、蓝山县供销超市用6000元购进一批“红富士”苹果进行试销,由于销售状况良好,超市又调拨13000元资金购进该品种苹果,但这次的进价比试销时的进价每千克多了0.5元,购进苹果的质量是试销时的2倍.试销时该品种苹果的进价是每千克多少元?
-
17、如图,是的边上的高,平分 , 若 , , 求和的度数.

-
18、解分式方程:(1)、(2)、 .
-
19、计算:
-
20、计算: .