-
1、
确定圆的条件
不在同一条直线上的三个点确定一个圆
三角形的外心
三角形三条边的的交点，即为三角形外接圆的圆心
防错提醒
锐角三角形的外心在三角形的内部，直角三角形的外心为直角三角形的斜边中点，钝角三角形的外心在三角形的外部
-
2、
圆
在同一平面内，线段 OP 绕它固定的一个端点O 旋转一周，另一端点 P 所经过的封闭曲线叫做圆.定点O叫做圆心，线段OP 叫做圆的半径
弦
连结圆上任意两点的叫做弦
直径
经过圆心的弦叫做直径
弧
圆上任意两点间的部分叫做圆弧，简称弧
半圆
圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆
优弧
大于半圆的弧叫做优弧
劣弧
小于半圆的弧叫做劣弧
-
3、 问题情境：
如图①，在正方形ABCD中，点E，F分别在边 BC，CD 上，且 AE⊥BF，垂足为 M，那么 AE 与BF 相等吗?
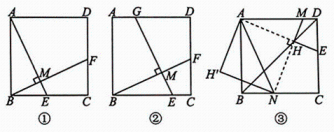(1)、直接判断：AE BF（填“=”或“≠”）；在“问题情境”的基础上，继续探索：(2)、问题探究：如图②，在正方形ABCD中，点E，F，G分
别在边 BC，CD 和 DA 上，且 GE⊥BF，垂足为M，那么 GE 与 BF 相等吗?请证明你的结论；
(3)、问题拓展：如图③，点 E在边 CD 上，且 MN⊥AE，垂足为H，当点 H在正方形ABCD 的对角线BD上时，连结AN，将△AHN沿AN 翻折，点 H落在点 H'处.四边形AHNH'是正方形吗?请说明理由.
-
4、 如图，已知正方形ABCD的边长为5，点E，F分别在AD，DC上，AE=DF=2，BE与AF 相交于点G，H 为BF 的中点，连结GH，则GH 的长为.
-
5、 如图，在正方形ABCD中，点E，F分别在边CD，AD 上，BE⊥CF于点G，若BC=8，AF=2，则GF的长为.
-
6、如图，在正方形ABCD中，E，F分别为边BC，CD的中点，连结AE，BF交于点P，连结CP 并延长，交 AB 于点Q.
求证：
(1)、PC平分∠EPF；(2)、AQ=2BQ. -
7、如图，在正方形ABCD中，E，F分别为边BC，CD的中点，连结 AE，BF交于点 P，连结 PD.求证：
(1)、AE⊥BF；(2)、PD=AB. -
8、已知：如图，在正方形ABCD中，E，F 分别是BC，CD 上的点，AE⊥BF.求证：AE=BF.
-
9、 如图
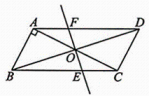
【感知】如图①，在▱ABCD中，对角线 AC，BD 相交于点O，过点O的直线EF 分别交边 AB，CD 于点E，F.易证：△BOE≌△DOF（不需要证明）.
【探究】若图①中的直线 EF 分别交边 CB，AD的延长线于点H，G，其他条件不变，如图②.求证：△BOH≌△DOG；
【应用】在图②中，连结 AH.若∠ADB=90°，AB=10，AD=6，BH= BC，求 GH 的长和四边形AHBD 的面积.
-
10、 如图，在▱ABCD 中，过对角线 AC的中点 O作直线 EF 交边 AB，CD于点E，F.
(1)、求证：AE=CF；(2)、若EF⊥AC，AC=8，cos∠BAC=0.8，连结AF，CE，求四边形AECF 的面积. -
11、 如图， □ABCD的对角线AC，BD相交于点O，E 为边 BC 的中点，连结 EO 并延长交边AD 于点F，∠ABC=60°，BC=2AB.下列结论错误的是（ ）
A、AB⊥AC B、AD=4OE C、四边形 AECF 为菱形 D、 -
12、 如图，O是菱形ABCD 的对称中心，连结OA，OB，OA=4，OB=6，EF为过点O 的一条直线，点E，F分别在AD，BC上，则图中阴影部分的面积为（ ）
A、24 B、16 C、18 D、12 -
13、如图5，在□ABCD 中，AB⊥AC，AB=1，BC= 对角线AC，BD 相交于点O，将直线 AC 绕点 O 顺时针旋转，分别交 BC，AD于点E，F.
(1)、【问题解决】求证：当旋转角为90°时，四边形ABEF是平行四边形.
(2)、【类比探究】试说明在旋转过程中，线段 AF 与EC 总保持相等.
(3)、【拓展应用】在旋转过程中，四边形BEDF 可能是菱形吗?如果不可能，请说明理由；如果可能，请证明并求出此时AC绕点O 顺时针旋转的度数.
-
14、如图， □ABCD 的对角线AC，BD 相交于点O，EF 过点O 且分别与AB，CD交于点E，F，连结 EC.
(1)、求证：OE=OF；(2)、若EF⊥AC，△BEC的周长是10，求□ABCD的周长. -
15、如图，EF过▱ABCD 对角线的交点O，交AD 于点E，交 BC于点 F，有下列结论：①AE=CF；②若AB=4，AC=6，则 2<BD<14；③S△AOB = S□ABCD；（；④S四边形ABFE=S△ABC.其中正确的结论是.（只填序号）
-
16、已知：如图， ▱ABCD的对角线AC，BD交于点O.过点O作直线EF，分别交AB，CD于点E，F.求证：OE=OF.
-
17、已知正方形 ABCD，E 是对角线 AC 上一点.
(1)、 如图①，连结 BE， DE，求证：△ABE≌△ADE；(2)、如图②，F 是 DE 延长线上一点，DF 交AB 于点G，BF⊥BE.判断△FBG的形状，并说明理由；(3)、在（2）的条件下，若BE=BF=2，求 的值. -
18、 如图，在▱ABCD中，对角线AC，BD相交于点O，∠ABC=90°.
(1)、求证：AC=BD；(2)、点 E 在 BC 边上，满足∠CEO=∠COE.若AB=6，BC=8，求 CE 的长及 tan∠CEO的值. -
19、如图，矩形 ABCD 的对角线 AC与 BD 相交于点 O，OE∥CD，直线CE是线段 OD 的垂直平分线，CE 分别交 OD，AD 于点 F，G，连结 DE.
(1)、判断四边形OCDE 的形状，并说明理由；(2)、当CD=4时，求 EG的长. -
20、如图，在 Rt△ABC中，∠BAC=90°，D 是 BC 的中点，E 是 AD 的中点，过点 A 作AF∥BC交CE的延长线于点F，连结BF.
(1)、求证：四边形ADBF是菱形；(2)、若AB=8，四边形ADBF的面积为32 点 M 在线段BC 上，AM=7，求 BM的长.