相关试卷

1、若关于 $x$ 的一元一次方程 $\frac{1}{2025} x + 3 = 2 x + b$ 的解为 $x = - 3$ ，则关于 $y$ 的一元一次方程 $\frac{1}{2025} (2 y + 1) = 4 y + b - 1$ 的解为（）

A、 $y = 1$ B、 $y = - 1$ C、 $y = - 2$ D、 $y = - 4$

查看解析
2、下列变形正确的是（）

A、若 $a x = a y$ ，则 $x = y$ B、若 $a = b$ ，则 $a + c = b - c$ C、若 $a = b$ ，则 $\frac{a}{c} = \frac{b}{c}$ D、若 $x = y$ ，则 $x + 2 m = y + 2 m$

查看解析
3、我国古代著作《增删算法统宗》中有这样一道题，其大意是：“孩童们在庭院玩耍，不知有多少人和梨．每人分4个梨，多12个梨；每人分6个梨，恰好分完．”设孩童有x名，则可列方程为（）

A、 $\frac{x}{4} + \frac{x}{6} = 12$ B、 $\frac{x}{4} - 12 = \frac{x}{6}$ C、 $4 x - 12 = 6 x$ D、 $4 x + 12 = 6 x$

查看解析
4、若 $3 m^{2 x} n^{5}$ 与 $- 7 m^{4} n^{y + 1}$ 是同类项，则（）

A、 $x = 2$ ， $y = 2$ B、 $x = 2$ ， $y = 4$ C、 $x = \frac{5}{2}$ ， $y = 4$ D、 $x = \frac{5}{2}$ ， $y = 3$

查看解析
5、下列方程是一元一次方程的是（）

A、 $2 x - 1 = 0$ B、 $3 x - 2 y = 1$ C、 $x^{2} = 4$ D、 $\frac{1}{x} - 2 = 3$

查看解析
6、如图，O是等边三角形ABC内一点.将△BOC绕点C按顺时针方向旋转60°得到△ADC，连接OD.已知∠AOB=110°.

(1)、求证：△COD是等边三角形.

(2)、当α=150°时，试判断△AOD的形状，并说明理由.

(3)、探究：当α为多少度时，△AOD是等腰三角形?

查看解析
7、台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力.如图，有一台风中心沿东西方向AB由点A向点B移动，已知点C为一海港，且点C与直线AB上两点A，B的距离分别为300 km和400 km，又AB=500 km，以台风中心为圆心周围250 km以内为受影响区域.

(1)、海港C受台风影响吗?为什么?

(2)、若台风的速度为20 km/h，台风影响该海港持续的时间有多长?

查看解析
8、如图，在△ABC中，∠C=90°，点P，D分别在AC，AB上，且PD=PA，BD的垂直平分线交BC于点E，交BD于点F，连接PE，DE.

(1)、求证：DE⊥PD.

(2)、若AC=10，BC=12，PA=3，求线段DE的长.

查看解析
9、如图，在△ABC中，AB=AC，点D为AC上一点，且满足AD=BD=BC.点F在BC延长线上，连接FD并延长，交AB于点E，连接AF.

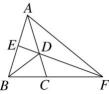(1)、求∠BAC和∠ACB的度数.

(2)、若点E是AB的中点，求证：△ABF是等腰三角形.

查看解析
10、如图，DE⊥AB于点E，DF⊥AC于点F，若BD=CD，BE=CF.
求证：AD平分∠BAC.

查看解析
11、如图，在△ABC中，AB=AC，D是BC边上的中点，连接AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F.

(1)、若∠C=36°，求∠BAD的度数.

(2)、求证：FB=FE.

查看解析
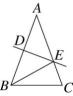
12、如图，在△ABC中，AB=AC，DE是AB的垂直平分线，垂足为D，交AC于点E，已知∠ABE=40°，求∠EBC的度数.

查看解析
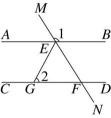
13、如图，AB∥CD，直线MN与AB，CD分别交于点E，F，CD上有一点G且GE=GF，∠1=122°，求∠2的度数.

查看解析
14、如图所示的是某超市购物车的侧面简化示意图.测得支架AC=24cm，CB=18cm，两轮中心的距离AB=30cm，则点C到AB的距离为 cm.

查看解析
15、如图，在△ABC中，点D在边BC上，AB=AD，E，F分别是AC，BD的中点，EF=3，则AC的长为.

查看解析
16、如图，AB∥CD，∠C=33°，OC=OE，则∠A=°.

查看解析
17、如图，3×3网格由9个边长为1的小正方形组成，以点B为圆心，AB长为半径画圆弧交数轴于点A'，则点A'表示的实数为( )

A、- $\sqrt{5}$ B、 $\sqrt{5}$ C、-2 $\sqrt{5}$ D、- $\sqrt{5}$ +1

查看解析
18、如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交AC于点M，P是直线MN上一动点，点H为BC的中点.若BC=6，△ABC的面积是24，则PB+PH的最小值为( )

A、5 B、8 C、12 D、24

查看解析
19、如图，在Rt△ABC中，D是AC的中点，∠BDC=60°，AC=6，则BC的长是( )

A、3 B、6 C、 $\sqrt{3}$ D、3 $\sqrt{3}$

查看解析
20、如图，点C，E在OA上，点D在OB上，且OC=CD=DE，若∠EDB=75°，则∠AOB=( )

A、35° B、25° C、20° D、15°

查看解析

上一页 606 607 608 609 610 下一页跳转