相关试卷

1、大自然是美的设计师，即使是一个小小的盆景，经常也会产生最具美感的黄金分割比例．如图，点 $B$ 为 $A C$ 的黄金分割点，即 $A B^{2} = B C \cdot A C$ ．若 $A C = 20 cm$ ，则 $B C$ 的长为 $cm$ ．

查看解析
2、如图在 $△ A B C$ 中， $A B$ 的垂直平分线 $D E$ 分别交 $B C$ 、 $A B$ 于点 $D$ 、点 $E$ ，连接 $A D$ ．若 $A E = 5 cm$ ， $△ A C D$ 的周长为 $16 cm$ ，则 $△ A B C$ 的周长为 $cm$ ．

查看解析
3、如图，某单位拟在一块空地上修建矩形植物园 $A B C D$ ，其中一边靠墙，可利用的墙长不超过 $16$ 米，另外三边由 $40$ 米长的栅栏围成，设矩形 $A B C D$ 中，垂直于墙的边 $A B = x$ 米，面积为y平方米．

(1)、若矩形 $A B C D$ 的面积为 $150$ 平方米，求x的值；

(2)、当矩形 $A B C D$ 的面积最大时，利用的墙长是多少米？并求此时的最大面积．

查看解析
4、解答下列各题

(1)、如图，在 $∠ A O B$ 中，以 $O$ 为顶点引射线，填表：
$∠ A O B$ 内射线的条数
$1$
$2$
$3$
$4$
角的总个数
______
______
______
_____

(2)、若 $∠ A O B$ 内射线的条数是 $n$ ，请用关于 $n$ 的式子表示出上面的结论．

(3)、若 $∠ A O B$ 内有射线条数是 $2024$ ，则角的总个数为多少？

查看解析
5、已知等腰三角形一边长为4，另两边恰好是关于 $x$ 的方程 $x^{2} - (m + 1) x + 2 (m - 1) = 0$ 的根，求此三角形的另两边长．

查看解析
6、解方程：

(1)、 ${(x - 3)}^{2} + 2 x (x - 3) = 0$ ；

(2)、 $x^{2} - 4 x + 1 = 0$

查看解析
7、已知一个三角形的两条直角边的长恰好是方程 $2 x^{2} + k x + 7 = 0$ 的两个根，且这个直角三角形的斜边上的中线长是 $\frac{3}{2}$ ，则k的值是（）

A、8 B、 $- 8$ C、8或 $- 8$ D、4或 $- 4$

查看解析
8、一元二次方程 $x^{2} - x - 1 = 0$ 的二次项系数和一次项系数分别是（）

A、 $0, - 1$ B、 $1, - 1$ C、0，1 D、 $- 1, - 1$

查看解析
9、如图， $△ A B C$ 中， $D$ 为 $B C$ 的中点，连接 $A D$ 并延长到 $E$ ，使 $D E = A D$ ．求证： $A C ∥ B E$ ．

查看解析
10、如图，在△ABC中，AB=AC，∠BAC=90°，BC=12厘米．过点C作直线 $l ⊥ B C$ ，动点P从点C开始沿射线CB方向以2厘米/秒的速度运动，动点Q也同时从点C出发在直线 $l$ 上以1厘米/秒的速度向上或向下运动．连接AP、AQ，设运动时间为t秒．
（1）请写出CP、CQ的长度（用含t的代数式表示）：CP= 厘米，CQ= 厘米；
（2）当点P在边BC上时，若△ABP的面积为24厘米 $^{2}$ ，求t的值；
（3）当 $t$ 为多少时，△ABP与△ACQ全等？

查看解析
11、如图，点E在△ABC的中线AD的延长线上，且DE＝AD．
（1）求证：BE＝AC；
（2）若AB＝3，AC＝7，求AD的取值范围．

查看解析
12、如图， $A B = A C$ ， $B D = C D$ ， $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ．求证： $D E = D F$ ．

查看解析
13、某学校组织学生乘车赴红色教育基地——红旗渠参观，若全部租用7座的车需要x辆，且最后一辆车还差2人未坐满，则该校学生一共有人．

查看解析
14、在古希腊时期，有一天毕达哥拉斯走在街上，在经过铁匠铺前他听到铁匠打铁的声音非常好听，于是驻足倾听，他发现铁匠打铁节奏很有规律，这个声音的比例被毕达哥拉斯用数学的方式表达出来，后来人们将这个数 $\frac{\sqrt{5} - 1}{2}$ 称为黄金分割数．设 $a = \frac{\sqrt{5} - 1}{2}, b = \frac{\sqrt{5} + 1}{2}$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ ， $S_{3} = \frac{1}{1 + a^{3}} + \frac{1}{1 + b^{3}} \dots$ ， $S_{100} = \frac{1}{1 + a^{100}} + \frac{1}{1 + b^{100}}$ ，则 $S_{1} + S_{2} + S_{3} + \dots + S_{100}$ 的值为（）

A、 $100 \sqrt{5}$ B、 $200 \sqrt{2}$ C、100 D、505

查看解析
15、在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， D为边 $A B$ 上一点．

(1)、如图1，若 $A C = \sqrt{72}$ ， $A D = 3$ ，求 $△ C D B$ 的面积；

(2)、如图2，作 $D E ⊥ C D$ ，且 $D E = C D$ ，连结 $C E$ 交边 $A B$ 于点F，连结 $B E$ ．
①若 $B C = B D$ ，求证： $∠ A D C = ∠ B E D$ ；
②若 $B D > B C$ ，写出线段 $B C$ ， $B E$ ， $C E$ 长度之间的等量关系，并说明理由．

查看解析
16、如图，在 $△ A B C$ 中， $A D ⊥ B C$ ，于点D，E为 $A C$ 上一点，连结 $B E$ ．

(1)、若 $B F = A C$ ， $D F = D C$ ．
①求证： $△ A D C ≌ △ B D F$ ；
②若 $∠ A B E = 25 °$ ，求 $∠ C A D$ 的度数；

(2)、若 $∠ A B E = ∠ D A C$ ， $B E ⊥ A C$ ， $A B = 13$ ， $C E = 5$ ，求 $C D$ ．

查看解析
17、在 $△ A B C$ 中， $A D ⊥ B C$ ， $E$ 是 $B C$ 上的一点．

(1)、若E是 $B C$ 的中点， $A B = 10$ ， $A D = 6$ ， $∠ C = 45 °$ ，求 $A E$ 的长；

(2)、若 $A E$ 是 $∠ B A C$ 的角平分线， $∠ B = 40 °$ ， $∠ C = 60 °$ ，求 $∠ E A D$ 的度数．

查看解析
18、如图， $A D$ 是 $△ A B C$ 的角平分线， $∠ C = 90 °$ ， $C D = 1cm$ ，点P是 $A B$ 上一动点．

(1)、连接 $D P$ ，求 $D P$ 的最小值；

(2)、若 $∠ B = 30 °$ ，求 $△ A D B$ 的面积．

查看解析
19、如图，在正方形网格中点A，B，C均为格点，按要求作图（保留作图痕迹，不写作法）：

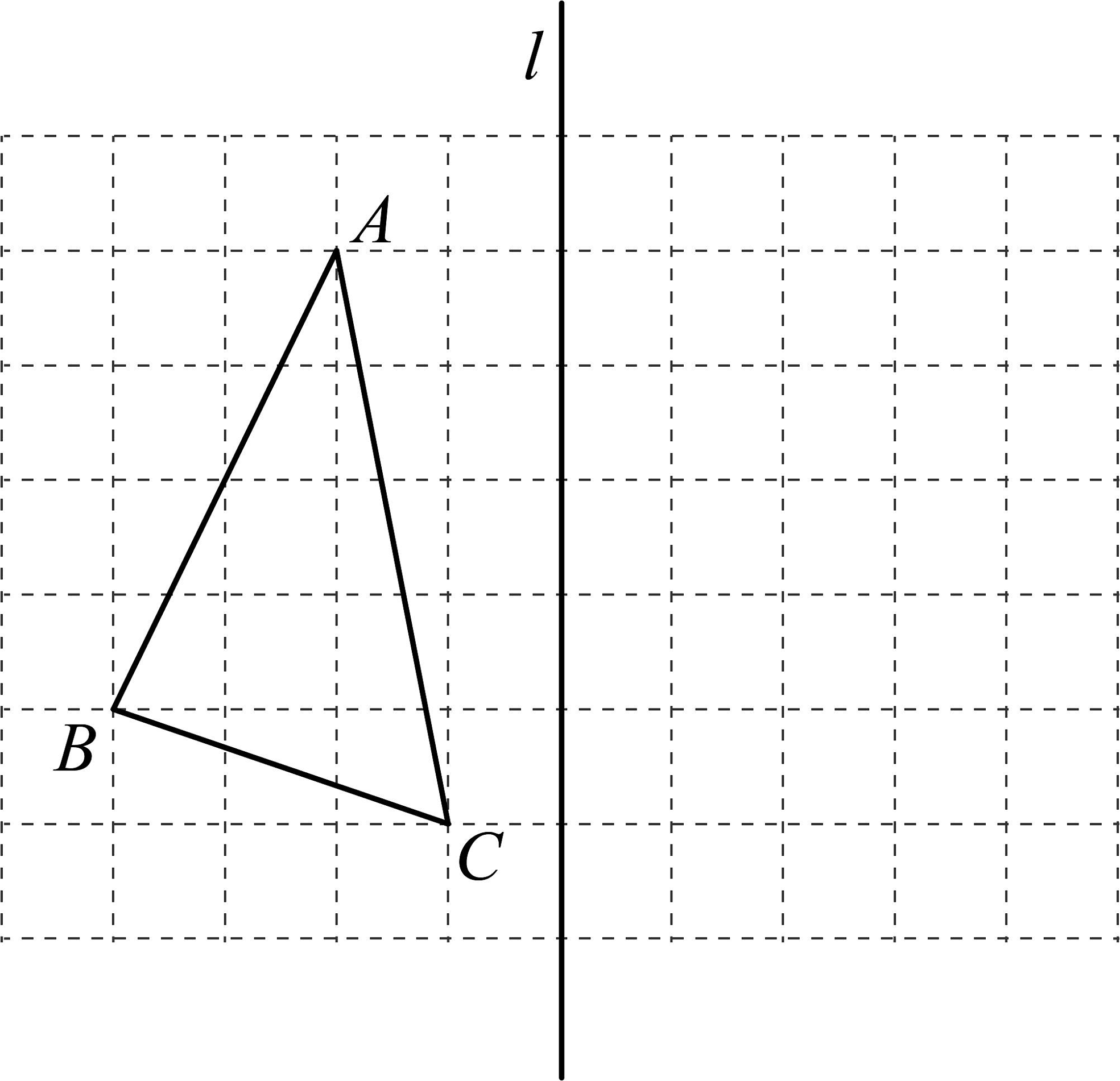(1)、作出 $△ A B C$ 关于直线l的对称图形 $△ A^{'} B^{'} C^{'}$ ；

(2)、求 $△ A B C$ 的面积；

(3)、在直线l上找一点D，使 $A D + C D$ 最小．

查看解析
20、如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点 $D$ ， $E$ 分别在 $A C$ ， $B C$ 上，且 $∠ C D E = ∠ B$ ，将 $△ C D E$ 沿 $D E$ 折叠，点 $C$ 恰好落在 $A B$ 边上的点 $F$ 处， $C F$ 与 $D E$ 交于点 $G$ ．下列结论：其中正确的结论有．（填序号）
$①$ $A B = 2 C F$ ；
$②$ 若 $∠ A B C = 50 °$ ，则 $∠ A F D = 60 °$ ；
$③$ 若 $C D = 1.5$ ， $C E = 2$ ，则 $D G \cdot G E = 1.2$ ；
$④$ 若 $A C = 4$ ， $B C = 3$ ，则 $C G = 1.25$ ．

查看解析

上一页 537 538 539 540 541 下一页跳转

$∠ A O B$ 内射线的条数	$1$	$2$	$3$	$4$
角的总个数	______	______	______	_____