-
1、 计算: .
-
2、 在矩形中, , , , 分别是边 , 的中点,于点 , 的延长线交于点 , 则的长是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、 如图,在中, , 点E是中点,作于点F , 已知 , , 则的长为( )
 A、1.2 B、2.4 C、3.6 D、0.6
A、1.2 B、2.4 C、3.6 D、0.6 -
4、 如图,在菱形中,对角线与相交于点O , , 垂足为E , 若 , 则的大小为( )
 A、33度 B、34度 C、57度 D、67度
A、33度 B、34度 C、57度 D、67度 -
5、 若a , b为实数,且 , 则的平方根是( )A、36 B、6 C、 D、
-
6、 已知点在第二象限,则一次函数的图象可能是( )A、
 B、
B、 C、
C、 D、
D、
-
7、 在平面直角坐标系中,点关于原点对称的点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
8、 下列方程中是关于x的一元二次方程的是( )A、 B、 C、 D、
-
9、 如图是上海今年春节七天最高气温()的统计结果,这七天最高气温的众数和中位数是( )
 A、15,17 B、17,17 C、17,14 D、17,15
A、15,17 B、17,17 C、17,14 D、17,15 -
10、 若分式的值为0,则的值为( )A、 B、 C、 D、
-
11、 如图,已知抛物线与x轴交于A、B两点,过点A的直线l与抛物线交于点C , 其中A点的坐标是 , C点坐标是 .
 (1)、求抛物线解析式;(2)、点G是(1)中抛物线对称轴上的动点,点F是x轴上的动点,点M是(1)中抛物线上的一动点且位于直线上方.当面积最大时,求的最小值.(3)、将(1)中抛物线沿射线平移个单位长度得到新的抛物线 , 点K为新抛物线上一点,使得 . 请直接写出所有满足条件的点K的横坐标.
(1)、求抛物线解析式;(2)、点G是(1)中抛物线对称轴上的动点,点F是x轴上的动点,点M是(1)中抛物线上的一动点且位于直线上方.当面积最大时,求的最小值.(3)、将(1)中抛物线沿射线平移个单位长度得到新的抛物线 , 点K为新抛物线上一点,使得 . 请直接写出所有满足条件的点K的横坐标. -
12、 阅读下列材料:在苏科版九年级数学上册第页,我们把就叫做一元二次方程根的判别式,我们用表示,即 . 如果的值是一个完全平方数时,一元二次方程的根不一定都为整数,但是如果一元二次方程的根都为整数,的值一定是一个完全平方数.
例如:方程 , , 的值是一个完全平方数,但是该方程的根为 , 不都为整数;方程的两根 , 都为整数,此时 , 的值是一个完全平方数.我们定义:两根都为整数的一元二次方程称为“全整根方程”,代数式的值为该“全整根方程”的“关爱码”,用表示,即;若另一关于x的一元二次方程也为“全整根方程”,其“关爱码”记为 , 当满足时,则称一元二次方程是一元二次方程的“全整根伴侣方程”.
(1)、关于x的一元二次方程是一个“全整根方程”.①当时,该全整根方程的“关爱码”是 .
②若该全整根方程的“关爱码”是 , 则m的值为 .
(2)、关于x的一元二次方程(m为整数,且)是“全整根方程”,请求出该方程的“关爱码”.(3)、若关于x的一元二次方程是(m , n均为正整数)的“全整根伴侣方程”,求的值(直接写出答案). -
13、 已知:如图一次函数与轴相交于点 , 与轴相交于点 , 与轴相交于点 , 这两个函数图象相交于点 .
 (1)、求出 , 的值;(2)、求的面积.(3)、在轴上是否存在点 , 使得为等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求出 , 的值;(2)、求的面积.(3)、在轴上是否存在点 , 使得为等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由. -
14、 某商家销售一种成本为20元的商品,销售一段时间后发现,每天的销量y(件)与当天的销售单价(元)满足一次函数关系,并且当时,;当时, . 物价部门规定,该商品的销售单价不能超过45元.(1)、求y关于的函数关系式;(2)、当销售单价定为多少元时,商家销售该商品每天获得的利润是8000元?(3)、求商家销售该商品每天获得的最大利润.
-
15、 如图,将矩形的边延长到点 , 使 , 连接、 , 作交延长线于点 , 连接 .
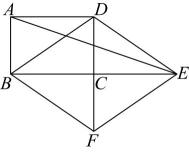 (1)、求证:四边形为菱形;(2)、如果四边形的面积为24, , 连接 , 求的长.
(1)、求证:四边形为菱形;(2)、如果四边形的面积为24, , 连接 , 求的长. -
16、 已知关于x的一元二次方程 .(1)、若方程有实数根,求m的取值范围;(2)、是否存在实数m , 使方程的两根 , 满足?若存在,求出实数m的值;若不存在,请说明理由.
-
17、 某公司为参加“2025年中国人形机器人生态大会”,对本公司生产的甲、乙两款人形机器人的满意度进行了评分测验,并从中各随机抽取20份对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:A: , B: , C: , D:)下面给出了部分抽取的信息:
对甲款机器人的评数据中B等级的数据为:90,90,88,88,88,87,86,85.
对乙款机器人的评分数据为:64,70,75,76,78,78,85,85,85,85,86,89,90,90,94,95,98,98,99,100.
对甲,乙两款机器人的满意度评分统计表:
机器人
平均数
中位数
众数
方差
甲
86
86.5
88
69.8
乙
86
85.5
a
96.6
对甲款机器人的满意度评分扇形统计图:
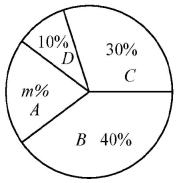
根据以上信息,解答下列问题:
(1)、上述图表中 , .(2)、根据以上数据,你认为哪款机器人的满意度更好?请说明理由(写出一条理由即可)(3)、在此次测验中,各有800人对甲、乙两款人形机器人进行评分,估计此次测验中甲、乙两款人形机器人的满意度评分为A等级的共有多少人? -
18、 解方程(1)、(2)、
-
19、 计算: .
-
20、 已知点 , (点A在点B的左侧)是抛物线上的两点,若 , 则与满足的条件是 .