-
1、计算:|﹣3|2sin30°.
-
2、定义:在平面直角坐标系中,到原点的距离等于1的点叫做“单位圆点”.
⑴下列三个函数的图象上存在“单位圆点”的是 (填番号);
①y=x+2;
②y;
③y=x2+1.
⑵若一次函数yx+m的图象上存在“单位圆点”,则m的取值范围为 .
-
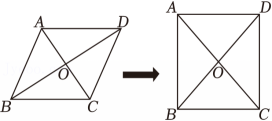
3、如图,在▱ABCD中,对角线AC与BD相交于点O.小乐同学欲添加两个条件使得四边形ABCD是正方形,现有三个条件可供选择:①AC⊥BD;②AC=BD;③∠ADC=90°.则正确的组合是 (只需填一种组合即可).
-
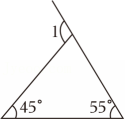
4、如图,∠1的度数为 .
-
5、某校举行演讲比赛,5位评委对某选手给出的评分如下:7.5,7.5,7,7.5,8,则评分的众数为 .
-
6、已知二次函数y=x2+4x+m的图象经过A(x1 , y1)、B(x2 , y2)两点,有下列结论:
①二次函数的图象开口向上,对称轴为直线x=﹣2;
②当m<4时,二次函数的图象与x轴有两个交点;
③若y1<y2 , 则|x1+2|>|x2+2|;
④当x≥﹣2时,二次函数的图象与y=2x﹣1的图象有两个交点,则﹣1≤m<0.
其中,正确的结论有( )
A、1个 B、2个 C、3个 D、4个 -
7、醇是一类由碳、氢、氧元素组成的有机化合物,如图是这类物质前四种化合物的分子结构模型图,其中
 代表碳原子,
代表碳原子, 代表氧原子,〇代表氢原子.第1种如图1有4个氢原子,第2种如图2有6个氢原子,第3种如图3有8个氢原子,第4种如图4有10个氢原子,……按照这一规律,第9种化合物的分子结构模型中氢原子的个数是( )
代表氧原子,〇代表氢原子.第1种如图1有4个氢原子,第2种如图2有6个氢原子,第3种如图3有8个氢原子,第4种如图4有10个氢原子,……按照这一规律,第9种化合物的分子结构模型中氢原子的个数是( )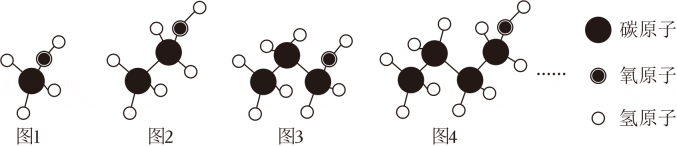 A、18 B、20 C、22 D、24
A、18 B、20 C、22 D、24 -
8、某学校食堂有7元、8元和9元三种价格的午餐供师生选择(每人限定一份),5月份销售情况如图所示,则师生购买午餐的平均价格为( )
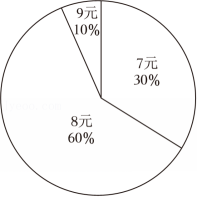 A、7.8元 B、7.9元 C、8元 D、8.1元
A、7.8元 B、7.9元 C、8元 D、8.1元 -
9、若方程x2﹣x﹣2=0的两个根是x1和x2 , 则x2+x1的值为( )A、﹣1 B、1 C、﹣2 D、2
-
10、如图,l1∥l2∥l3 , AB=2,DE=3,BC=4,则EF的长为( )
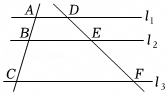 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10 -
11、计算:的结果为( )A、 B、 C、﹣1 D、1
-
12、如图,在平面直角坐标系中,点P的坐标是( )
 A、(﹣3,﹣2) B、(﹣3,2) C、(3,2) D、(3,﹣2)
A、(﹣3,﹣2) B、(﹣3,2) C、(3,2) D、(3,﹣2) -
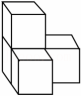
13、如图是由4个相同的正方体堆成的物体,则它的俯视图是( )
 A、
A、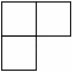 B、
B、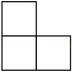 C、
C、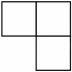 D、
D、
-
14、如图,两条平行线a、b被第三条直线c所截.若∠1=70°,则∠2=( )
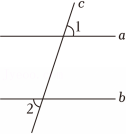 A、130° B、110° C、90° D、70°
A、130° B、110° C、90° D、70° -
15、2025年“五一”期间,乐山大佛“夜游凌云山”项目营收突破300万元,创下同期历史新高.数据3000000用科学记数法表示为( )A、3×105 B、3×106 C、3×107 D、3×108
-
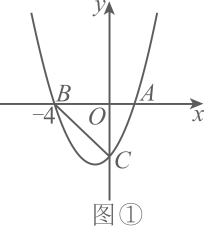
16、在平面直角坐标系中,抛物线()与轴交于点和点 , 与轴交于点 .(1)、求与的关系;(2)、如图①,当时,点在抛物线上, , 求点的坐标;
 (3)、如图②,若抛物线上一点关于直线的对称点是的外心 , 求的值.
(3)、如图②,若抛物线上一点关于直线的对称点是的外心 , 求的值.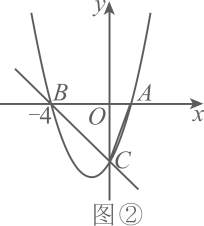
-
17、综合与实践(1)、【初步感知】如图①,和中, , , , 求的度数;
 (2)、【深入探究】如图②,在矩形中, , 点E是线段上一点,连接 , 过点A在上方作 , 使 , 连接 , 请证明 , 并直接写出点F到的距离的最大值;
(2)、【深入探究】如图②,在矩形中, , 点E是线段上一点,连接 , 过点A在上方作 , 使 , 连接 , 请证明 , 并直接写出点F到的距离的最大值;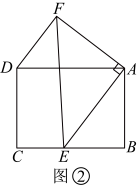 (3)、【学以致用】如图③,梯形中, , , , , 点E是线段的中点,点F是线段上一点,连接 , 过点E在上方作 , 使 , 当的面积最小时,求的长.
(3)、【学以致用】如图③,梯形中, , , , , 点E是线段的中点,点F是线段上一点,连接 , 过点E在上方作 , 使 , 当的面积最小时,求的长.
-
18、如图,是的直径,点D是线段延长线上一点,过点D的直线与相切于点C,过线段上一点E作的垂线交的延长线于点F,交于点G.
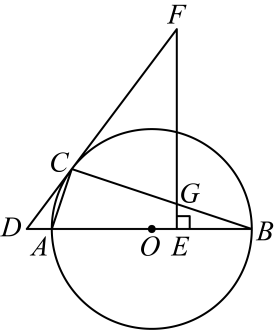 (1)、求证:;(2)、若 , 求的长.
(1)、求证:;(2)、若 , 求的长. -
19、如图,在平面直角坐标系中,一次函数的图象分别与x轴,y轴交于点A,点C,与反比例函数的图象交于点 .
 (1)、求一次函数和反比例函数的表达式;(2)、点是反比例函数图象上一点,连接 , 求的面积;(3)、点P在y轴上,满足是以为斜边的直角三角形,请直接写出点P的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、点是反比例函数图象上一点,连接 , 求的面积;(3)、点P在y轴上,满足是以为斜边的直角三角形,请直接写出点P的坐标. -
20、某校开展阳光体育大课间活动,需购买一批球类用品.在采购中发现,篮球的单价比足球的单价高20元,用10000元购买篮球的数量和用8000元购买足球的数量相同.(1)、求篮球和足球的单价;(2)、学校需购买篮球和足球共120个(两种球都要购买),足球的数量不能多于篮球数量的 , 设购买篮球x个,总费用为y元,求总费用y(元)与x(个)的函数关系式,并求出x的取值范围和总费用最低时的购买方案.