相关试卷

1、如图，∠AOB=60°，射线OP 从OA 开始绕点O以每秒10°的速度逆时针旋转，同时射线OQ 从OB 开始绕点O以每秒6°的速度逆时针旋转.设旋转的时间为t 秒(0≤t≤36).

(1)、t 为何值时，OP 与OQ 重合?

(2)、t 为何值时，∠POQ=40°?

(3)、如图，∠AOC=50°，OM 平分∠AOP，若∠COM=20°，直接写出t 的值.

查看解析
2、已知∠AOB，射线OC 在∠AOB 内部，∠AOB 与∠BOC 互补，且∠AOB=5∠BOC.

(1)、求∠BOC，∠AOB 的度数；

(2)、如图1，射线OP 绕点O从OA 开始以15°/秒的速度顺时针旋转至 OC 停止转动，同时射线OQ 绕点O从OB 开始以3°/秒的速度逆时针旋转至OC 停止转动.设旋转时间为t秒，当∠POC=2∠QOC 时，求t 的值；

(3)、如图2，射线OC 绕点O以每秒12°的速度逆时针旋转，OM 平分∠AOC，同时，射线OE从OA 的位置出发往返于∠AOB 内，旋转速度为每秒15°，设旋转时间为t 秒，且0<t≤25，当∠EOM=50°时，t 的值为 .

查看解析
3、如图1，把一副三角尺拼在一起，其中直角顶点重合，三角形ABC 是等腰直角三角形，∠BCA=90°，并且B，C，E 三点在同一直线上.如图2，若射线( $C B^{'} ， C A^{'}$ 分别从CB，CA 位置开始，同时绕点 C 以每秒5°的速度顺时针匀速旋转( $α (0^{\circ} < α < 18 0^{\circ}) ，$ ， CF 平分 $∠ A^{'} C B ，$ CG 平分∠B'CE，设旋转的时间为t秒.当t为何值时， $∠ B^{'} C F = 2 ∠ G C A^{'} ?$

查看解析
4、

(1)、如图1，∠AOB=120°，∠COD=60°.试探究∠AOD 与∠BOC 的数量关系，并说明理由；

(2)、如图2，当∠COD 在∠AOB 的外部时，分别在∠AOC 内部和∠BOD 内部画射线OE，OF，使 $∠ E O C = \frac{1}{3} ∠ A O C ， ∠ D O F = \frac{1}{3} ∠ B O D ，$ 若∠EOF=80°，求证：∠AOB+2∠COD=240°.

查看解析
5、已知∠AOB=160°，∠COE=80°，OF 平分∠AOE.

(1)、如图1，若∠COF=14°，求∠BOE 的度数；

(2)、当射线OE 绕点O逆时针旋转到如图2的位置时，探究∠BOE 与∠COF 的数量关系，并说明理由.

查看解析
6、

(1)、“三角尺拼角”：将一副三角尺如图1这样放置，就可画出. $∠ A O B = 7 5^{\circ} ，$ 用一副三角尺还能画出其他特殊角.
①设计用一副三角尺画出105°角的画图方案，并画出相应的几何图形；
②用一副三角尺能画出145°的角吗? .(填“能”或“不能”).

(2)、如图2，现有19°，23°，29°角的三种模板， $∠ A B C = 1 9^{\circ} ， ∠ F E D = 2 3^{\circ} ， ∠ I H G = 2 9^{\circ} .$ 请设计一种方案，只用给出的一种模板画出1°的角.动手操作：如图3，M，O，N三点在一条直线上，将∠ABC 的顶点B 与点O 重合，BC 边与射线ON 重合，如图所示，将∠ABC 绕点O 逆时针旋转19°得∠A₁B₁C₁ ，再将∠A₁B₁C₁ 绕点O 逆时针旋转 19°得 $∠ A_{2} B_{2} C_{2} ， \dots ，$ 如此连续操作 18 次，再利用两个平角等于一个周角，可得1°的角，即： $1 9^{\circ} \times 19 - 18 0^{\circ} \times 2 = 36 1^{\circ} - 36 0^{\circ} = 1^{\circ} .$ 请从23°或29°角模板中选一个你认为能画出1°角的模板，设计一个方案，并说明理由.

查看解析
7、【感悟体验】如图1，A，B，C三点在同一直线上，点 D 在线段AC 的延长线上，且AB=CD，请仅用一把圆规在图中确定点 D 的位置.

(1)、【认识概念】在同一直线上依次有A，B，C，D 四点，且AB=CD，那么称AB 与CD 互为“对称线段”，其中 AB 为CD 的“对称线段”，CD 亦为AB 的“对称线段”.
如图2，下列情形中 AB 与CD 互为“对称线段”的是(填序号).
①AB=2，CD=3；②AB=1，BC=3，BD=5；③AC=7，BD=7.

(2)、【运用概念】如图3，AB 与CD 互为“对称线段”，点 M 为AC 的中点，点 N 为BD 的中点，且AB=2.直接写出 MN 的长为 .

(3)、【拓展提升】如图4，在同一直线上依次有A，B，C，D 四点，2AB=CD且AB=a(a 为常数)，点M 为AC 的中点，点 N 在BD 上且ND=mBD.是否存在m 的值使得MN 的长为定值?若存在，请求出 m 的值；若不存在，请说明理由.

查看解析
8、某粮库原有大米132 吨，一周内该粮库大米的进出情况如表：(运进大米记作“+”，运出大米记作“-”).
星期一
星期二
星期三
星期四
星期五
星期六
星期日
-32
+26
-23
-16
m
+42
-21

(1)、若经过这一周，该粮库存有大米88吨，求m 的值，并说明星期五该粮库是运进还是运出大米，运进或运出大米多少吨?

(2)、若大米进出库的装卸费用为每吨25元，求这一周该粮库需要支付的装卸总费用.

查看解析
9、甲、乙两商场上半年经营情况如下(“+”表示盈利，“一”表示亏本，以百万元为单位)
月份
一
二
三
四
五
六
甲商场
+0.8
+0.6
-0.4
-0.1
+0.1
+0.2
乙商场
+1.3
+1.5
-0.6
-0.1
+0.4
-0.1

(1)、三月份乙商场比甲商场多亏损多少元?

(2)、六月份甲商场比乙商场多盈利多少元?

(3)、甲、乙两商场上半年平均每月分别盈利或亏损多少元?

查看解析
10、我们把从1开始到n 的n个连续自然数的立方和记作 S_n ，那么有：
$S_{1} = 1^{3} = 1^{2} = {[\frac{1 \times (1 + 1)}{2}]}^{2} ， S_{2} = 1^{3} + 2^{3} = {(1 + 2)}^{2} = {[\frac{2 \times (1 + 2)}{2}]}^{2} ，$
$S_{3} = 1^{3} + 2^{3} + 3^{3} = {(1 + 2 + 3)}^{2} = {[\frac{3 \times (1 + 3)}{2}]}^{2} ， \dots$
观察上面式子的规律，完成下面各题：

(1)、猜想： $S_{n} =$ ；(用n 表示)；

(2)、依规律，直接写出 $1^{3} + 2^{3} + 3^{3} + \dots + 1 0^{3} = 3025 ；$

(3)、依规律，求 $1 1^{3} + 1 2^{3} + 1 3^{3} + \dots + 4 0^{3}$ 的值.

查看解析
11、

(1)、①观察一列数1，2，3，4，5，…，发现从第二项开始，每一项与前一项之差是1.根据此规律，如果 an(n为正整数)表示这个数列的第n项，那么a₁₈= ，a_n=；
②如果欲求1+2+3+4+…+n的值，可令S=1+2+3+4+…+n ①
将①式右边顺序倒置，得S=n+…+4+3+2+1 ②
由②加上①式，得 $2 S =$ ，∴ $S =$ ，
由结论求1+2+3+4+…+55=；

(2)、为了求 $1 + 3 + 3^{2} + 3^{3} + \dots + 3^{100}$ 的值，可令 $M = 1 + 3 + 3^{2} + 3^{3} + \dots + 3^{100} ，$ 则3M=3+ $3^{2} + 3^{3} + \dots + 3^{101} ，$ 因此 $3 M - M = 3^{101} - 1 ，$ 所以 $M = \frac{3^{101} - 1}{2} ，$ 即 $1 + 3 + 3^{2} + 3^{3} + \dots + 3^{100} =$ $\frac{3^{101} - 1}{2} .$ 仿照以上推理，计算： $1 + 5 + 5^{2} + 5^{3} + \dots + 5^{51} .$

查看解析
12、某物体由静止竖直向上运动，物体的高度h(单位：m)与运动时间t(单位：s)之间的关系可以用公式 $h = - 5 t^{2} + 150 t + 10$ 表示.

(1)、求运动时间分别为4s，10 s，20 s时该物体的高度；

(2)、估计运动时间为多少秒时，物体达到最高处?最大高度是多少?

查看解析
13、在1905年清朝学堂的课本中，用式子“ $\frac{五}{甲^{二}} ┬ \frac{三}{丙} ┴ \frac{四}{甲乙^{二}}$ ”来表示代数式” $\frac{a^{2}}{5} - \frac{c}{3} + \frac{a b^{2}}{4}$ ，则式子“ $\frac{三}{甲乙 ┬ 二甲^{三} 丙^{二} ┴ 六}$ ”表示的代数式为.

查看解析
14、单位体积的某种物质的质量叫作物质的密度.通常情况下，水的密度为 $1.0 \times 1 0^{3} k g / m^{3} ，$ 冰的密度为 $0.9 \times 1 0^{3} k g / m^{3} .$ 某制冰厂将a t水制成冰块后，求冰块的体积比水的体积大多少立方米?(用含a 的代数式表示)

查看解析
15、物理学家多贝尔发现蟋蟀的叫声频率和温度之间的计算公式： $T C = 10 + \frac{N - 40}{7} ，$ 这个公式也称为多贝尔定律，其中TC 表示摄氏温度，N表示蟋蟀每分钟鸣叫的次数.小勤统计后发现，蟋蟀平均每分钟鸣叫75次，则此时的温度为℃.

查看解析
16、如图，数轴上标出若干个点，每相邻的两点距离相等，其中点A，B，C，D对应的数分别是数a，b，c，d，a+b+c+d=2，a-b+c-d=-3.求a的值.

查看解析
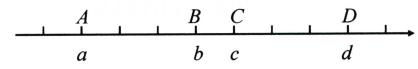
17、如图，数轴上标出若干个点，每相邻的两点相距1个单位长度，其中点A，B，C，D对应的数分别是整数a，b，c，d.若a+b+c+d=-2，那么数轴上与原点最接近的点是哪个点?

查看解析
18、如图，数轴上标出若干个点，每相邻的两点相距1个单位长度，其中点 A，B，C，D对应的数分别为整数a，b，c，d，且d-2a=4.那么数轴上的原点在哪一点上?

查看解析
19、

(1)、如图，在数轴上有若干个点，每相邻两个点之间的距离是1个单位长度，有理数a，b，c，d所表示的点是这些点中的四个，且在数轴上的位置如图所示.已知3a=4b-3，求c+2d的值；

(2)、如图，在数轴上标有若干个点，每相邻两点的间距相等，点A，B，C，D对应的数分别是a，b，c，d，且b+3c=10，b+3d=16，试求d-b 的值.

查看解析
20、计算：

(1)、 $(1 \frac{1}{2} + 1 \frac{1}{6} - 1 \frac{1}{12}) \div (- \frac{1}{12}) ；$

(2)、 $99 \times (- 99 \frac{98}{99}) .$

查看解析

上一页 754 755 756 757 758 下一页跳转

星期一	星期二	星期三	星期四	星期五	星期六	星期日
-32	+26	-23	-16	m	+42	-21

月份	一	二	三	四	五	六
甲商场	+0.8	+0.6	-0.4	-0.1	+0.1	+0.2
乙商场	+1.3	+1.5	-0.6	-0.1	+0.4	-0.1