-
1、
在抛物线形的喷泉水柱下设置一条安全的通道,可以让儿童在任意时间穿过安全通道时不被水柱喷到(穿梭过程中人的高度变化忽略不计).
素材1
图1为音乐喷泉,喷头的高度在垂直地面的方向上随着音乐变化而上下移动.不同高度的喷头喷出来的水呈抛物线型或抛物线的一部分,但形状相同,最大高度也相同,水落地点都在喷水管的右侧.

素材2
图2是当喷水头在地面上时(喷水头最低),其抛物线形水柱的示意图,水落地点离喷水口的距离为OM=4m,水柱最高点离地面3 m.图3 是某一时刻时,水柱形状的示意图. OA为喷水管,B为水的落地点,记OB 长度为喷泉跨度.

素材3
安全通道CD 在线段OB 上,若无论喷头高度如何变化,水柱都不会进入CD上方的矩形区域,则称这个矩形区域CDEF为安全区域.

问题解决:
(1)、在图2中,以O为原点,OM 所在直线为x轴,建立平面直角坐标系,求出抛物线的解析式;(2)、若喷水管OA 最高可伸长到2.25 m,求出喷泉跨度 OB 的最小值;(3)、现在需要一条宽为2m 的安全通道CD,为了确保进入安全通道CD上的任何人都能在安全区域内,则能够进入该安全通道的人的最大身高为多少?(精确到0.1m) -
2、如图,直线 与双曲线 交于B,C两点,点A 在第一象限内的双曲线上,且∠CAB=90°,求点A 的坐标.

-
3、如图,在△ABC中,∠BAC=90°,AB=2AC,点A(2,0),B(0,4),点C在第一象限内,双曲线 经过点C.将△ABC 沿y轴向上平移m 个单位长度,使点A 恰好落在双曲线上,求m 的值.

-
4、如图,矩形ABCD 的边AB 平行于x轴,反比例函数 的图象经过点B,D,对角线 CA 的延长线经过原点O,且AC=2AO.若矩形 ABCD 的面积是8,求 k的值.

-
5、如图,在平面直角坐标系中,▱OABC 的边OA 在 y 轴的正半轴上,反比例函数 0)的图象与▱OABC 分别交AB 于其中点D,交OC 于点E,且CE:OE=1:2,连接AE,DE,若S△ADE=2,则 k 的值为.

-
6、如图,函数 与 的图象分别是 C1 , C2 , 点 P 在C2上,PA∥y轴交C1 于点 A,PB∥x 轴交C1 于点B,则△PAB 的面积为.

-
7、如图,矩形 ABCD 的顶点A 和对称中心在反比例函数 的图象上,若矩形ABCD 的面积为8,则k 的值为.

-
8、 已知在△ABC 中,∠BAC=90°,AB=AC=6,D为BC的中点.
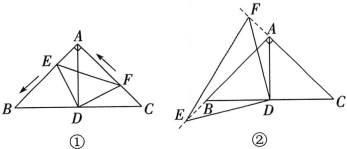 (1)、 如图①,若E,F 分别是AB, AC上的点,且 AE =CF,求证:△AED≌△CFD.(2)、 在(1)的条件下,求四边形 AEDF 的面积.(3)、若点 F,E 分别从点C,A 同时出发,以每秒1个单位的速度沿CA,AB 运动,到点A,B 时停止(如图①).设△DEF 的面积为y,点 F 运动的时间为 xs,求y 与x 之间的函数表达式.(4)、 在(3)的条件下,若点 F,E 分别沿CA,AB 的延长线继续运动(如图②),求此时y与x之间的函数表达式.
(1)、 如图①,若E,F 分别是AB, AC上的点,且 AE =CF,求证:△AED≌△CFD.(2)、 在(1)的条件下,求四边形 AEDF 的面积.(3)、若点 F,E 分别从点C,A 同时出发,以每秒1个单位的速度沿CA,AB 运动,到点A,B 时停止(如图①).设△DEF 的面积为y,点 F 运动的时间为 xs,求y 与x 之间的函数表达式.(4)、 在(3)的条件下,若点 F,E 分别沿CA,AB 的延长线继续运动(如图②),求此时y与x之间的函数表达式. -
9、 已知 与x2 成正比,y2 与x-2成正比,当x=1时,y=1;当x=-1时,y=-5.(1)、求y关于x的函数表达式.(2)、 当x=0时,求y的值.
-
10、在一矩形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是2:1.已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的宽是x米.(1)、求y与x之间的函数表达式.(2)、如果制作这面镜子共花了 195元,求这面镜子的长和宽.
-
11、观察下面的表格:
x
-1
0
1
ax2
1
12
7
若 则由表格中信息,得y与x 之间的函数表达式为;当x=3时,y的值为.
-
12、 若 是关于x的二次函数,则m=.
-
13、 如图,正方形 ABCD 的边长为5,F是BC 上一动点,过对角线的交点 E作EG⊥EF,交CD 于点G,连结 FG. 设 BF 的长为x,△EFG 的面积为y,则y与x之间的函数表达式为( )
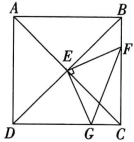 A、 B、 C、 D、
A、 B、 C、 D、 -
14、已知关于 x 的函数 (m-n)x(m+n≠0)的二次项系数与一次项系数的和为 , 差为2,则常数项为 ( )A、 B、 C、 D、
-
15、把下列二次函数化成一般形式,并分别指出二次项系数、一次项系数和常数项.(1)、 y=x(-2x+1)-x.(2)、
-
16、 如图,在 Rt△ABO 中,AB⊥OB,且 AB =OB=3,设直线x=t截此三角形所得的涂色部分的面积为S,则S 与t 之间的函数表达式为 (写出自变量的取值范围).

-
17、在半径为4cm的圆中,挖去一个半径为x cm的圆面,剩下的圆环的面积为 y cm2 , 则y 与x 之间的函数表达式为 , 其中自变量x 的取值范围是.
-
18、若 是二次函数,则a 的值是 ( )A、±2 B、– 2 C、2 D、无法确定
-
19、下列函数是二次函数的为( )A、y=3x B、y=-3x+5 C、 D、
-
20、如图,在平面直角坐标系中,抛物线 与x轴交于点A,B,与y轴交于点C,且直线y=x-6过点 B,与 y 轴交于点 D,点 C 与点 D 关于x轴对称,P是线段OB 上一动点,过点 P作x轴的垂线交抛物线于点M,交直线 BD于点N.
 (1)、求抛物线对应的函数表达式.(2)、 连结 MD,MB,当△MDB 的面积最大时,求点 P 的坐标.(3)、在(2)的条件下,在y 轴上是否存在点Q,使得以 Q,M,N为顶点的三角形是直角三角形?若存在,求出点 Q 的坐标;若不存在,请说明理由.
(1)、求抛物线对应的函数表达式.(2)、 连结 MD,MB,当△MDB 的面积最大时,求点 P 的坐标.(3)、在(2)的条件下,在y 轴上是否存在点Q,使得以 Q,M,N为顶点的三角形是直角三角形?若存在,求出点 Q 的坐标;若不存在,请说明理由.