-
1、一天,李明和爸爸一起到建筑工地去,看见了一个如图所示的人字架,爸爸说:“李明,我考考你! 这个人字架中的∠3=110°,你能求出∠1比∠2大多少吗?”请你帮李明计算一下.

-
2、 如图所示,在△ABC中,∠ACB=90°,将△ACD沿CD折叠,使点A恰好落在BC边上的点E处.若∠B=26°,则∠BDE=.

-
3、 把命题“在同一平面内,垂直于同一直线的两条直线平行”改写成“如果……那么……”的形式为.
-
4、 如图,在△ABC中,点D,E分别在BC,AC上,且AB∥DE,∠1=∠2.求证:AF∥BC.

-
5、 请判断命题“若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形”的真假性.若是真命题,请说明理由;若是假命题,请举反例说明.
-
6、 把7支铅笔放到3个抽屉里,总有一个抽屉里至少放3支. .(填“正确”或“错误”)
-
7、 将命题“绝对值相等的两个数互为相反数”改写成“如果……那么……”的形式为.
-
8、 在△ABC中,有一边长是另一边长的2倍,已知有两条边长分别是3cm,8cm,则△ABC的周长为cm.

-
9、 下列命题是假命题的是( )A、若a>0,b>0,则a+b>0 B、直角都相等 C、若|a|=6,则a=6 D、两直线平行,同位角相等
-
10、 一个三角形三个内角的度数之比为2:5:7,则这个三角形一定是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形
-
11、 如图,在△ABC中,D,E分别为BC,AB上的点,则以D为顶点的三角形的个数有( )
 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个 -
12、 如图,已知. 的两条高AD,CE相交于点F,且.
 (1)、求证:(2)、若 求CF的长.
(1)、求证:(2)、若 求CF的长. -
13、 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为CE的中点,连结AD,此时∠CAD=24°,∠ACB=66°.求证:BE=AC.

-
14、 如图,点F,D在△ABC的边BC上,点E,G分别在AB,AC上.请从三个选项:①∠1+∠2=180°;②∠DGC=∠BAC;③EF∥AD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.

-
15、 如图所示,在△ABC中,D是AB上一点,CF∥AB,DF交AC于点E,DE=EF.
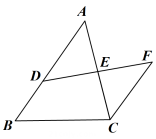 (1)、求证:△ADE≌△CFE;(2)、若AB=5,CF=3,求BD的长.
(1)、求证:△ADE≌△CFE;(2)、若AB=5,CF=3,求BD的长. -
16、 如图,所有小正方形的边长都为1个单位,点A,B,C均在格点上.按下述要求画图,并回答问题:
 (1)、画射线AC;(2)、过点C画线段AB的平行线CD;(3)、过点A画线段BC的垂线,垂足为E.
(1)、画射线AC;(2)、过点C画线段AB的平行线CD;(3)、过点A画线段BC的垂线,垂足为E. -
17、 如图,在△ABC中,AD是△ABC的角平分线,点F在射线AD上,FE⊥BC于点E,∠C=80°,∠B=36°,则∠F=°.

-
18、 如图,在△ABC中,∠ACB的平分线交AB于点D,DE⊥AC于点E,F为BC上一点,若DF= 则△AED的面积为( )
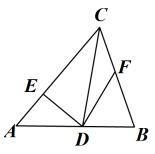 A、2 B、2.5 C、3 D、5
A、2 B、2.5 C、3 D、5 -
19、 如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形.图中△ABC是格点三角形,请你找出方格中所有与△ABC全等,且以A为顶点的格点三角形,这样的三角形(△ABC除外)的个数有( )
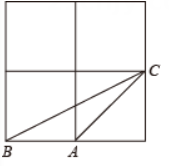 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
20、 如图,已知∠BAD=∠CAE,AD=AB,下列添加的条件中不能证明△ABC≌△ADE的是( )
 A、∠B=∠D B、BC=DE C、∠C=∠E D、AC=AE
A、∠B=∠D B、BC=DE C、∠C=∠E D、AC=AE