-
1、如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.若AB=4,AD=x,△DEF的面积为y,则y关于x的函数图象大致为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
2、在△ABC中,∠C=90°,tanA , AC=2 , 则BC的长为( )A、1 B、2 C、 D、5
-
3、在平面直角坐标系xOy中,将点A(3,1)绕原点O逆时针旋转90°,得到点B,则点B的坐标为( )A、(3,﹣1) B、(﹣1,3) C、(1,﹣3) D、(﹣3,1)
-
4、如图是一个几何体的三视图(图中尺寸单位:cm),则这个几何体的底面圆的周长为( )
 A、6πcm B、9πcm C、12πcm D、16πcm
A、6πcm B、9πcm C、12πcm D、16πcm -
5、已知直线y=kx+b经过第一、第二、第三象限,则k,b的取值范围是( )A、k<0,b<0 B、k<0,b>0 C、k>0,b<0 D、k>0,b>0
-
6、上午9时整,钟表的时针和分针构成的角的度数为( )A、30° B、60° C、90° D、120°
-
7、如图,将△ABC沿着射线BC平移到△DEF.若BC=6,EC=4,则平移的距离为( )
 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8 -
8、《2025年中国卫星导航与位置服务产业发展白皮书》显示,去年我国卫星导航与位置服务产业总产值达5758亿元.将“5758亿”用科学记数法表示为( )A、5.758×1010 B、5.758×1011 C、0.5758×1012 D、57.58×1010
-
9、计算(﹣2)×(﹣3),正确的结果是( )A、﹣5 B、5 C、﹣6 D、6
-
10、已知点 , , 在函数的图象上,则的大小关系是( )A、 B、 C、 D、
-
11、已知 , 互为相反数, , 互为倒数,则的值为 .
-
12、(1)补全数轴;
(2)把表示右边各数的点画在数轴上; , , ,
(3)用“”把这些数连接起来.

-
13、在平面直角坐标系中,抛物线 与x轴交于点A(-3,0),B(1,0),与 y轴交于点C,顶点为 D,连结AD.
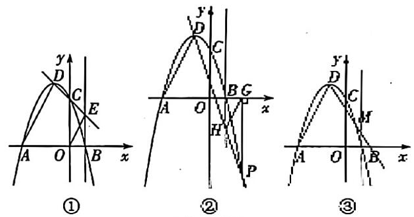 (1)、 ① 如图①,直线CD 交直线.x=1于点E,连结OE.求证:
(1)、 ① 如图①,直线CD 交直线.x=1于点E,连结OE.求证:②如图②,P(2,-5)为抛物线 上一点,过点 P 作. 轴,垂足为G.直线DP 交直线x=1于点 H,连结HG.求证:
(2)、通过上述两种特殊情况的证明,你是否有所发现?请仿照(1)写出你的猜想,并证明,且在图③上画出草图.在平面直角坐标系中,抛物线 与x轴交于点A(-3,0),B(1,0),顶点为 D,M为该抛物线上一动点(不与点A,B,D重合). -
14、已知M 为抛物线 的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
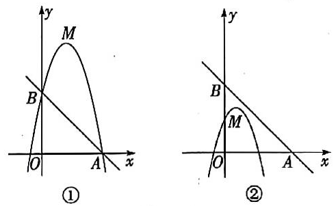 (1)、判断点 M 是否在直线.y=4x+1上,并说明理由.(2)、如图①,若抛物线也经过点A,B,当 时,根据图象,求出x的取值范围.(3)、 如图②,点A 的坐标为(5,0),点 M 在 内部,若点 都在抛物线上,试比较y1与y2的大小.
(1)、判断点 M 是否在直线.y=4x+1上,并说明理由.(2)、如图①,若抛物线也经过点A,B,当 时,根据图象,求出x的取值范围.(3)、 如图②,点A 的坐标为(5,0),点 M 在 内部,若点 都在抛物线上,试比较y1与y2的大小. -
15、一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索. 与缆索 均呈抛物线形,桥塔AO 与桥塔BC 均垂直于桥面.如图,以O为原点,直线FF'为x轴,桥塔AO所在直线为y轴,建立平面直角坐标系.缆索. 所在抛物线与缆索 所在抛物线关于y 轴对称,桥塔AO与桥塔BC 之间的距离(OC=100m,AO=BC=17m,缆索 的最低点 P 到FF'的距离PD=2m(桥塔的粗细忽略不计).
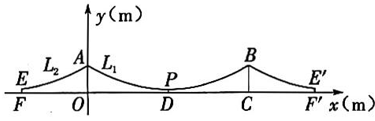 (1)、求缆索. 所在抛物线对应的函数表达式.(2)、点 E 在缆索. 上, 且EF=2.6m,FO<OD,求 FO的长.
(1)、求缆索. 所在抛物线对应的函数表达式.(2)、点 E 在缆索. 上, 且EF=2.6m,FO<OD,求 FO的长. -
16、2024年“五一”假期期间,阆中古城景区某特产店销售A,B两类特产. A类特产的进价为50元/件,B类特产的进价为60元/件.已知购买1件A 类特产和1件B 类特产需132元,购买3件A 类特产和5件B 类特产需540元.(1)、求A 类特产和B 类特产的售价.(2)、A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每件每降价1元,每天可多售出10件(售价不低于进价).设每件A 类特产降价x元,每天的销售量为y件,求y 与x之间的函数表达式,并写出自变量x 的取值范围.(3)、在(2)的条件下,由于 B 类特产供货紧张,每天只能购进100 件且能按原价售完.设该特产店每天销售这两类特产的总利润为ω元,求ω与x之间的函数表达式,并求出当每件A 类特产降价多少元时,总利润最大,最大总利润是多少元.
-
17、已知函数 (b,c为常数)的图象经过点((0,-3),(-6,-3).(1)、 求b,c 的值.(2)、 当 时,求y 的最大值.(3)、当 时,若y的最大值与最小值之和为2,求m 的值.
-
18、在平面直角坐标系中,已知抛物线C 经过点(0,3)和(1,1).(1)、求抛物线C 对应的函数表达式.(2)、将抛物线C先向左平移2个单位,再向下平移1个单位,得到抛物线( , 求抛物线 的顶点坐标.
-
19、如图,二次函数 的图象经过点 P(-2,3).
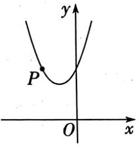 (1)、求a 的值和图象的顶点坐标.(2)、已知点 Q(m,n)在该二次函数的图象上.
(1)、求a 的值和图象的顶点坐标.(2)、已知点 Q(m,n)在该二次函数的图象上.①当m=2时,求n的值.
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
-
20、抛物线 经过点(1,-2),(-2,13).(1)、 求a,b 的值.(2)、若 是抛物线上不同的两点,且 求m 的值.