-
1、如图,在中, , 点、、分别是边、、的中点,则下列结论错误的是( )
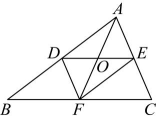 A、 B、 C、 D、
A、 B、 C、 D、 -
2、某几何体的三视图如图所示,这个几何体是( )
 A、圆柱 B、圆锥 C、正方体 D、长方体
A、圆柱 B、圆锥 C、正方体 D、长方体 -
3、宿迁市年第一季度总量突破一千亿大关,约为亿元.数据亿用科学记数法表示为( )A、 B、 C、 D、
-
4、下列计算结果为的是( )A、 B、 C、 D、
-
5、在平面直角坐标系xOy中,反比例函数的图象经过点A(1,5),点A,B关于原点对称.该函数图象上另有两点M1 , M2 , 它们的横坐标分别为m,m+n,其中m>1,n>0.依次作直线AM1 , BM1与y轴分别交于点C1 , D1 , 直线AM2 , BM2与y轴分别交于点C2 , D2.记OC1﹣OD1=d1 , OC2﹣OD2=d2 .(1)、若m=2,求OC1的长;(2)、求代数式(m+n)•d2的值;(3)、当m(d1﹣d2)=2d2 , 3(d1+d2)=2n3时,求点D2关于直线AM2对称的点P的坐标.
-
6、如图,矩形ABCD中,对角线AC,BD相交于点O.M是BC的中点,DM交AC于点G.
 (1)、求证:AG=2GC;(2)、设∠BCD,∠BDC的角平分线交于点I.
(1)、求证:AG=2GC;(2)、设∠BCD,∠BDC的角平分线交于点I.①当AB=6,BC=8时,求点I到BC的距离;
②若AB+AC=2BC,作直线GI分别交BD,CD于E,F两点,求的值.
-
7、综合与实践:学校数学兴趣小组围绕“校园花圃方案设计”开展主题学习活动.
已知花圃一边靠墙(墙的长度不限),其余部分用总长为60m的栅栏围成.兴趣小组设计了以下两种方案:
方案一
方案二
如图1,围成一个面积为450m2的矩形花圃.

如图2,围成矩形花圃时,用栅栏(栅栏宽度忽略不计)将该花圃分隔为两个小矩形区域,用来种植不同花卉,并在花圃两侧各留一个宽为3m的进出口(此处不用栅栏).
 (1)、求方案一中与墙垂直的边的长度;(2)、要使方案二中花圃的面积最大,与墙平行的边的长度为多少米?
(1)、求方案一中与墙垂直的边的长度;(2)、要使方案二中花圃的面积最大,与墙平行的边的长度为多少米? -
8、如图,PA与⊙O相切于点A,AC为⊙O的直径,点B在⊙O上,连接PB,PC,且PA=PB.
 (1)、连接OB,求证:OB⊥PB;(2)、若∠APB=60°,PA=2 , 求图中阴影部分的面积.
(1)、连接OB,求证:OB⊥PB;(2)、若∠APB=60°,PA=2 , 求图中阴影部分的面积. -
9、为继承和弘扬中华优秀传统文化,某校将八年级学生随机安排到以下四个场所参加社会实践活动.

已知小明、小华、小丽都是该校八年级学生,求下列事件的概率:
(1)、小明到南通博物苑参加社会实践活动;(2)、小华和小丽都到南通美术馆参加社会实践活动. -
10、为提升学生体质健康水平,促进学生全面发展,某校大课间共开展6项体育活动,每名学生均参加了其中一项活动.为了解该校学生参与大课间体育活动情况,随机抽取了该校50名学生进行调查,得到如下未完成的统计表.
体育活动
足球
篮球
排球
乒乓球
跳绳
啦啦操
人数
6
a
10
9
8
5
 (1)、表格中a的值为 ;(2)、若该校有1000名学生,请估计该校参加足球活动的学生人数;(3)、为备战校际篮球联赛,学校计划从参加篮球活动的甲、乙两名同学中选拔一人加入校篮球队.已知甲、乙两名同学近六周定点投篮测试成绩(每次测试共有10次投篮机会,以命中次数作为测试成绩)如图所示.你建议选拔哪名同学,请说明理由.
(1)、表格中a的值为 ;(2)、若该校有1000名学生,请估计该校参加足球活动的学生人数;(3)、为备战校际篮球联赛,学校计划从参加篮球活动的甲、乙两名同学中选拔一人加入校篮球队.已知甲、乙两名同学近六周定点投篮测试成绩(每次测试共有10次投篮机会,以命中次数作为测试成绩)如图所示.你建议选拔哪名同学,请说明理由. -
11、请从下列四个命题中选取两个命题,并判断所选命题是真命题还是假命题.如果是真命题,给出证明;如果是假命题,举出反例.
⑴若a2=b2 , 则a=b;
⑵对于任意实数x,y,一定有x2+y2>2xy;
⑶两个连续正奇数的平方差一定是8的倍数;
⑷一组对边平行,另一组对边相等的四边形一定是平行四边形.
-
12、(1)、解不等式组;(2)、计算 .
-
13、如图,网格图中每个小正方形的面积都为1.经过网格点A的一条直线,把网格图分成了两个部分,其中△BMN的面积为3,则sin∠MNB的值为 .

-
14、在平面直角坐标系中,以点A(3,0)为圆心,为半径作⊙A.直线y=kx﹣3k+2与⊙A交于B,C两点,则BC的最小值为 .
-
15、我国南宋数学家秦九韶曾提出利用三角形的三边求面积的公式:一个三角形的三边长分别为a,b,c,三角形的面积S.若a=2 , b=3,c=1,则S的值为 .
-
16、如图,一块砖的A,B,C三个面的面积比是5:3:1.如果B面向下放在地上,地面所受压强为a Pa,那么C面向下放在地上时,地面所受压强为 Pa.

-
17、把一根长10m的钢管截成3m长和1m长两种规格的钢管.为了不造成浪费,可能截得钢管的总根数为 (写出一种情况即可).
-
18、南通是“建筑之乡”,工程建筑中经常采用三角形的结构.如图是屋架设计图的一部分,E是斜梁AC的中点,立柱AD,EF垂直于横梁BC.若AC=4.8m,∠C=30°,则EF的长为 m.

-
19、分解因式am+a= .
-
20、在平面直角坐标系xOy中,五个点的坐标分别为A(﹣1,5),B(1,2),C(2,1),D(3,﹣1),E(5,5).若抛物线y=a(x﹣2)2+k(a>0)经过上述五个点中的三个点,则满足题意的a的值不可能为( )A、 B、 C、 D、