-
1、有一水果摊,其侧面示意图如图所示,AB,CD分别是水果摊前挡板,后挡板,AB,CD均与水平地面BC 垂直,AB=50cm,CD=140cm,坡面 AD 是水果放置区,坡比为1:2,在后挡板CD的正上方点E 处安装顶棚EF,DE=60cm,且 , 此时顶棚的另一端点 F 到前挡板AB 的水平距离GB=60cm.

求:
(1)、水果放置区的水平宽度 BC.(2)、顶棚端点 F 离地面的高度 FG(结果精确到1cm,参考数据: -
2、如图,公路旁有两个高度相同的路灯AB,CD,小明上午上学时发现路灯AB 在太阳光下的影子恰好落到里程碑E 处,他自己的影子恰好落在路灯 CD 的底部C处.晚自习放学时,小明站在上午同一个地方,发现在路灯CD 的灯光下自己的影子恰好落在里程碑E 处.
 (1)、在图中画出小明的位置(用线段 FG 表示),并画出光线,标出太阳光、灯光.(2)、若上午上学时,高1米的木棒在太阳光下的影长为2米,小明的身高为1.5米,他离里程碑 E 的距离恰好为5米,求路灯的高度.
(1)、在图中画出小明的位置(用线段 FG 表示),并画出光线,标出太阳光、灯光.(2)、若上午上学时,高1米的木棒在太阳光下的影长为2米,小明的身高为1.5米,他离里程碑 E 的距离恰好为5米,求路灯的高度. -
3、如图, 内接于⊙O,AB 是⊙O的直径,点 F 在⊙O上,且满足 过点C作⊙O的切线交AB 的延长线于点D,交AF 的延长线于点E.
 (1)、 求证:(2)、若 求AF 的长.
(1)、 求证:(2)、若 求AF 的长. -
4、辘轳(如图①)是从杠杆演变来的汲水工具,据《物原》记载:“史佚始作辘轳”.这说明早在公元前一千一百多年前我国已经发明了辘轳.如图②所示为从辘轳抽象出来的几何模型,在 中, , O是边AC上一点,以OA 长为半径的⊙O与AB 相交于点P,CP=CB.
 (1)、 求证:直线CP 是⊙O 的切线.(2)、 若 , 求⊙O 的半径.
(1)、 求证:直线CP 是⊙O 的切线.(2)、 若 , 求⊙O 的半径. -
5、如图,已画出了几何体的三视图的一部分.
 (1)、添补俯视图中缺的部分.(2)、标注左视图中“?”处的数据.(3)、求这个几何体的表面积.
(1)、添补俯视图中缺的部分.(2)、标注左视图中“?”处的数据.(3)、求这个几何体的表面积. -
6、如图,在 中,AD 是边BC 上的高,E 为边AC的中点, 求:
 (1)、 线段CD 的长.(2)、的值.
(1)、 线段CD 的长.(2)、的值. -
7、已知α是锐角,且 求 的值.
-
8、如图,AB 是半圆O的直径,半径( , D 是OC 的延长线上一点,DE 切半圆O于点E,连结AE,交OC 于点F.若( , 则EF 的长为.
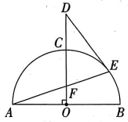
-
9、如图,小明在距离地面30米的点 P 处测得斜坡点A 处的俯角为 , 测得斜坡点 B 处的俯角为 .若斜坡AB 的坡比为 , 则斜坡 AB 的长是米.
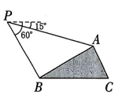
-
10、如图,在一个半径为4厘米,高为4厘米的圆柱的中间依次向下挖去半径分别为3厘米、2厘米、1厘米,高分别为2厘米、1厘米、0.5厘米的圆柱,则最后得到的立体图形的表面积是平方厘米(结果保留π).
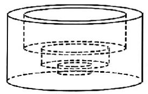
-
11、如图所示的图案是用一把直尺、含60°角的三角尺和光盘摆放而成的,A为直角三角尺的斜边与直尺的交点,B为光盘与直尺的唯一交点.若AB=3,则光盘的直径是.

-
12、 如图,在菱形ABCD 中, 则tan∠DBE 的值为.

-
13、由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小正方体的个数,则x+y=.
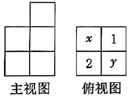
-
14、 如图,⊙O 内切于Rt△ABC,点 P,Q分别在直角边BC、斜边AB 上,PQ____AB,且PQ与⊙O 相切.若AC=2PQ,则 tanB 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、如图,太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上投影的长是 , 则皮球的直径是( )
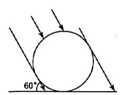 A、 B、15cm C、10cm D、
A、 B、15cm C、10cm D、 -
16、一艘货轮从小岛A 正南方向的点B 处向西航行30km到达点C 处,然后沿北偏西60°方向航行20km到达点 D 处,此时观测到小岛A 在北偏东60°方向,则小岛A 与出发点B 之间的距离为( )
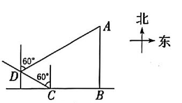 A、 B、 C、 D、
A、 B、 C、 D、 -
17、 如图,在四边形ABCD 中, , O为AB 的中点,以点O为圆心,AO长为半径作圆,恰好使得点 D 在⊙O 上,连结OD,若 则下列说法中,错误的是( )
 A、D 是 的中点 B、CD 是⊙O 的切线 C、AE∥OD D、
A、D 是 的中点 B、CD 是⊙O 的切线 C、AE∥OD D、 -
18、如图,以正六边形ABCDEF 的顶点A 为圆心,AB 长为半径作⊙A,与正六边形ABCDEF 重合的扇形部分恰好是一个圆锥的侧面展开图,则该圆锥的底面半径与母线长之比为( )
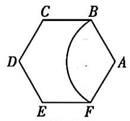 A、 B、 C、 D、12
A、 B、 C、 D、12 -
19、 如图,AB 是⊙O的直径,C,D 是⊙O上的点,∠CDB=15°,过点C作⊙O 的切线交AB 的延长线于点E,则 sin E 的值为( )
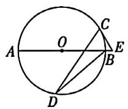 A、12 B、 C、 D、
A、12 B、 C、 D、 -
20、 如图, M是边OA 上一点,以点M 为圆心,3cm为半径作⊙M.当OM=5cm时,⊙M 与直线OB 的位置关系是( )
 A、相离 B、相交 C、相切 D、无法确定
A、相离 B、相交 C、相切 D、无法确定