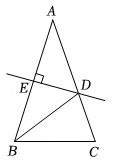
-
1、如图，在△ABC中，∠ACB＝45°，CD平分∠ACB，BE⊥AC于点E，CD⊥AB于点D，且与BE交于点H，EF⊥BC于点F，且与CD交于点G．则下面的结论：①BF＝FC；②EG＝EH；③BH＝HE；④DB＝DG．其中正确结论的序号有 ．
-
2、如图，矩形纸片ABCD中，AB＝4cm，BC＝8cm，现将纸片折叠压平，使A与C重合，折痕为EF，则AE的长为 ．
-
3、若关于x、y的二元一次方程组的解满足x+y≤0，则m的取值范围是 ．
-
4、如图，两根竹竿AB和BD斜靠在墙CE上，量得∠CAB，∠CDB的度数分别为51°，34°，则这两根竹竿的夹角∠ABD的度数是 °．
-
5、如图，已知∠DBC＝∠ACB，要证明：△ABC≌△DCB．
⑴若以“SAS”为依据，则需要添加的一个条件是 ．
⑵若以“AAS”为依据，则需要添加的一个条件是 ．
-
6、如图，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PG∥AD交BC于点F，交AB于点G，连结CP，有下列结论：①∠ACB＝2∠APB；②S△PAC：S△PAB＝PC：PB；③BP垂直平分CE；④∠PCF＝∠CFP，其中一定正确的是（ ）
A、①② B、①③ C、②③ D、③④ -
7、如图所示，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，则∠2的度数为（ ）
A、45° B、50° C、55° D、60° -
8、若 ， 则（ ）A、x＜﹣2y B、2x＜y C、2x+y＞0 D、x+2y＞0
-
9、如图，在△ABC中，AB＝AC＝8，DE垂直平分AB，△BDC周长为13，则BC的长为（ ）
A、4 B、5 C、6 D、7 -
10、下列能断定△ABC为等腰三角形的是（ ）A、∠A＝40°，∠B＝70° B、∠A＝20°，∠B＝70° C、AB＝AC＝3，BC＝7 D、AB＝1，BC＝4，周长为6
-
11、不等式x+3＜0的解集表示在数轴上正确的是（ ）A、
B、
C、
D、
-
12、下列图形是轴对称图形的是（ ）A、
B、
C、
D、
-
13、粮库三天内发生粮食进出库的吨数如下： ， ， ， ， ， （其中“”表示进库，“”表示出库）(1)、经过这三天，仓库管理员结算发现库里还存粮吨，那么三天前库里存粮多少吨？(2)、如果进出的装卸费都是每吨元，那么这三天要付多少装卸费？
-
14、有理数 ， ， 在数轴上对应点的位置如图所示：化简 ．
-
15、拿起圆规和直尺，耐心做一做，不写作法，保留作图痕迹．
已知线段、 ， 作线段（要求：保留作图痕迹）．
-
16、计算：(1)、；(2)、 ．
-
17、如图，在数轴上，点B在点A的右侧．已知点A 对应的数为 ， 点B对应的数为m， 点C到原点的距离为2，且 ， 则m的值为 ．
-
18、已知 ， 则 ．
-
19、计算： （结果用度表示）
-
20、如图，射线在的内部，图中共有个角： ， 和 ， 若其中一个角的度数是另一个角度数的两倍，则称射线是的“平衡线”若 ， 且射线是的“平衡线”，则的度数为（ ）
A、 B、或 C、或 D、或或