-
1、中国已经成为全球最大并且最有活力的新能源汽车市场.中国汽车工业协会数据显示,某品牌新能源汽车2022年5月份销量为10万辆,7月份销量为14.5万辆.设该品牌新能源汽车的月平均增长率为 , 则( )A、 B、 C、 D、
-
2、将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )
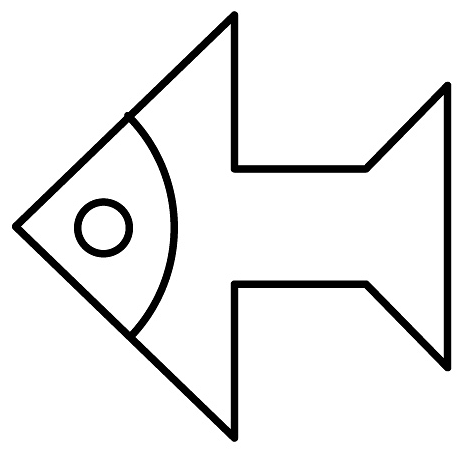 A、
A、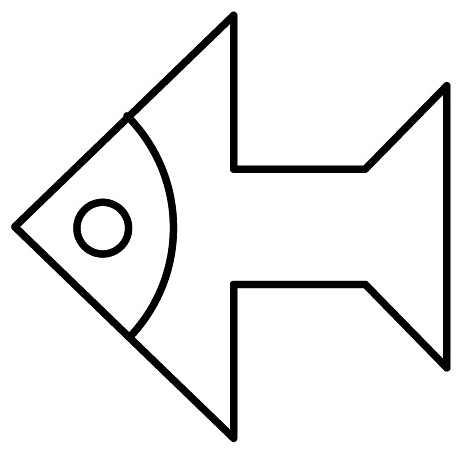 B、
B、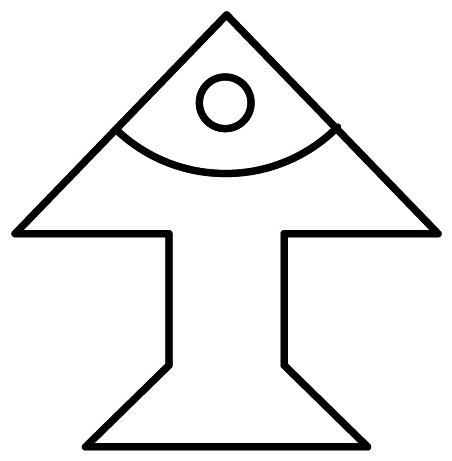 C、
C、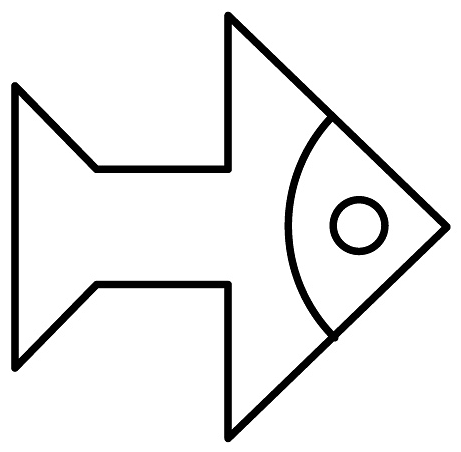 D、
D、
-
3、方程的解是( )A、 B、 C、 D、没有实数根
-
4、2024年4月,中国航天成功发射神舟十八号飞船.下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、
 中国探火
B、
中国探火
B、 中国火箭
C、
中国火箭
C、 中国探月
D、
中国探月
D、 中国行星探测
中国行星探测
-
5、综合实践
【活动交流】数学活动课上,周老师让学生用一段绳子(无弹性)沿着三角板的两直角边边缘拉直滑动.
如图1,第一次拉成折线 , 且 , 第二次拉成折线 , 探究绳子两个端点之间距离的变化情况.
周老师和同学们在探究时,有如下交流:
小明:两种不同位置,绳子的两个端点的距离不一样,即 .
小聪:我发现问题可抽象为:如图 , 在中, , 在和延长线上分别取点 , , 若 , 则 .
小颖:小聪,在探究你的问题的过程中,我发现点是中点.
周老师:小聪发现的结论是正确的,当绳子两端到角顶点距离相等时,绳子两端距离最小.
结合上述师生的交流完成下面任务:
【探究论证】
(1)如图2,请你证明小颖发现的结论;
(2)如图2,请你证明小聪发现的结论;
【创新应用】
(3)如图3,中, , , , 点 , , 分别在边 , , 上,若 , 求的最小值.

-
6、(1)观察下列命题完成填空:
①若 , 则有或 ,
②若 , 则有或 ,
③若 , 则有或 ,
④若 , 则有或 ,
…
按规律猜想:若(括号内为 ),则有或______;
(2)若把(1)中命题改为:“若 , 则有或”仍然成立,猜想m,n,k应满足的等量关系式为______,并证明该命题成立;
(3)对于(2)中的m,n,k , 若满足 , 求的值.
-
7、对于任意非负整数 , , 若满足: , 则称为与的“2次幂差数”.(1)、下列两个数:① , ② , 其中不是“2次幂差数”的是______(填序号);(2)、若为与的“2次幂差数”,且 , 是两个连续的正整数,证明:为奇数;(3)、若为与的“2次幂差数”,且 , , 求的最小值.
-
8、如图,在的正方形网格中,的三个顶点都在格点上,请使用无刻度直尺按要求作图.(注意先用铅笔画,再用水笔描,求作的图形用实线,辅助的线条用虚线)
 (1)、在图1中,画出边上的高;(2)、在图2中,画出边上的中线;(3)、在图3中,画 , 使与全等(F不与C重合,画出一个即可).
(1)、在图1中,画出边上的高;(2)、在图2中,画出边上的中线;(3)、在图3中,画 , 使与全等(F不与C重合,画出一个即可). -
9、为进一步发展新质生产力,某企业计划对现有甲、乙两类生产线的设备进行更新换代,经测算,升级1条甲类生产线比升级条乙类生产线需多投入万元,用万元升级甲类生产线的条数和用万元升级乙类生产线的条数相同,设升级条乙类生产线需投入万元.(1)、升级条甲类生产线需投入______万元,用万元升级甲类生产线的条数为______条;(用含的式子表示)(2)、升级一条甲类、乙类生产线各需投入多少资金?
-
10、如图,点A,D,B,E在一条直线上, , , , 求证: .

-
11、先化简,再求值: , 其中 .
-
12、化简:(1)、;(2)、 .
-
13、如图,中, , , E为垂足,点D在上,且 , 若 , , 则的长为 .

-
14、如图,两个正方形放置于长方形内(正方形的两边在长方形的边上),长方形是两正方形的重叠部分,已知阴影部分①与阴影部分②的周长之差为m,面积之差为n,则(用含m、n的代数式表示).

-
15、如图,中, , , 过点 , 点分别作 , 的垂线相交于点 , 则 .

-
16、若分式的值为零,则 .
-
17、如图,正方形是由四个全等的直角三角形和小正方形拼成,连接 , , 若想求出图中阴影部分的面积,只需知道( )
 A、的长 B、的长 C、的长 D、的长
A、的长 B、的长 C、的长 D、的长 -
18、若实数 , , 满足 , , 则的值为( )A、0 B、1 C、2 D、3
-
19、如图,中, , , 为边上的高,E,F为 , 上的点, , 若 , 则的面积为( )
 A、4 B、8 C、12 D、16
A、4 B、8 C、12 D、16 -
20、点与点关于( )对称A、x轴 B、y轴 C、原点 D、直线x=5