-
1、某校希望进一步提高学生体育与健康素养,为了解学生每天校外体育活动时间,随机抽取了若干名学生进行调查,将这些学生一天的校外体育活动时间x(分钟)分为五个小组:
A:0≤x<15 B:15≤x<30 C:30≤x<45 D:45≤x<60 E:60≤x<75
现将调查结果绘制成两幅不完整的统计图。
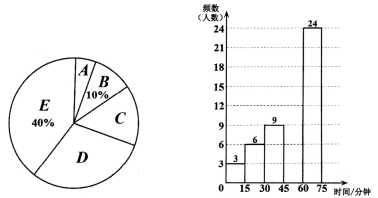
请根据统计图信息,解答下列问题:
(1)、本次调查的样本容量是 ▲ , 并将频数分布直方图补充完整;(2)、若该校共有学生3000人,请根据调查结果估计,该校学生每天校外体育活动时间不少于60分钟的学生有多少人?(3)、已知A组有1名男生和2名女生,从中随机抽取2名学生,请用列表法或画树状图的方法,求恰好抽到1名男生和1名女生的概率. -
2、如图,AB=DC , AC=DB . 求证:△ABC≌△DCB .
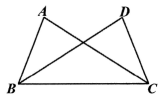
-
3、解不等式组: , 并把解集在数轴上表示出来.

-
4、解分式方程:= .
-
5、计算:22-4sin30°+(π+1)0- .
-
6、如图,在菱形ABCD中,∠ABC=60°,AB=4,连接BD , 点P是BD上的一个动点,连接PA , PC , 则PA+PB+PC的最小值是 .
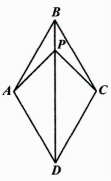
-
7、如图,在平面直角坐标系中,直线AB交x轴于点A(1,0),交y轴于点B(0,2),以原点O为圆心,适当长为半径画弧,交x轴于点C , 交y轴于点D , 分别以点C , D为圆心,大于CD的长为半径画弧,两弧在第一象限内交于点E , 作射线OE交AB于点F , 则点F的坐标是 .
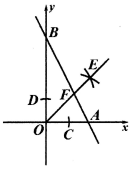
-
8、如图,点D , E分别是△ABC边AB , AC上的点,且DE∥BC , 若= , 则的值是 .

-
9、关于x的一元二次方程x2-x+2m=0有两个相等的实数根,则m= .
-
10、一家鞋店在一段时间内销售了某款女鞋50双,各种尺码的销售量如表1所示:
表1
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
2
4
7
19
10
6
2
根据上述信息,在鞋的尺码组成的数据中,众数是 .
-
11、如图,在正方形ABCD中,AB=6,点E是BC的中点,把△ABE沿AE折叠,点B落在点F处,延长EF交CD于点G , 连接AG , 则AG的长为( )
 A、3 B、2 C、2 D、4
A、3 B、2 C、2 D、4 -
12、观察下列一组数:
1.9,3.99,5.999,7.9999,9.99999,…
按此规律,第n个数是( )
A、2n-0.1n B、2n+1-0.1n C、2n-1+0.9n D、2n-1-0.1n -
13、一个三角形花坛的面积是6m2 , 它的一边a(单位:m)是这边上的高h(单位:m)的函数,此函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
14、如图,在⊙O中,直径AB=6,BC是⊙O的弦,若∠B=60°,则的长为( )
 A、6π B、4π C、2π D、π
A、6π B、4π C、2π D、π -
15、若代数式有意义,则实数x的取值范围是( )A、x>2 B、x≥2 C、x<2 D、x≤2
-
16、如图,△ABC为等腰三角形,AB=AC , 点D是BC延长线上的一点,∠ACD=110°,则∠A的度数为( )
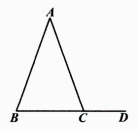 A、70° B、55° C、40° D、35°
A、70° B、55° C、40° D、35° -
17、下列运算正确的是( )A、x+x=x2 B、(x3)2=x5 C、2x2⋅5x2=10x2 D、(xy)2=x2y2
-
18、截至2024年,西藏自治区图书馆的藏书量已超过500000册.数据500000用科学记数法表示为( )A、0.5×106 B、5×105 C、5×104 D、50×104
-
19、下列美术字中,可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
20、18的绝对值是( )A、18 B、-18 C、 D、-