-
1、如图是由小正方形组成的的网格,小正方形的顶点称为格点, , , , , 五个点均为格点,是线段与网格线的交点,仅用无刻度的直尺在给定网格中完成画图,每个画图任务的画线不得超过三条.
 (1)、在图(1)中,若点和关于点中心对称,画点;(2)、在图(1)中,若点绕点逆时针旋转后得到点 , 画点;(3)、在图(2)中,在线段上画点 , 使;(4)、在图(2)中,画满足条件的格点 , 使 .
(1)、在图(1)中,若点和关于点中心对称,画点;(2)、在图(1)中,若点绕点逆时针旋转后得到点 , 画点;(3)、在图(2)中,在线段上画点 , 使;(4)、在图(2)中,画满足条件的格点 , 使 . -
2、如图,已知直线交于两点,为的直径,为上一点,平分 , 过点作于点 .
 (1)、求证:为的切线;(2)、若已知的半径为5,且 , 求的长.
(1)、求证:为的切线;(2)、若已知的半径为5,且 , 求的长. -
3、二次函数中的的部分取值如下表:根据表中数据填空:
x
…
0
1
2
3
…
y
…
m
n
0
…
(1)、该函数图象的对称轴是______;(2)、该函数图象与轴的交点的坐标是______;(3)、当时,的取值范围是______;(4)、不等式的解集是______. -
4、如图,在中, , , , 点从点开始沿边运动,速度为 . 与此同时,点从点开始沿边运动,速度为 . 当点到达点时,点同时停止运动.连接 , 设运动时间为 , 的面积为 .
 (1)、用含的代数式表示:______cm,______cm;(2)、当为何值时?
(1)、用含的代数式表示:______cm,______cm;(2)、当为何值时? -
5、解方程:
-
6、如图,已知 , 均为等腰直角三角形, , 为的中点,的延长线交线段于点 , 连接 . 若 , , 则 .

-
7、已知抛物线(为常数,)经过点 , , 且 , 则下列四个结论:①;②;③若方程有两个不相等的实数根(且),则;④若 , 抛物线过点 , 且 , 则 . 其中正确的结论是(填序号).
-
8、若关于的方程的两个实数根互为相反数,则的值是 .
-
9、某航空公司有若干个飞机场,每两个飞机场之间都开辟了一条航线,一共开辟了条航线,这个航空公司共有个飞机场.
-
10、在平面直角坐标系中,将函数的图象记为 , 将绕原点旋转得到图象 , 把和合起来的图形记为图形 . 则当时,直线与图形的交点的个数是( )A、2 B、4 C、2或3 D、3或4
-
11、如图,四边形内接于 , , , 的直径为 , 四边形的周长为 , 的长为 , 则关于的函数关系式是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、已知抛物线上有三个点 , , , 若 , , , 则 , , 的大小关系是( )A、 B、 C、 D、
-
13、在平面直角坐标系中,点坐标 , 以为圆心,4个单位长度为半径作圆,下列正确的是( )A、原点在内 B、原点在上 C、与轴相切,与轴相交 D、与轴相切,与轴相交
-
14、如图,将绕点逆时针旋转,点的对应点为 , 点的对应点为 , 若恰好是线段与的交点,且 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、如图,内接于 , 连 , 若 , 则的度数是( )
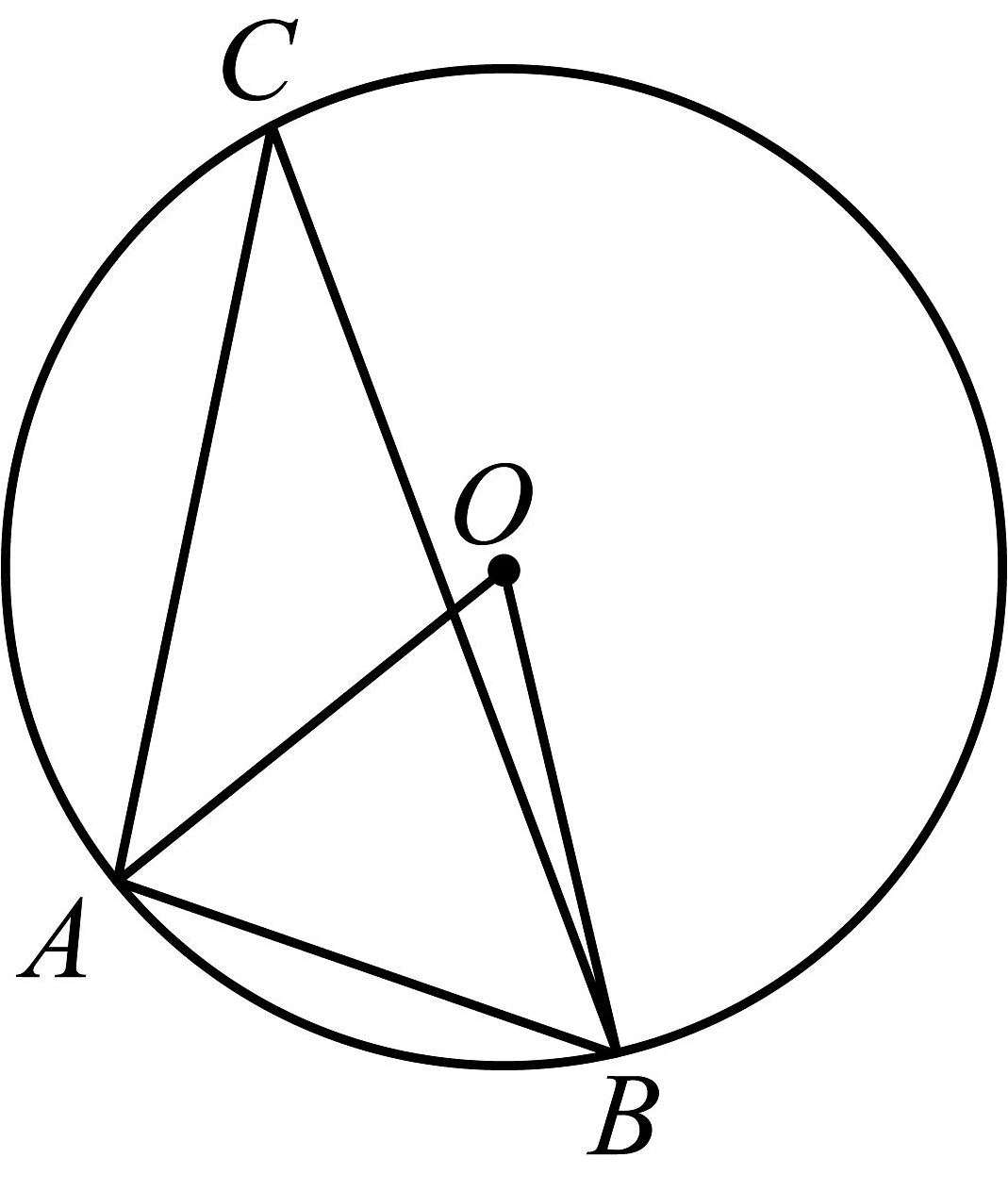 A、 B、 C、 D、
A、 B、 C、 D、 -
16、关于抛物线 , 下列说法正确的是( )A、开口向上 B、对称轴是直线 C、函数有最小值 D、可由抛物线向右平移个单位再向下平移个单位而得
-
17、下列图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、在一元二次方程中,二次项系数、一次项系数、常数项分别是( )A、2,1, B、2, , 1 C、2,1,1 D、2, ,
-
19、如图,中, , , 在的顶点 , 处各有一只小蚂蚁,它们同时出发,分别以相同速度由点向点和由点向点爬行,经过后,它们分别爬行到了点 , 点处,连接 , 交于点 .
 (1)、求证:;(2)、小蚂蚁在爬行过程中,的大小会变化吗?若变化,请说明理由;若不变,求的度数.
(1)、求证:;(2)、小蚂蚁在爬行过程中,的大小会变化吗?若变化,请说明理由;若不变,求的度数. -
20、甲地和乙地都种植相同品种的水稻,甲地的种植面积为亩,乙地的种植面积为亩 , 最后两块土地收获的水稻重量都是请问甲地每亩水稻的产量是乙地的多少倍?你能根据计算结果直接写出哪一块土地每亩水稻产量更高吗?