相关试卷

1、如果 $\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = 2$ ，那么 $\frac{x - y + z}{a - b + c} =$ ．

查看解析
2、菱形的对角线长分别为6和8，则该菱形的面积是（）

A、24 B、48 C、12 D、10

查看解析
3、下列方程是一元二次方程的是（　　）

A、 $2 x + 1 = 0$ B、 $x^{2} - 3 x + 1 = 0$ C、 $a x^{2} + x = 1$ D、 $\frac{1}{x^{2}} - 1 = 2$

查看解析
4、如图， $∠ A = ∠ B$ ， $A E = B E$ ，点 $D$ 在 $A C$ 边上， $∠ 1 = ∠ 2$ ， $A E$ 和 $B D$ 相交于点 $O$ ．求证： $△ A E C ≌ △ B E D$ ．

查看解析
5、如图，数轴上线段 $A B = 3$ （单位长度），线段 $C D = 6$ （单位长度），点 $A$ 在数轴上表示的数是 $- 12$ ，点 $C$ 在数轴上表示的数是16．若线段 $A B$ 以每秒3个单位长度的速度向右匀速运动，同时线段 $C D$ 以每秒2个单位长度的速度向左匀速运动．设运动时间为 $t s$ ．

(1)、点 $B$ 在数轴上表示的数为　　，点 $D$ 在数轴上表示的数为　　，

(2)、当点 $B$ 与点 $C$ 相遇时，求点 $A$ ， $D$ 在数轴上表示的数；

(3)、当运动到 $B C = 8$ （单位长度）时，求出此时点 $B$ 在数轴上表示的数．

查看解析
6、某文具店最近购进了一批钢笔，进价为每支6元，售价为每支12元．每天的销售数量以20支为标准，每天售出超出20支的部分记为正，不足20支的部分记为负．该文具店记录了5天该钢笔的销售情况，如下表所示．
第1天
第2天
第3天
第4天
第5天
每天售出的数量（支）
$- 2$
$+ 4$
0
$- 5$
$+ 7$

(1)、在这5天中，第一天售出该种钢笔支，销售数量最多的一天比销售数量最少的一天多售出钢笔支；

(2)、求该文具店这5天出售这种钢笔的总利润；

(3)、该文具店为了促销这种钢笔，决定推出下列两种促销方案：
方案一：若购买数量不超过5支，每支12元；若超过5支，则超过部分每支降价4元；
方案二：每支均打七五折销售．
在促销期间，王老师在该文具店购买10支该种钢笔作为奖品，通过计算说明应选择上述两种促销方案中的哪种方式购买更省钱．

查看解析
7、阅读第①小题计算方法，再类比计算第②小题．
（1）① $- 5 \frac{5}{6} + (- 9 \frac{2}{3}) + 17 \frac{1}{2} + (- 3 \frac{1}{2})$
解：原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{1}{2}) + [(- 3) + (- \frac{1}{2})]$
$= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{1}{2} + (- \frac{1}{2})]$
$= 0 + (- 1 \frac{1}{2})$
$= - 1 \frac{1}{2}$ ．
上面这种方法叫做拆项法．
②计算： $(- 2022 \frac{5}{6}) + (- 2022 \frac{2}{3}) + (- 1 \frac{1}{2}) + 4045$ ．
（2）① $1 - \frac{1}{2^{2}} = \frac{1}{2} \times \frac{3}{2}$ ， $1 - \frac{1}{3^{2}} = \frac{2}{3} \times \frac{4}{3}$ ， $1 - \frac{1}{4^{2}} = \frac{3}{4} \times \frac{5}{4}$ ， …，上面这种方法叫做裂项法．
②计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times \cdot \cdot \cdot \times (1 - \frac{1}{2021^{2}}) \times (1 - \frac{1}{2022^{2}})$ ．

查看解析
8、某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位： $km$ ）
第1批
第2批
第3批
第4批
第5批
$5 km$
$- 2 km$
$- 4 km$
$- 3 km$
$10 km$

(1)、接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

(3)、第几次行驶后出租车离公司最远？

查看解析
9、如图，在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛．若圆形的半径为 $r$ 米，广场的长为 $a$ 米，宽为 $b$ 米．

(1)、列式表示广场空地的面积；

(2)、若 $a = 50$ ， $b = 20$ ， $r = 2$ ，求广场空地的面积（ $m$ 取3）．

查看解析
10、打一篇稿子，每分打字个数与所需的时间如下表：
每分打字个数 $a$ （个）
$120$
$100$
$75$
$60$
所需时间 $t$ （分钟）
$25$
$30$
$40$
$50$

(1)、每分打字个数 $a$ 和所需时间 $t$ 成　　比例关系，可以表示为　　．

(2)、如果每分打 $150$ 个字，打完这篇稿子需要多少分钟？

查看解析
11、先化简，再求值： $10 y^{2} + 3 (x - 2 y^{2}) - (3 y^{2} + 7 x)$ ，其中 $x = - \frac{1}{4}$ ， $y = 5$ ．

查看解析
12、计算： $- 1^{4} + [2 - {(- 3)}^{2}] + | - 8 | \div 4$ ．

查看解析
13、在数轴上表示0， $- (- 3)$ ， $|- 5|$ ， $- 3 \frac{1}{2}$ ， $- 2$ 并按从小到大的顺序用“ $<$ ”连接起来．

查看解析
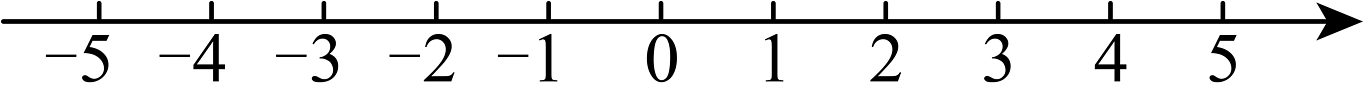
14、计算： $(- 12) \times (\frac{1}{4} + \frac{1}{6} - \frac{1}{2})$ ．

查看解析
15、我们常用的数是十进制的数，而计算机程序处理中使用的是只有数码0和1的二进制数．这两者可以相互换算，如将二进制数101换算成十进制数应为 $1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0} = 4 + 0 + 1 = 5$ ，将1101换算成十进制数应为 $1 \times 2^{3} + 1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0} = 13$ ，按此方式，则将十进制数25换算成二进制数应为．

查看解析
16、气温由 $- 5 ° C$ 上升了 $4 ° C$ 后的气温是 $° C$ ．

查看解析
17、观察下列一组图形中点的个数，其中第①个图形中共有4个点，第②个图形中共有12个点，第③个图形中共有24个点，按此规律，第⑧个图形有（）个点．

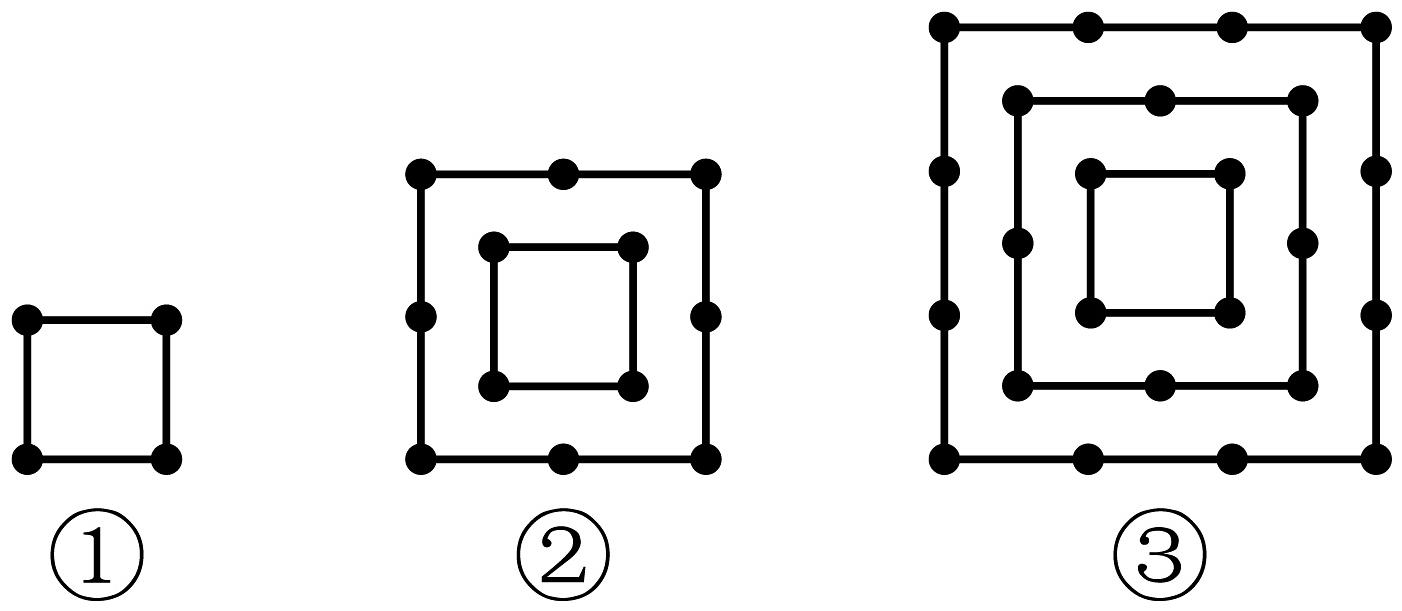A、96 B、112 C、144 D、160

查看解析
18、已知 $| a + 5 | + {(b - 2)}^{2} = 0$ ，则 $a^{b}$ 的值为（）

A、25 B、 $- 25$ C、10 D、 $- 10$

查看解析
19、某数学兴趣小组在暑假开展社会实践活动，销售某品牌书包，平均每天可以销售20个，每个盈利12元，为了扩大销售，增加盈利，该小组决定采取适当的降价措施，经调查发现，如果每个书包每降价1元，平均每天可以多卖5个．

(1)、若该兴趣小组同学想要一天盈利300元，每个书包应降价多少元；

(2)、该兴趣小组同学想要一天盈利最大，应降价多少元，所得最大利润是多少元？

查看解析
20、在平面直角坐标系中，抛物线 $y = x^{2}$ 的图象如图所示．已知 $A$ 点坐标为 $(1, 1)$ ，过点 $A$ 作 $A A_{1} ∕ ∕ x$ 轴交抛物线于点 $A_{1}$ ，过点 $A_{1}$ 作 $A_{1} A_{2} ∕ ∕ O A$ 交抛物线于点 $A_{2}$ ，过点 $A_{2}$ 作 $A_{2} A_{3} ∕ ∕ x$ 轴交抛物线于点 $A_{3}$ ，过点 $A_{3}$ 作 $A_{3} A_{4} ∕ ∕ O A$ 交抛物线于点 $A_{4}$ ……，依次进行下去，则点 $A_{2019}$ 的坐标为．

查看解析

上一页 798 799 800 801 802 下一页跳转

	第1天	第2天	第3天	第4天	第5天
每天售出的数量（支）	$- 2$	$+ 4$	0	$- 5$	$+ 7$

第1批	第2批	第3批	第4批	第5批
$5 km$	$- 2 km$	$- 4 km$	$- 3 km$	$10 km$

每分打字个数 $a$ （个）	$120$	$100$	$75$	$60$
所需时间 $t$ （分钟）	$25$	$30$	$40$	$50$