-
1、如图,面积为4的等边三角形中,D,E,F分别是的中点,则的面积是( )
 A、1 B、 C、 D、
A、1 B、 C、 D、 -
2、若某三角形的三边长分别为2,4,m,则m的值可以是( )A、1 B、5 C、7 D、10
-
3、如图所示的方格纸中,每个小正方形的边长均为1,点A,B,C在小正方形的顶点上.
 (1)、画出中边上的高;(2)、画出中边上的中线;(3)、的面积为 .
(1)、画出中边上的高;(2)、画出中边上的中线;(3)、的面积为 . -
4、如图,在中, , D为延长线上一点,点E在边上,且 , .
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
5、如图,树垂直于地面,为测树高,小明在处,测得 , 他沿方向走到处,线段米,测得 , 求树的高度.

-
6、如图,已知点B、F、C、E在一条直线上, , , . 求证: .

-
7、如图,已知 , , , 求证: .

-
8、a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).

-
9、在平面直角坐标系中,的顶点坐标 , , .
 (1)、在图中作出关于y轴对称的图形;(2)、在y轴上找一点P,使最短,在图中标出P点的位置并写出P点坐标.
(1)、在图中作出关于y轴对称的图形;(2)、在y轴上找一点P,使最短,在图中标出P点的位置并写出P点坐标. -
10、如图,在 , 中, , , , 点 , , 三点在同一条直线上,连接 , . 以下四个结论:①;②;③;④ , 其中正确的结论是(填序号).

-
11、如图,已知 , 平分 , , 在上,在上,在上.当取最小值时,此时的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图,在平分角的仪器中, , , 将点A放在一个角的顶点,和分别与这个角的两边重合,能说明就是这个角的平分线的数学依据是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图, , .
 (1)、求的度数;(2)、若 , 求证: .
(1)、求的度数;(2)、若 , 求证: . -
14、 如图,在和中, , , . 连接 , 点是的中点,连接 .
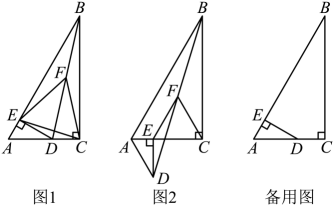 (1)、如图1,当点在上时,求证:是等边三角形;(2)、将图1中的△ADD绕点A顺时针旋转.
(1)、如图1,当点在上时,求证:是等边三角形;(2)、将图1中的△ADD绕点A顺时针旋转.①当旋转角为60°时,如图2所示,(1)中的结论还成立吗?说明理由;
②当EF最长时,EF与AD的交点记作M.若AE=3,则EM= ▲ .
-
15、 如图,抛物线与轴负半轴交于点 , 与轴交于点 , 顶点的横坐标为 .
 (1)、求抛物线的表达式;(2)、如图1,将直线沿轴向上平移个单位长度,当它与抛物线有交点时,求的取值范围;(3)、如图2,抛物线的对称轴交直线于点 , 交轴于点 , 连接 . 抛物线上是否存在点(不与点重合),使得 . 若存在,直接写出点的横坐标;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、如图1,将直线沿轴向上平移个单位长度,当它与抛物线有交点时,求的取值范围;(3)、如图2,抛物线的对称轴交直线于点 , 交轴于点 , 连接 . 抛物线上是否存在点(不与点重合),使得 . 若存在,直接写出点的横坐标;若不存在,说明理由. -
16、 如图,四边形内接于⊙平分 , 连接 .
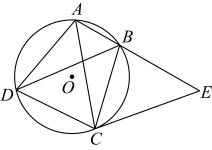 (1)、求证:;(2)、延长至点 , 使 , 连接 . 求证: .
(1)、求证:;(2)、延长至点 , 使 , 连接 . 求证: . -
17、 宁夏葡萄酒品质优良,深受消费者青睐.为了解某基地的葡萄种植情况,九(1)班同学对该基地的试验田中甲、乙两种葡萄树的产量进行调查.(1)、【调查与收集】
甲、乙两种葡萄树各种植了500株,计划从中各抽取100株作为各自的样本.以下抽样调查方式合理的是____.
A、依次抽取100株 B、随机抽取100株 C、在长势较好的葡萄树中随机抽取100株 D、在方便采摘的葡萄树中随机抽取100株(2)、【整理与描述】同学们采用合理的抽样调查方式获得甲、乙两个样本中每株的产量(单位:kg),将所得数据整理描述如下:
甲样本的频数分布表
频数
7
45
15
20
13
乙样本的频数分布直方图

注:每组含最小值,不含最大值.
根据以上信息,解答问题:
①甲样本中组的频率是 ▲ ;
②补全乙样本的频数分布直方图.
(3)、【分析与应用】①填表:
样本
平均数(kg)
中位数出现的组别
方差
甲
5.73
乙
15.74
4.85
(计算平均数时,把各组中每株的产量用这组数据的中间值代替,如的中间值为)
②估计试验田中甲种葡萄树每株产量不低于的株数;
③结合以上数据为基地的葡萄种植提出一条合理化建议.
-
18、 如图,在的方格中,每个小正方形边长均为1个单位长度.的顶点、点和点都在格点上.仅用无刻度直尺作图,保留作图痕迹,不写作法.
 (1)、过点作的垂线段;(2)、过点作的平行线.
(1)、过点作的垂线段;(2)、过点作的平行线. -
19、 中国结起源于旧石器时代的结绳记事,唐宋时期发展为装饰艺术,明清达到鼎盛.某种中国结有大、小两个型号,编织一个大号需用绳4米,编织一个小号需用绳3米.
 (1)、编织这种中国结恰用绳25米,则大、小号各编织多少个?(2)、计划用不超过1200米的绳子编织350个这种中国结,一个大号的利润为12元,一个小号的利润为8元.当大号编织多少个时总利润最大?最大利润是多少?
(1)、编织这种中国结恰用绳25米,则大、小号各编织多少个?(2)、计划用不超过1200米的绳子编织350个这种中国结,一个大号的利润为12元,一个小号的利润为8元.当大号编织多少个时总利润最大?最大利润是多少? -
20、 定义:若一个三位数的十位数字减去个位数字的差恰好等于百位数字,则这个三位数叫做“极差数”.例如,三位数 , 因为 , 所以它是“极差数”.(1)、【理解定义】
三位数是否为“极差数”? .
(2)、【建模推理】设一个“极差数”的百位、十位、个位数字分别为 , 则与的关系式为;
(3)、任意一个“极差数”都能被11整除吗?为什么?