相关试卷

1、如图，点A，B，C在⊙O上，∠BAC=50°，则∠OBC的度数为.

查看解析
2、如图，正五边形ABCDE内接于⊙O，P为AB上一点，连接PA，PE，则∠APE的度数为（）

A、18° B、36° C、54° D、72°

查看解析
3、如图，四边形ABCD内接于⊙O， $\hat{A B} = \hat{B C}$ ，连接BD，若∠ABC=70°，则∠BDC的度数为（）

A、20° B、35° C、55° D、70°

查看解析
4、如图，CD是⊙O的直径，点A，B在⊙O上.若AC=BC，∠AOC=36°，则∠D=（）

A、9° B、18° C、36° D、45°

查看解析
5、如图，点A，B，C在⊙O上，∠AOB=100°，∠C的度数是（）

A、40° B、50° C、80° D、100°

查看解析
6、已知二次函数 $y = x^{2} + 2 a x - 3 a .$

(1)、若函数图象经过点(2，5)，
①求该二次函数的表达式；
②若将平面内一点 A(m，n)向左平移5个单位或向右平移4个单位，都恰好落在函数y= $x^{2} + 2 a x - 3 a$ 的图象上，求m 的值.

(2)、设 $M (x_{1}, y_{1}) ， N (x_{2}, y_{2})$ 是该函数图象上不同的两点，且 $x_{1} + x_{2} = 3 ，$ 求证： $y_{1} +$ $y_{2} > \frac{9}{2} .$

查看解析
7、已知二次函数 $y = a {(x - 1)}^{2} - a - 3 (a⟩ 0) .$

(1)、若二次函数的图象经过(2，-5)，(1，-4)，(-1，-6)三点中的某一个点.
①判断该二次函数的图象经过上述三点中的哪一个点；
②当x≥m时，该函数的最小值是-3，求m的值.

(2)、若二次函数的图象经过点(n，p)，(n+3，q)，求当p<q时，n 的取值范围.

查看解析
8、已知二次函数 $y = - x^{2} + b x +$ c(b，c 为常数).

(1)、若该二次函数的图象经过点(3，0)，(0，-3).
①求该二次函数的表达式；
②将该二次函数的图象向左平移m(m>0)个单位，得到新的二次函数的图象.若新二次函数的图象的顶点恰好落在直线 y=-2x-3上，求 m 的值.

(2)、若二次函数 $y = - x^{2} + b x + c$ 的图象上有且仅有一个点的纵坐标是横坐标的2倍，且当1≤x≤2时，该二次函数的最大值是2，求b的值.

查看解析
9、已知二次函数 $y = - x^{2} + b x + c$ 的图象经过(-1，0)与(5，0)两点.若关于x 的方程 $- x^{2} + b x + c + d = 0$ 有两个根，其中一个根是6，则该方程的另一个根是.

查看解析
10、在二次函数 $y = a x^{2} + b x - 2$ 中，x与 y 的几组对应值如下表：
x
··
—2
0
1

y

-2
-2
1

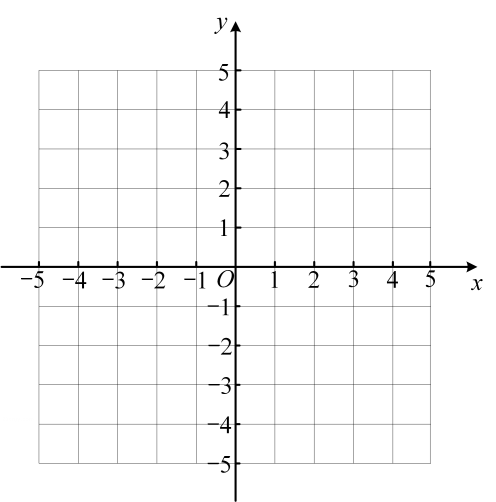(1)、求二次函数的表达式；

(2)、求二次函数图象的顶点坐标，并在给出的平面直角坐标系中画出二次函数的图象；

(3)、将二次函数的图象向右平移n个单位后，当0≤x≤3时，若图象对应的函数最大值与最小值的差为5，请直接写出n 的值.

查看解析
11、如图，在平面直角坐标系xOy中，二次函数 $y = a x^{2} - 4 x + 5 (a \neq 0)$ 的图象的顶点为 A，此图象与x轴交于点 B和点C，与y轴交于点 D.点A 的横坐标是-2.

(1)、求 B，C 两点的坐标；

(2)、平移该二次函数的图象，使点 A 恰好落在点D 的位置上，求平移后图象对应的二次函数的表达式.

查看解析
12、若将抛物线 $y = 2 x^{2} - 4 x + 5$ 向下平移m(m>0)个单位，向左平移n(n>0)个单位后得到的抛物线的表达式为y=2x² ，则m+n=

查看解析
13、如图，二次函数 $y = a x^{2} + b x + c (a ， b ，$ c 为常数，a≠0)的图象交x 轴于A，B 两点，点 A 的坐标是(-1，0)，点 B 的坐标是(n，0).有下列结论：①abc<0；②4a+c>2b；③关于x 的方程 $a x^{2} +$ bx+c=0的解是x₁=-1，x₂=n； $④ - \frac{b}{2 a} =$ $\frac{n - 1}{2} .$
其中正确的有( )

A、1个 B、2个 C、3个 D、4个

查看解析
14、关于 x 的二次函数 $y = m x^{2} - 2 m x + m + 1$ (m<-1)的图象可能是( )

A、 B、 C、 D、

查看解析
15、已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则 ( )

A、abc<0 B、2a+b<0 C、2b-c<0 D、a-b+c<0

查看解析
16、已知二次函数 $y = - x^{2} + 2 a x - a + 3$ (a是常数).

(1)、若该函数图象的对称轴为直线x=1，求该函数的表达式；

(2)、当x≥a+1时，该函数的最大值为4，求a的值；

(3)、已知M(x₁ ， y₁)和 N(3a，y₂)是该函数图象上两点，当 $2 \leq x_{1} \leq 3$ 时，y₁

查看解析
17、已知二次函数 $y = a x^{2} - 4 a x + 3$ 的图象上有A(a，y₁)，B(4，y₂)两点，则下列说法正确的是( )

A、当0<a<2时， $y_{1} > y_{2}$ B、当a>2时， $y_{1} < y_{2}$ C、当a<0时， $y_{1} < y_{2}$ D、当a>4时， $y_{1} < y_{2}$

查看解析
18、已知二次函数y=x(x-a)+(x-a)(x-b)+x(x-b)，其中a，b为两个不相等的实数.

(1)、当a=0，b=3时，求此函数图象的对称轴.

(2)、当b=2a 时，若该函数在0≤x≤1时，y随x的增大而减小；在3≤x≤4时，y随x 的增大而增大，求a 的取值范围.

(3)、若点A(a，y₁)，B(a+b/₂ ， y₂)，C(b，y₃)均在该函数的图象上，是否存在常数m，使得 $y_{1} + m y_{2} + y_{3} = 0 ?$ 若存在，求出m 的值；若不存在，说明理由.

查看解析
19、已知抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 的顶点坐标为(-2，-1)，下列说法正确的是( )

A、 $a = \frac{1}{2}$ B、当x=-2时，二次函数有最小值为3 C、当x>-2时，y随x 的增大而减小 D、当-3<x<-1时，y<0

查看解析
20、已知一个二次函数的图象开口向下，顶点的坐标为(2，1)，那么这个二次函数的表达式可以是 .(只需写出一个即可)

查看解析

上一页 240 241 242 243 244 下一页跳转

x	··	—2	0	1
y		-2	-2	1