版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、设命题 $p$ ：关于 $x$ 的方程 $x^{2} + m x + 1 = 0$ 有两个不相等的实数根， $q$ ：关于 $x$ 的方程 $4 x^{2} + (4 m - 2) x + 1 = 0$ 无实数根．

(1)、若 $p$ 为真，求实数 $m$ 的取值范围；

(2)、若 $p$ 、 $q$ 有且仅有一个为真命题，求实数m的取值范围．

查看解析
2、已知函数 $f (x) = \sqrt{x + 5} + \frac{1}{x - 7}$
（1）求函数的定义域；
（2）求 $f (11)$ ， $f (\frac{5}{4})$ 的值；
（3）当 $a > 0$ 时，求 $f (a)$ ， $f (a - 1)$ 的值．

查看解析
3、已知 $x > 1$ ，函数 $y = x + \frac{1}{x - 1}$ 的最小值是（）

A、3 B、4 C、5 D、6

查看解析
4、如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，E为棱 $D D_{1}$ 的中点， $P$ 为底面正方形 $A B C D$ 内（含边界）的动点，则（）

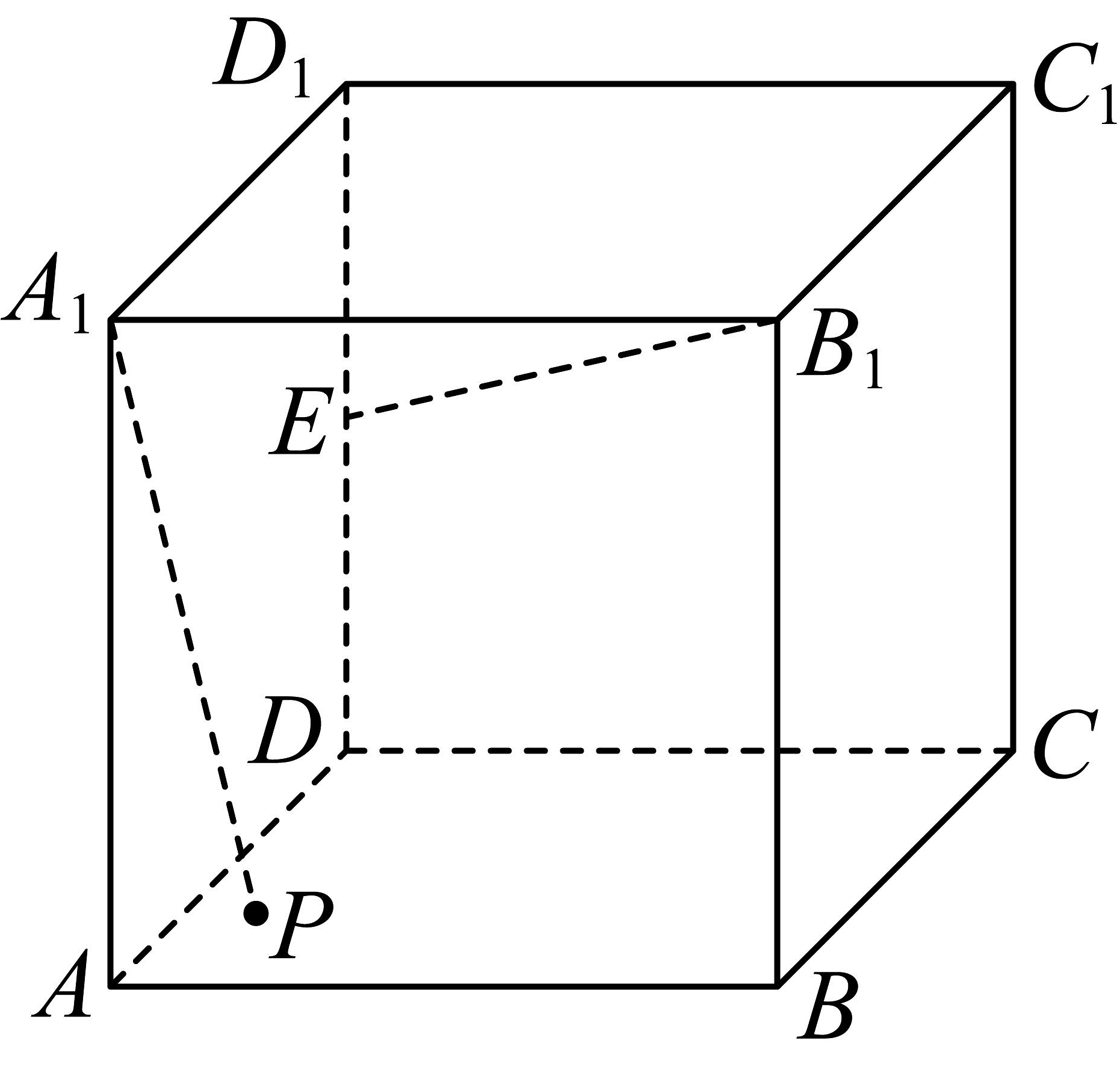A、三棱锥 $B_{1} - A_{1} D_{1} P$ 的体积为定值 B、直线 $B_{1} E / /$ 平面 $A_{1} B D$ C、当 $A_{1} P ⊥ B D$ 时，点 $E$ 到平面 $A_{1} A P$ 的距离为 $\frac{\sqrt{2}}{2}$ D、当 $∠ A P A_{1}$ 的正切值为2时，动点P的轨迹长度为 $\frac{π}{4}$

查看解析
5、已知 $3 < x < 7, 1 < y < 2$ ，则 $\frac{y}{x}$ 的取值范围是.

查看解析
6、已知实数 $x, y > 0$ ，且 $\frac{2}{x} + \frac{1}{y} = 1$ ，若 $2 x + y > m^{2} - 8 m$ 恒成立，则实数 $m$ 的取值范围为（）

A、 $(- 9, 1)$ B、 $(- 1, 9)$ C、 $[- 1, 9]$ D、 $(- \infty, - 1) \cup (9, + \infty)$

查看解析
7、已知 $O$ 为坐标原点，动点 $P$ 到 $x$ 轴的距离为 $d$ ，且 $| O P |^{2} = λ + μ d^{2}$ ，其中 $λ, μ$ 均为常数，动点 $P$ 的轨迹称为 $(λ, μ)$ 曲线.

(1)、若 $(\frac{1}{2}, μ)$ 曲线为焦点在 $y$ 轴上的椭圆，求 $μ$ 的取值范围.

(2)、设曲线 $Ω$ 为 $(9, - \frac{1}{8})$ 曲线，斜率为 $k (k \neq 0)$ 的直线 $l$ 过 $Ω$ 的右焦点，且与 $Ω$ 交于 $A, B$ 两个不同的点.
（i）若 $k = 2$ ，求 $|A B|$ ；
（ii）若点 $B$ 关于 $x$ 轴的对称点为点 $D$ ，证明：直线 $A D$ 过定点.

查看解析
8、一个袋子中有4个红球，6个绿球，采用不放回方式从中依次随机取出2个球．事件A＝“两次取到的球颜色相同”；事件B＝“第二次取到红球”；事件C＝“第一次取到红球”．下列说法正确的是（）

A、 $A \subseteq B$ B、事件B与事件C是互斥事件 C、 $P (A B) = \frac{2}{15}$ D、 $P (B + C) = \frac{2}{3}$

查看解析
9、已知 $F_{1}, F_{2}$ 分别为椭圆 $C : \frac{x^{2}}{9} + \frac{y^{2}}{b^{2}} = 1 (b > 0)$ 的左､右焦点， $P (2, \frac{5}{3})$ 为 $C$ 上一点，则 $C$ 的离心率为， $△ P F_{1} F_{2}$ 内切圆的半径为.

查看解析
10、已知函数 $f (x) = a e^{x} - x$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $a > 0, \forall x \in (0, + \infty), f (x) > \frac{e^{- x}}{a} - \frac{1}{x}$ ，求 $a$ 的取值范围.

查看解析
11、已知全集 $U = A \cup B = \{0, 1, 2, 3, 4, 5\}, A \cap (∁_{U} B) = \{1, 3, 5\}$ ，则集合 $B =$ （）

A、 $\{1, 3, 5\}$ B、 $\{0, 2, 4\}$ C、 $\emptyset$ D、 $\{0, 1, 2, 3, 4, 5\}$

查看解析
12、已知集合 $A = \{x ∣ x^{2} - 9 x + 18 \leq 0\}$ ， $B = {x ∣ 4 < x < 9}$ .

(1)、分别求 $A \cap B$ ， $A \cup B$ .

(2)、已知 $C = {x ∣ m - 2 < x < m + 1}$ ，且 $C \subseteq B$ ，求实数 $m$ 的取值范围.

查看解析
13、已知 $a > 0$ ， $b > 0$ ．

(1)、比较 $a^{2} + a$ 与 $2 a b - b^{2}$ 的大小；

(2)、若 $a + 9 b + 7 = a b$ ，求 $a b$ 的最小值；

(3)、若 $b + \frac{1}{a} = a (a \leq 5)$ ，求 $b$ 的取值范围．

查看解析
14、已知集合 $A = \{x |x^{2} + 6 x < 55\}$ ， $B = \{x |x > 2 m - 1\}$ .

(1)、当 $m = 0$ 时，求 $A \cup B$ ；

(2)、若 $A \cap (∁_{R} B)$ 中整数元素的个数为3，写出 $m$ 的一个值.

查看解析
15、已知函数 $f (x) = \frac{8}{x}$ ， $x \in [1, 2]$ ， $g (x) = a x + 2 a - 1$ ， $x \in [- 1, 3]$ .对于任意的 $x_{1} \in [1, 2]$ ，存在 $x_{2} \in [- 1, 3]$ ，使得 $f (x_{1}) \geq g (x_{2})$ ，则 $a$ 的取值范围是．

查看解析
16、函数 $f (x) = \frac{\sqrt{8 - x}}{3 x - 1}$ 的定义域为．

查看解析
17、若函数 $f (3 x - 1)$ 的定义域为 $(0, 3)$ ，则函数 $f (1 - 3 x)$ 的定义域为（）

A、 $(- 3, 0)$ B、 $(- \frac{2}{3}, \frac{1}{3})$ C、 $(- 1, 8)$ D、 $(- \frac{7}{3}, \frac{2}{3})$

查看解析
18、若函数 $f (x) = \{\begin{array}{l} x^{2} + 1, x \leq 0 \\ \frac{1}{x - a}, x > 0 \end{array}$ ，且 $f (f (- 1)) = \frac{1}{2}$ ，则 $a =$ （）

A、 $- 1$ B、0 C、 $\frac{1}{2}$ D、1

查看解析
19、已知集合 $A = \{0, 1, 4, 6, 7, 8, 10\}$ ， $B = \{x |x = 2 n, n \in N\}$ ，则 $A \cap B$ 中元素的个数为（）

A、3 B、4 C、5 D、6

查看解析
20、“ $\forall x \in Z$ ， $\sqrt{|x|} \in Z$ ”的否定是（）

A、 $\exists x \in Z$ ， $\sqrt{|x|} \in Z$ B、 $\exists x \in Z$ ， $\sqrt{|x|} \notin Z$ C、 $\exists x \notin Z$ ， $\sqrt{|x|} \notin Z$ D、 $\forall x \in Z$ ， $\sqrt{|x|} \notin Z$

查看解析

上一页 819 820 821 822 823 下一页跳转