相关试卷
-
1、设椭圆的左、右顶点分别为 , 右焦点 , .(1)、求椭圆方程及其离心率;(2)、已知点是椭圆上一动点(不与顶点重合),直线交轴于点 , 若的面积是面积的倍,求直线的方程.
-
2、半正多面体(semiregular solid)亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为 , 则( )
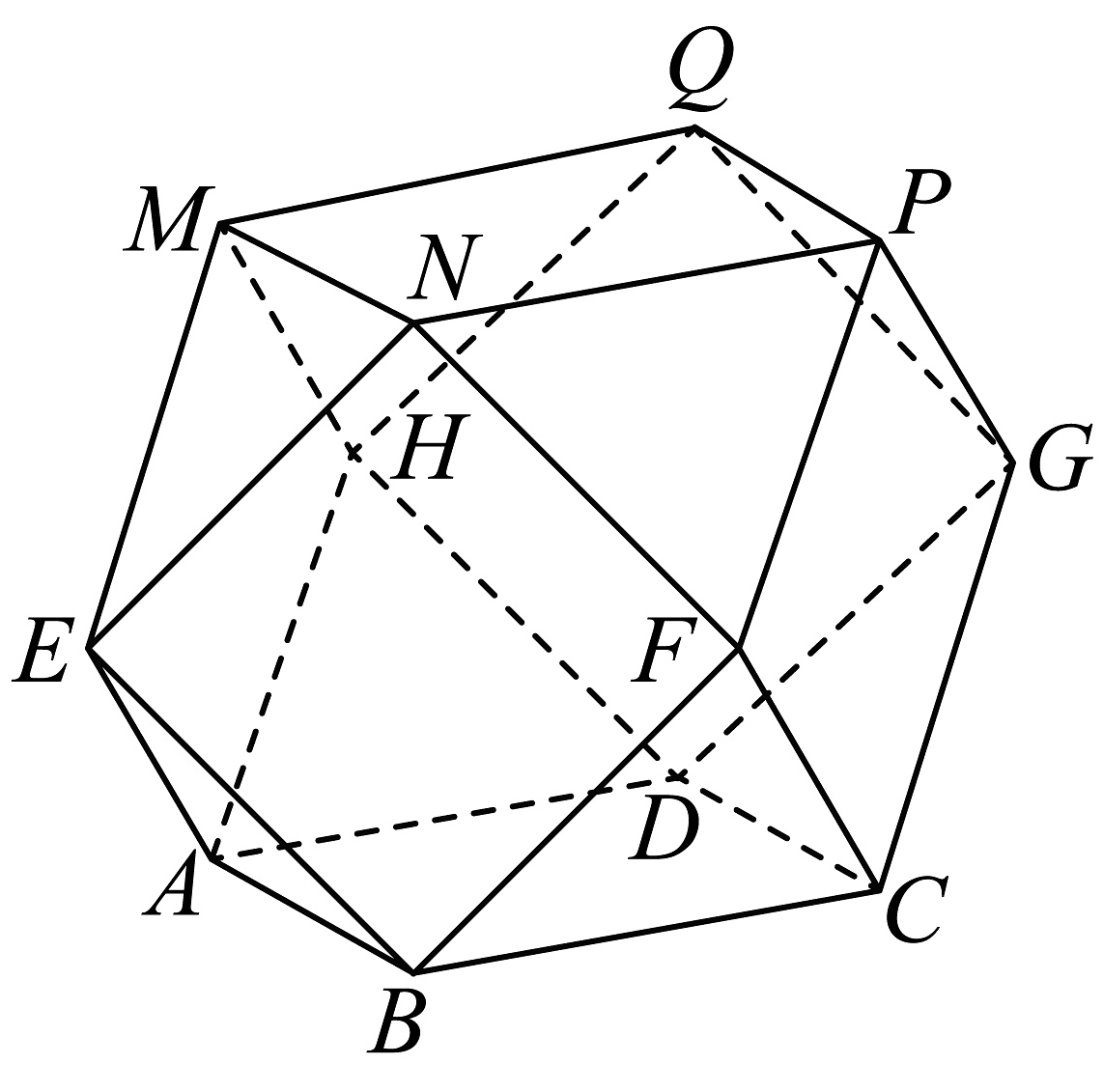 A、平面EAB B、该二十四等边体的体积为 C、该二十四等边体外接球的表面积为 D、PN与平面EBFN所成角的正弦值为
A、平面EAB B、该二十四等边体的体积为 C、该二十四等边体外接球的表面积为 D、PN与平面EBFN所成角的正弦值为 -
3、已知曲线在点处的切线与轴相交于点 , 则实数( )A、-2 B、-1 C、1 D、2
-
4、已知椭圆的左、右顶点为 , , 焦距为.为坐标原点,过点、的圆交直线于、两点,直线、分别交椭圆于、.(1)、求椭圆的方程;(2)、记直线 , 的斜率分别为、 , 求的值;(3)、证明:直线过定点,并求该定点坐标.
-
5、若 , , , 则下列不等式恒成立的是( )A、 B、 C、 D、
-
6、2023年10月26日,中国的神舟十七号载人飞船与“天宫”空间站成功对接,形成三舱三船组合体.某地区为了激发当地人民对天文学的兴趣,开展了天文知识比赛,满分100分(95分及以上为认知程度高),结果认知程度高的有人,这人按年龄分成5组,其中第一组: , 第二组: , 第三组: , 第四组: , 第五组: , 得到如图所示的频率分布直方图.已知第一组有10人.
 (1)、根据频率分布直方图,估计这人的第60百分位数(精确到0.1);(2)、现从第四组和第五组用分层随机抽样的方法抽取6人,担任“党章党史”宣传使者.
(1)、根据频率分布直方图,估计这人的第60百分位数(精确到0.1);(2)、现从第四组和第五组用分层随机抽样的方法抽取6人,担任“党章党史”宣传使者.①有甲(年龄36),乙(年龄42),且甲、乙确定入选,从6人中要选择两个人担任组长,求甲、乙两人至少有一人被选上组长的概率;
②若第四组宣传使者的年龄的平均数与方差分别为36和 , 第五组宣传使者的年龄的平均数与方差分别为42和1,估计这人中35-45岁所有人年龄的平均数和方差.
-
7、某校对2022年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取100名学生,将分数按照 , , , , , 分成6组,制成了如图所示的频率分布直方图:
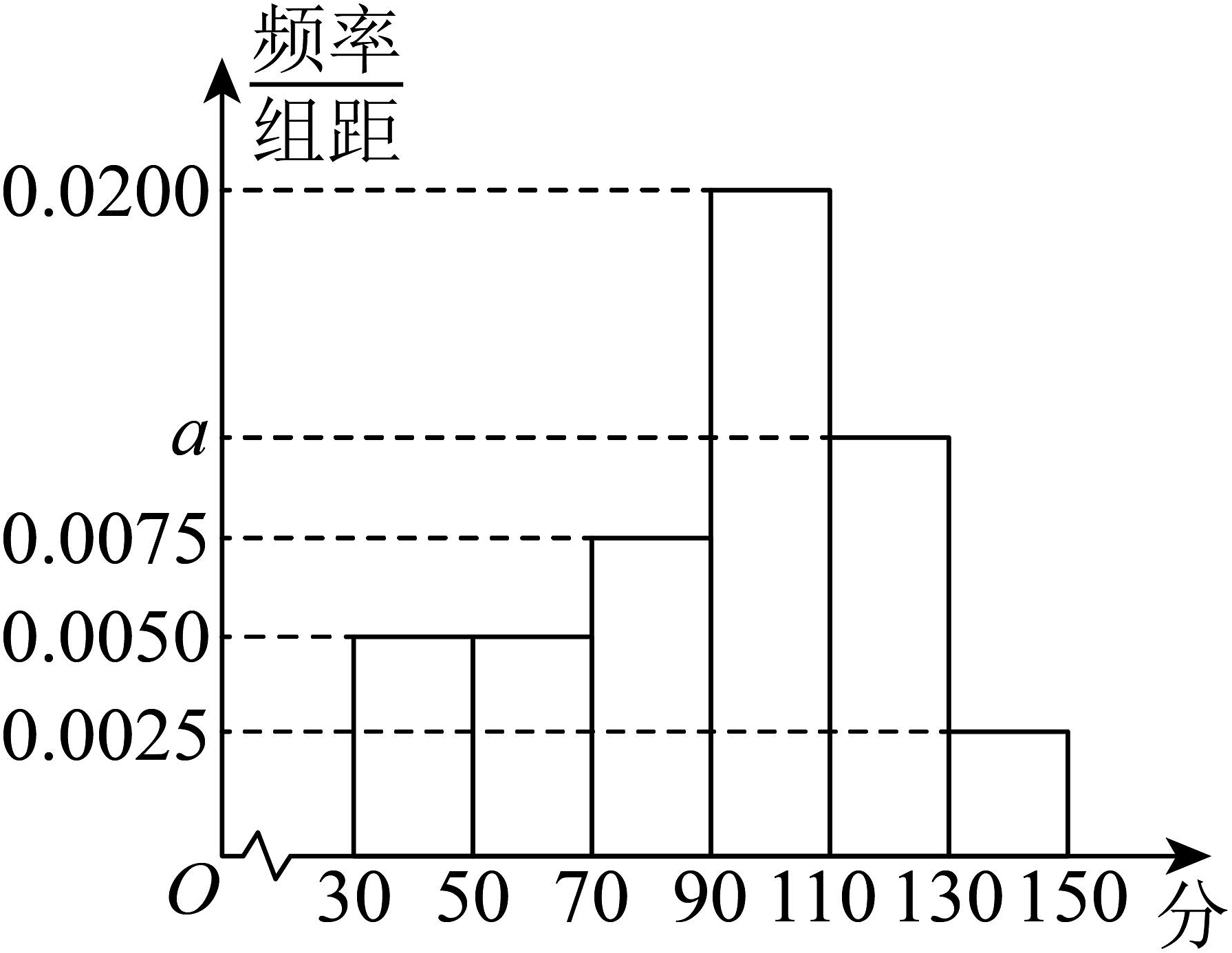
请完成以下问题:
(1)、估计该校高一期中数学考试成绩的平均数;(2)、为了进一步了解学生对数学学习的情况,由频率分布直方图,成绩在和的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在内的概率. -
8、在神舟十五号载人飞行任务取得了圆满成功的背景下.某学校高一年级利用高考放假期间组织1200名学生参加线上航天知识竞赛活动,现从中抽取200名学生,记录他们的首轮竞赛成绩并作出如图所示的频率分布直方图,根据图形,请回答下列问题:
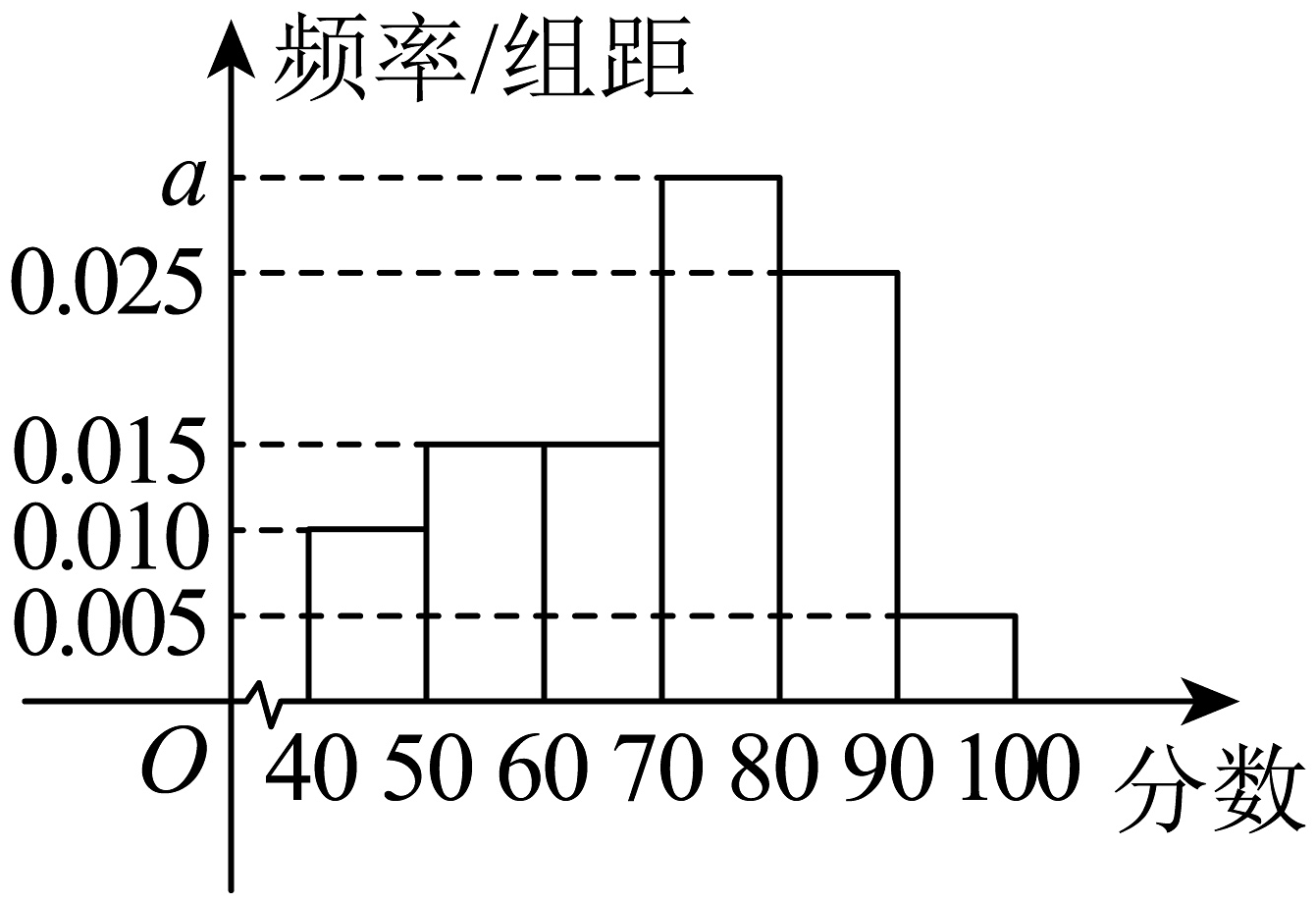 (1)、若从成绩不高于60分的同学中按分层抽样方法抽取10人,求10人中成绩不高于50分的人数;(2)、求的值,并以样本估计总体,估计该校学生首轮竞赛成绩的平均数以及中位数;(3)、由首轮竞赛成绩确定甲、乙、丙三位同学参加第二轮的复赛,已知甲复赛获优秀等级的概率为 , 乙复赛获优秀等级的概率为 , 丙复赛获优秀等级的概率为 , 甲、乙、丙是否获优秀等级互不影响,求三人中至少有两位同学复赛获优秀等级的概率.
(1)、若从成绩不高于60分的同学中按分层抽样方法抽取10人,求10人中成绩不高于50分的人数;(2)、求的值,并以样本估计总体,估计该校学生首轮竞赛成绩的平均数以及中位数;(3)、由首轮竞赛成绩确定甲、乙、丙三位同学参加第二轮的复赛,已知甲复赛获优秀等级的概率为 , 乙复赛获优秀等级的概率为 , 丙复赛获优秀等级的概率为 , 甲、乙、丙是否获优秀等级互不影响,求三人中至少有两位同学复赛获优秀等级的概率. -
9、如图,在四棱锥中,底面四边形是正方形, , 底面 , 是线段的中点,在线段上, .
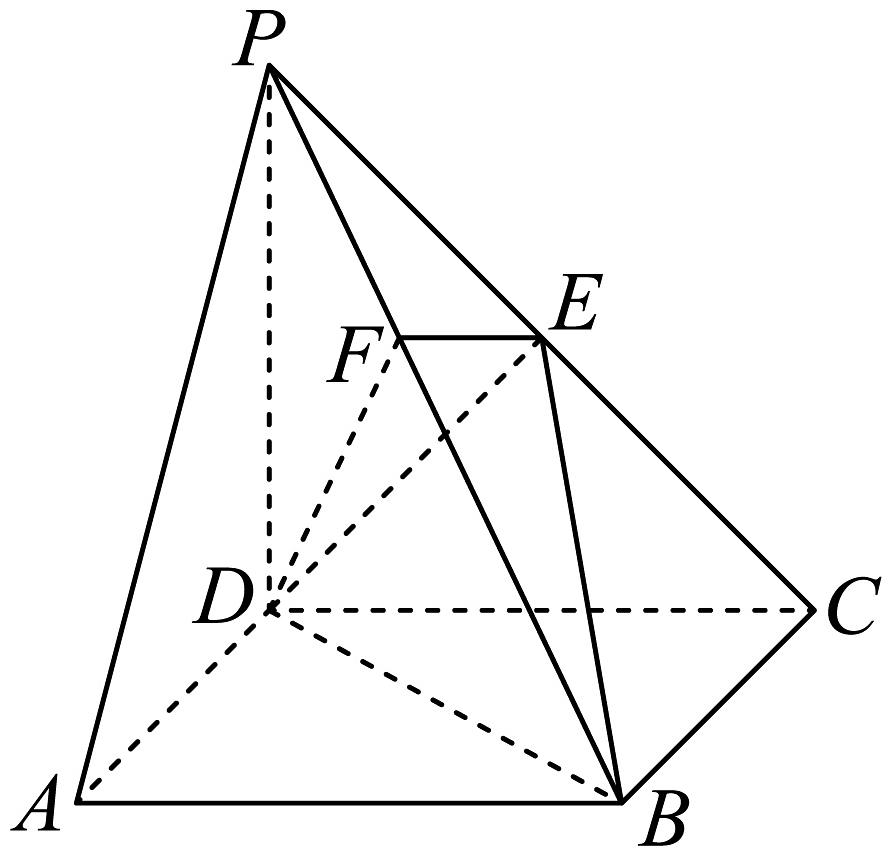 (1)、证明:平面;(2)、在线段上,与所成的角为 , 求平面与平面夹角的余弦值.
(1)、证明:平面;(2)、在线段上,与所成的角为 , 求平面与平面夹角的余弦值. -
10、已知内角的对边分别是 , 则( )A、 B、的最小值为3 C、若为锐角三角形,则 D、若 , 则
-
11、给出下列命题,其中正确的是 ( )A、若是空间的一个基底,则也是空间的一个基底 B、在空间直角坐标系中,点关于坐标平面的对称点是 C、点P为平面ABC上一点,O为平面ABC外一点,且 , 则 D、非零向量 , , 若 , 则为锐角
-
12、已知中,角所对的边分别是 , 向量 , , 且.(1)、求的值;(2)、若 , 求周长的取值范围.
-
13、如图,正三棱锥中, , 点分别为的中点,一只蚂蚁从点出发,沿三棱锥侧面爬行到点 , 求:
 (1)、该三棱锥的体积与表面积;(2)、蚂蚁爬行的最短路线长.
(1)、该三棱锥的体积与表面积;(2)、蚂蚁爬行的最短路线长. -
14、已知复数 , , 则的最大值为.
-
15、已知是方向相同的单位向量,且向量在向量方向上的投影向量为 , 求与的夹角.
-
16、已知函数则下列选项正确的是( )A、函数在区间上单调递增 B、函数的值域为 C、方程有两个不等的实数根 D、不等式解集为
-
17、已知 , , 则下列命题正确的有( )A、若 , 则 B、若 , 则与共线 C、 D、的最大值为3
-
18、如图,在中,是线段上的一点,且 , 过点的直线分别交直线 , 于点 , , 若 , , 则的最小值是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、是函数在上恒大于0的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
20、如图,是水平放置的的直观图, , , 则的面积是( )
 A、 B、 C、 D、
A、 B、 C、 D、