相关试卷
-
1、若 , , 三点共线,则( )A、 B、 C、 D、
-
2、由1,2,3抽出一部分或全部数字所组成的没有重复数字的自然数集合有( )个元素A、15 B、16 C、17 D、18
-
3、在中,内角的对边分别为 , 已知 , , 则外接圆的半径为( )A、1 B、 C、2 D、
-
4、在中, , , , 则等于( )A、45°或135° B、135° C、45° D、30°
-
5、某公司决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.(1)、据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?(2)、为了扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和销售策略调整,并提高定价到x元.公司拟投入万元.作为技改费用,投入50万元作为固定宣传费用,投入万元作为浮动宣传费用.试问:当该商品改革后的销售量至少达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时每件商品的定价.
-
6、已知的不等式: .(1)、 , 求不等式的解集.(2)、 , 求不等式的解集.
-
7、已知集合 , .(1)、若 , 求实数k的取值范围;(2)、已知命题 , 命题 , 若p是q的必要不充分条件,求实数k的取值范围.
-
8、(1)比较与的大小;
(2)已知 , 求证: .
-
9、若对 , 使得成立,则实数的取值范围为 .
-
10、若命题p:“ , ”是假命题,命题q: , , 是真命题,则实数a的取值范围是 .
-
11、集合的真子集的个数是.
-
12、已知 , 则的最小值为( )A、 B、0 C、1 D、
-
13、设集合含有 , 1两个元素,含有 , 2两个元素,定义集合 , 满足 , 且 , 则中所有元素之积为( )A、 B、 C、8 D、16
-
14、“”是“关于的一元二次方程有实数根”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
15、的定义域为( )A、 B、 C、 D、
-
16、在中, , , , 分别是上的点,满足且经过的重心,将沿折起到的位置,使 , 是的中点,如图所示.
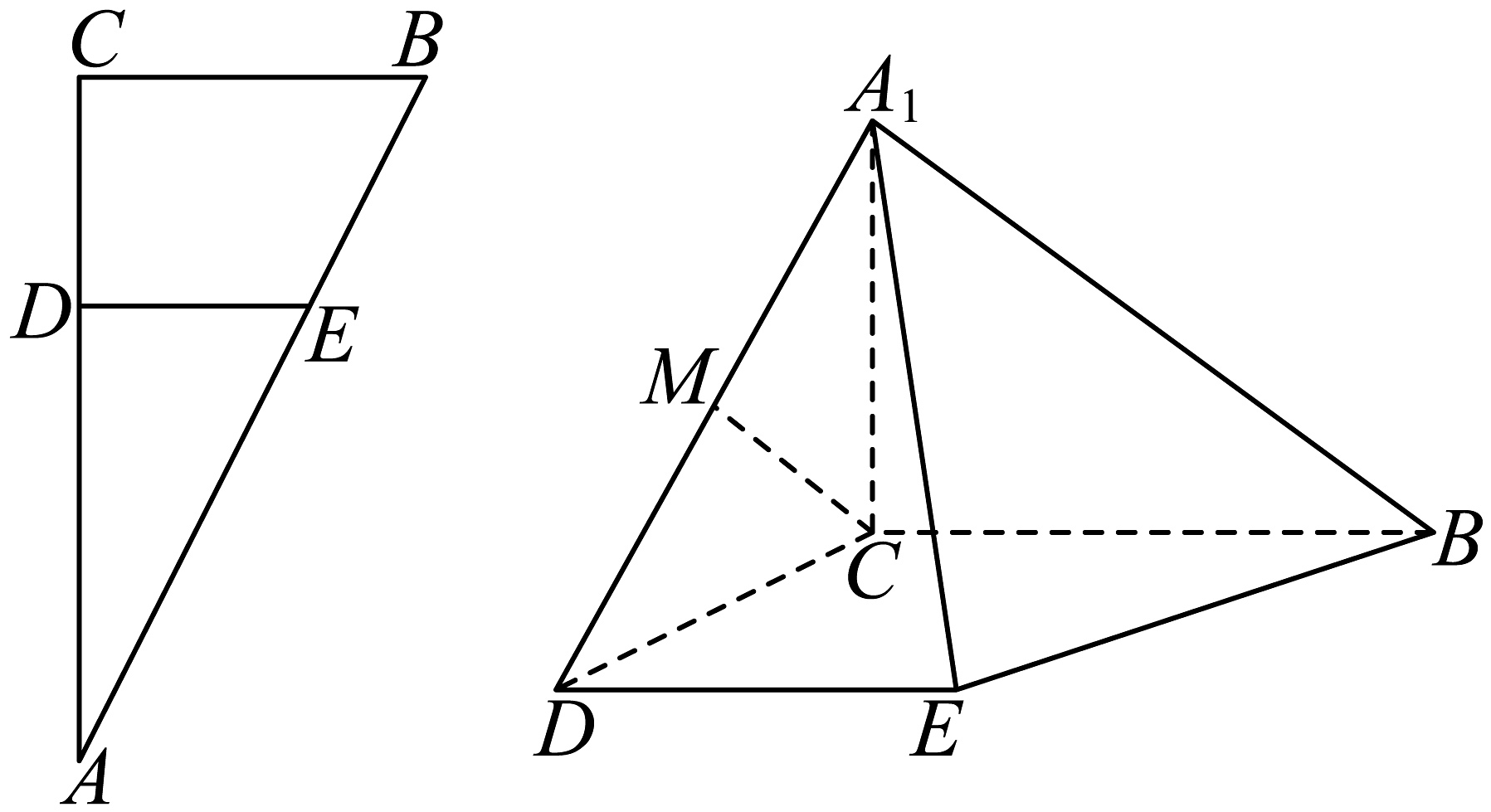 (1)、求证:平面;(2)、求与平面所成角的大小;(3)、在线段上是否存在点 , 使平面与平面成角余弦值为?若存在,求出的长度;若不存在,请说明理由.
(1)、求证:平面;(2)、求与平面所成角的大小;(3)、在线段上是否存在点 , 使平面与平面成角余弦值为?若存在,求出的长度;若不存在,请说明理由. -
17、伯努利试验是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是每次试验只有两种可能结果.若连续抛掷一枚质地均匀的硬币n次,记录这n次实验的结果,设事件M=“n次实验结果中,既出现正面又出现反面”,事件N=“n次实验结果中,最多只出现一次反面”,则下列结论正确的是( ).A、若 , 则M与N不互斥 B、若 , 则M与N相互独立 C、若 , 则M与N互斥 D、若 , 则M与N相互独立
-
18、已知二次函数满足 , 且该函数的图象经过点 , 在x轴上截得的线段长为4,设.(1)、求的解析式;(2)、求函数在区间上的最小值;(3)、设函数 , 若对于任意 , 总存在 , 使得成立,求a的取值范围.
-
19、如图,在四棱锥中,平面ABCD,PB与底面ABCD所成角为 , 底面ABCD为直角梯形,.
 (1)、求PB与平面PCD所成角的正弦值;(2)、求平面PCD与平面PBA所成角的余弦值;(3)、N为AD中点,线段PC上是否存在动点M(不包括端点),使得点P到平面BMN距离为.
(1)、求PB与平面PCD所成角的正弦值;(2)、求平面PCD与平面PBA所成角的余弦值;(3)、N为AD中点,线段PC上是否存在动点M(不包括端点),使得点P到平面BMN距离为. -
20、已知函数 .(1)、求的最小正周期及单调递增区间;(2)、求在区间上的最值,并求出此时对应的的值;(3)、若在区间上有两个零点,直接写出的取值范围.