相关试卷
-
1、若向量 , , 且 , 则.
-
2、已知正方体的棱长为2,分别是棱的中点,下列结论正确的是( )A、 B、直线与直线所成角为 C、三棱锥的体积为 D、过三点的平面截该正方体所得的截面为六边形
-
3、连续抛掷一枚硬币两次,事件表示“第一次硬币正面朝上”,事件表示“第二次硬币反面朝上”,事件表示“两次硬币都正面朝上”,事件表示“两次硬币朝上的情况不同”,则( )A、与相互独立 B、与相互独立 C、与相互独立 D、与相互独立
-
4、已知为复数,为虚数单位,则下列结论正确的是( )A、若 , 则 B、 C、若 , 则为纯虚数 D、若 , 则的最小值为1
-
5、函数()的最大值和最小值是、 , 则的值为( )A、1 B、 C、2 D、
-
6、如图,在四面体中,点在平面上的射影是 , , 若 , 则异面直线与所成角的余弦值为( )
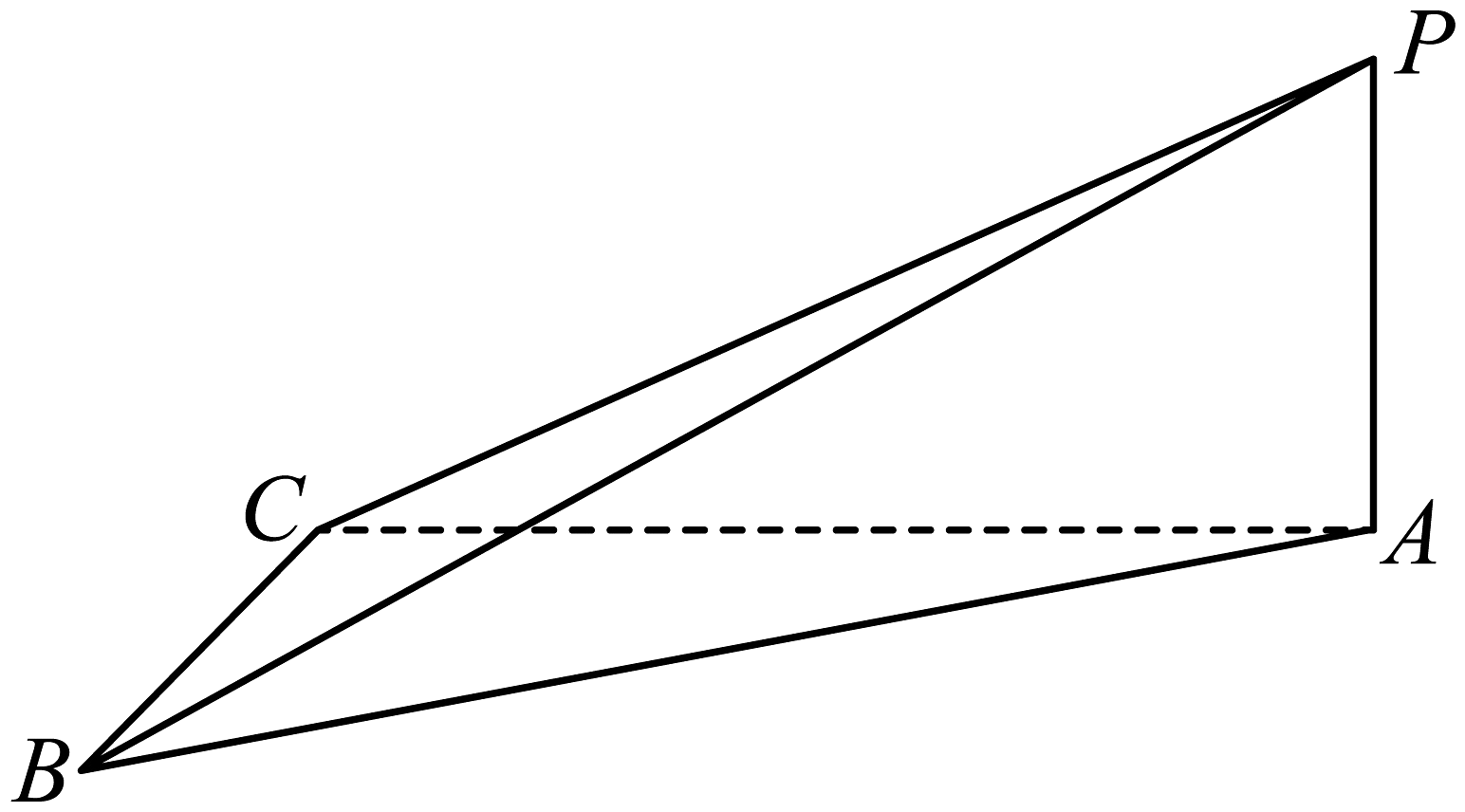 A、 B、 C、 D、
A、 B、 C、 D、 -
7、我国古代数学典籍《九章算术》卷九“勾股”中有一测量问题:“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽,问索长几何?这个问题体现了古代对直角三角形的研究,现有一竖立的木头柱子,高4米,绳索系在柱子上端,牵着绳索退行,当绳索与底面夹角为75°时绳索未用尽,再退行米绳索用尽(绳索与地面接触),则绳索长为( )A、米 B、米 C、米 D、米
-
8、某项比赛共有7个评委评分,若去掉一个最高分与一个最低分,则与原始数据相比,一定不变的是( )A、极差 B、45%分位数 C、平均数 D、众数
-
9、设是定义在上且周期为2的偶函数,当时, , 则( )A、 B、 C、 D、
-
10、在中,若 , , , 则( )A、 B、 C、 D、
-
11、已知复数z与在复平面内对应的点关于虚轴对称,则( ).A、 B、 C、 D、
-
12、若函数是幂函数,则实数的值为.
-
13、现有一批产品,每件产品是否合格相互独立,每件产品合格的概率均为p.在某次抽样中,经统计抽取的100件产品中,恰有98件合格品.(1)、以频率估计概率,若从该批产品中再抽取10件,记合格品的数量为X,求X的期望;(2)、在概率统计中,我们常常通过观测到的实验结果应用极大似然估计法来估计某参数的取值.设X为与未知参数m有关的离散型随机变量,其中m的取值范围为S.若对已知结果 , 存在 , 且对任意 , 有成立,则称为m的一个极大似然估计值.
①请根据此次抽样,求p的极大似然估计值 .
②在实际操作中往往采用多次独立抽样来求参数的极大似然估计值,现对该批产品进行m次独立抽样,每次从中抽取n个产品,记录合格品数分别对应为 , , …, , 请根据这m次独立抽样结果,求p的极大似然估计值 .
-
14、已知函数 , .(1)、讨论的单调性;(2)、若方程有两根,求a的取值范围;(3)、证明:当时, .
-
15、近年来,轻食作为餐饮的一种创新形态,广受消费者青睐.某公司为了获得轻食消费者行为数据,对一地区消费者进行抽样调查.统计其中300名消费者(表中3个年龄段的人数各100人)食用轻食的频数与年龄得到如下的频数分布表.
年龄
食用频数
25岁以下
()
25岁到50岁
50岁及以上
()
轻食低频消费者(每周次)
15
35
50
轻食中频消费者(每周2-3次)
55
45
40
轻食高频消费者(每周4-6次及以上)
30
20
10
(1)、已知该地区25岁以下、25岁到50岁、50岁及以上三个年龄段的人数比例为 , 用频率估计概率,求从该地区随机抽取一人,其为高频消费者的概率.(2)、从以上样本的轻食高频消费者(每周4-6次及以上)中,采用按比例分配的分层随机抽样抽取6人,再从这6人中随机抽取3人,记这3人中年龄在25岁以下与25岁到50岁的人数分别为 , , 记 , 求的分布列与期望. -
16、在科技日新月异的今天,无人驾驶网约车正逐渐成为出行领域的新宠,根据统计数据显示,某区域过去5天的订单数如下:
日期x(天)
1
2
3
4
5
订单数y(件)
13
21
45
55
66
为了进一步了解订单数的变化情况,甲乙两个数学学习小组分别进行了研究,
(1)、甲小组决定用线性回归模型进行拟合,求此时y关于x的经验回归方程;(2)、乙小组采用非线性回归模型进行拟合,求得y关于x的经验回归方程为 , 并计算出决定系数 ,①根据回归模型的决定系数,说明哪个小组的模型拟合效果更好;
②用①中选择的模型预测该区域第10天的订单数(结果保留整数).
附: , ;决定系数 . 参考数据:
-
17、已知函数 .(1)、当时,求曲线在处的切线方程;(2)、若2是的极小值点,求及函数的极值.
-
18、有6张卡片,正面分别写有数字1,2,3,4,5,6,背面均写有数字7.先把这些卡片正面朝上排成一排,且第个位置上的卡片恰好写有数字 . 然后掷一枚质地均匀的骰子,若向上点数为n,则将第n个位置上的卡片翻面并置于原处.进行上述实验3次,发现卡片朝上的数字之和为偶数,在这一条件下,计算骰子恰有一次点数为3的概率为 .
-
19、已知函数 , 若在上单调递增,则实数a的取值范围为 .
-
20、已知 , 那么 .