相关试卷
-
1、已知 , 则 .
-
2、销售甲、乙两种商品所得利润分别是万元,它们与投入资金万元的关系分别为 , (其中都为常数),函数对应的曲线如图所示.
 (1)、求函数与的解析式;(2)、若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值.
(1)、求函数与的解析式;(2)、若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值. -
3、如图所示,在四棱锥中,底面为梯形,且满足 , , , 平面平面.

(1)求证:;
(2)求直线与平面所成角的正弦值.
-
4、已知函数 .
(1)当时,求函数的极值;
(2)当时,若不等式恒成立,求实数的取值范围.
-
5、如图,三棱柱中, , , .

(Ⅰ)证明:;
(Ⅱ)若 , 在棱上是否存在点 , 使得二面角的大小为 , 若存在,求的长,若不存在,说明理由.
-
6、已知二次函数 , 非空集合.(1)、当时,二次函数的最小值为 , 求实数的取值范围;(2)、当__________时,求二次函数的最值以及取到最值时的取值.
在① , ② , ③ , 这三个条件中任选一个补充在(2)问中的横线上,并求解.
(注:如果选择多个条件分别解答,按第一个解答计分.)
-
7、设 , , 若 , 求实数a的取值范围.
-
8、阅读材料:空间直角坐标系中,过点且一个法向量为的平面的方程为;过点且一个方向向量为的直线的方程为 . 利用上面的材料,解决下面的问题:已知平面的方程为 , 直线是平面与的交线,则直线与平面所成角的正弦值为.
-
9、已知一元二次方程的一个根为2,那么另一根为;的值为 .
-
10、对任意都有.数列满足: , 则.
-
11、对于定义在上的任意奇函数 , 均有( )A、 B、 C、 D、
-
12、已知函数极值点的个数为( )A、0 B、1 C、2 D、3
-
13、(1)若 , 求的值;
(2)化简求值:.
-
14、已知抛物线与圆相交于、两点,且.(1)、求抛物线的方程;(2)、若直线与相交于、两点,是的焦点,求的周长.
-
15、如图,在四棱锥中,平面 , 底面为菱形, , , 为 , 中点.
 (1)、求证:平面;(2)、若(),且直线与平面所成角的正弦值为 , 求的值;(3)、在(2)的条件下,若点为直线上一点,求直线与平面所成角正弦值的最大值.
(1)、求证:平面;(2)、若(),且直线与平面所成角的正弦值为 , 求的值;(3)、在(2)的条件下,若点为直线上一点,求直线与平面所成角正弦值的最大值. -
16、已知圆C:关于直线的对称圆的圆心为D,直线l过点 .(1)、若直线l与圆C相切,求直线l的方程;(2)、若直线l与圆D交于A,B两点, , 求直线l的方程.
-
17、如图,在平行六面体中, , , ,
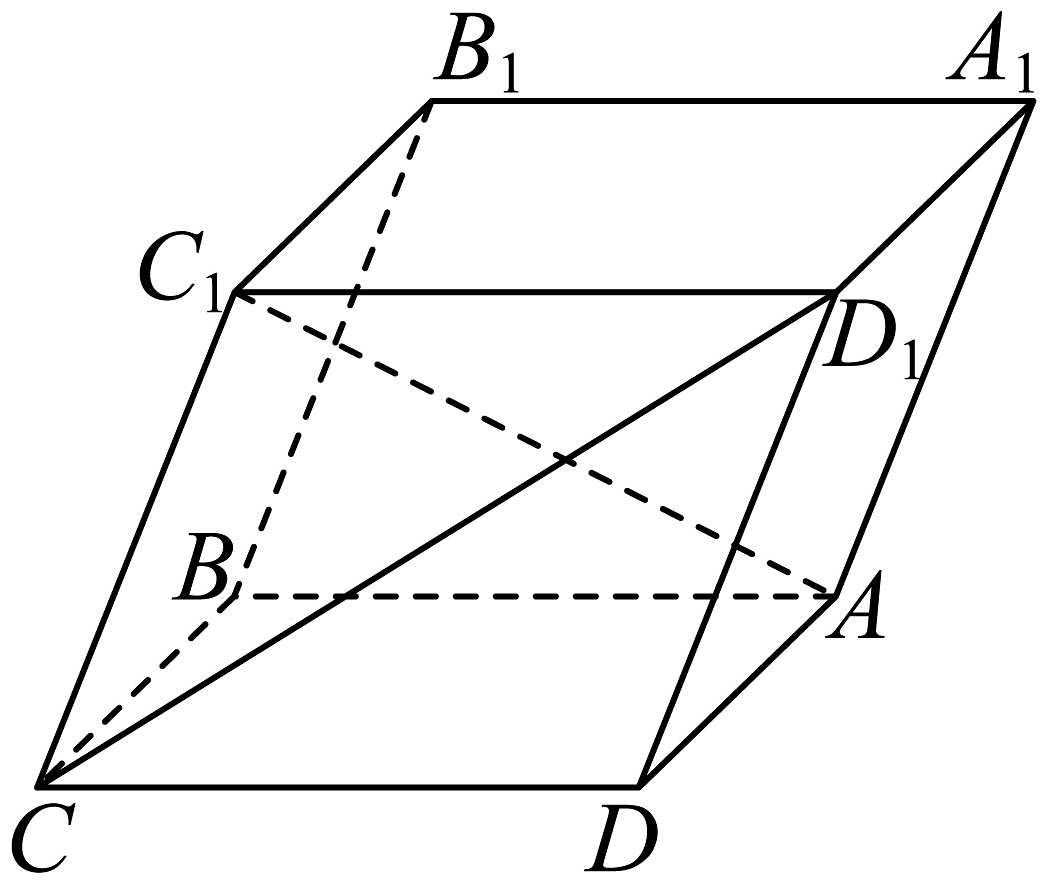 (1)、求的长;(2)、求异面直线与所成角的余弦值.
(1)、求的长;(2)、求异面直线与所成角的余弦值. -
18、若直线的方程为().(1)、若直线与直线m:垂直,求的值;(2)、若直线在x轴上截距是y轴上截距的2倍,求该直线的方程.
-
19、已知 , M是椭圆上的动点, , 分别是其左右焦点,则的最大值为 .
-
20、在棱长为的正方体中,为的中点,则点到平面的距离为.