相关试卷
-
1、已知函数 .(1)、当时,求函数的极值点个数;(2)、若对 , 恒成立,求实数a的取值范围.
-
2、如图,三棱柱中, , , 平面平面 , D为棱的中点, .
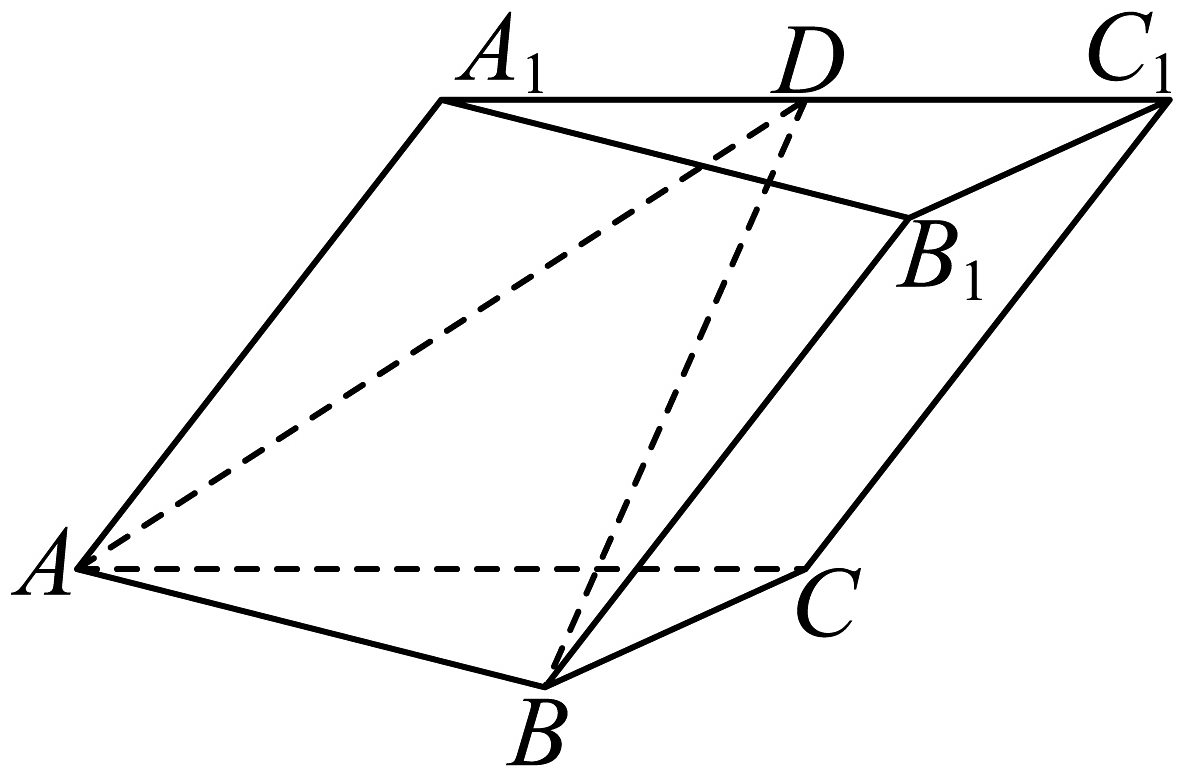 (1)、证明:;(2)、求平面ABD与平面夹角的余弦值.
(1)、证明:;(2)、求平面ABD与平面夹角的余弦值. -
3、固态电池是纯电动汽车搭载的新一代电池,与使用电解液的传统液态锂离子电池相比,固态电池具有安全性能高、能量密度大等特点.某公司试生产了一批新型固态电池,为了了解该批次固态电池的“循环寿命”x(循环寿命是指:电池的容量下降到初始容量的某一阈值时,完成充放电循环的次数)的情况,从这批固态电池中随机抽取了100组进行了测试,并统计绘制了下表:
循环寿命x(千次)
组数y
5
15
a
b
5
已知循环寿命x(千次)的平均值(同一组中的数据用该组区间的中点值代表).
(1)、求a,b的值;(2)、根据测试数据可以认为“循环寿命”x近似服从正态分布 , 经计算样本标准差s的估计值为0.7.用样本数据的平均值作为的值,用样本标准差s的估计值作为的值.(ⅰ)若规定:循环寿命的电池为一等品;的电池为优等品.求试生产的电池的一等品率和优等品率的估计值(结果用百分数表示);
(ⅱ)在该型电池的生产中,称发生概率低于0.27%的事件为小概率事件,在质量控制时,如果小概率事件未发生,则认为该批产品合格;否则可以认为该批产品不合格.若这100组电池中,循环寿命x的最大值和最小值分别为6.5和2.3.请判断该批固态电池是否合格?并说明理由.
参考数据:若随机变量 , 则 , , .
-
4、已知函数的值域为D,集合 , 若 , 则实数a的最大值为 .
-
5、将圆周率的近似值的各个数位上的数字重新排列后得到5位小数M(包括T),则的概率为 .
-
6、已知直线与抛物线相交于A,B两点,D为抛物线的准线与y轴的交点,若的面积为4,则 .
-
7、超椭圆(superellipse)也称为Lamé曲线,是一种类似于椭圆的封闭曲线,保留了椭圆的长轴、短轴、对称性等特点.超椭圆在平面直角坐标系中的方程为( , , ),当 , 时,该超椭圆即为著名的“星形线”,记为曲线C(如图),已知点在曲线C上,O为坐标原点,点为曲线C上任意一点.则下列结论正确的是( )
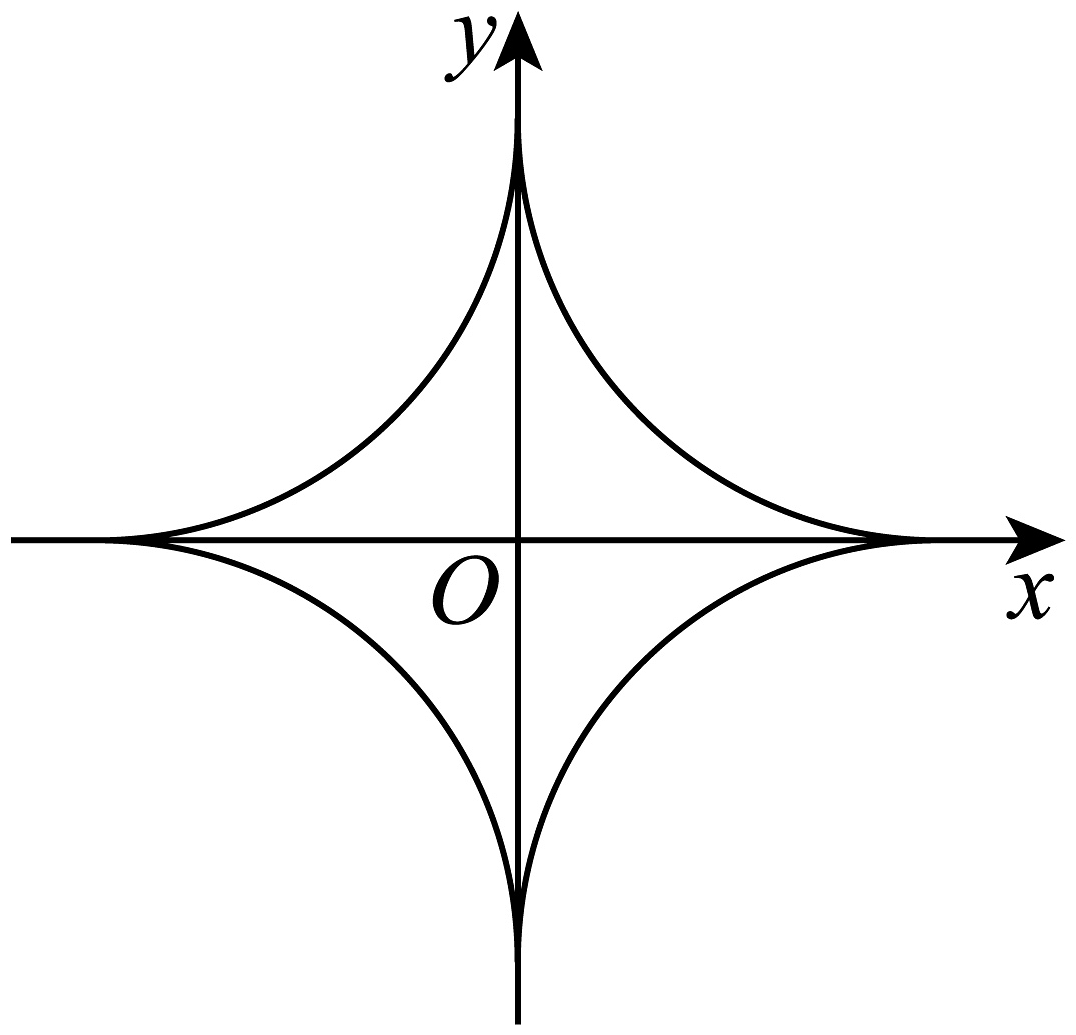 A、 B、的最大值为 C、的最小值为 D、直线与曲线C恰有3个公共点
A、 B、的最大值为 C、的最小值为 D、直线与曲线C恰有3个公共点 -
8、如图,在棱长为4的正方体中,分别为棱 , 底面的对角线上的动点,且 , 则下列结论正确的是( )
 A、三棱锥的体积为 B、平面 C、存在实数 , 使得 D、若直线与平面所成角的正弦值为 , 则
A、三棱锥的体积为 B、平面 C、存在实数 , 使得 D、若直线与平面所成角的正弦值为 , 则 -
9、已知复数 , (),则下列结论正确的是( )A、若 , 则为纯虚数 B、若 , 则在复平面内对应的点位于第一象限 C、若 , 则 D、若 , 为方程()的两虚根,则
-
10、在锐角中,内角A,B,C的对边分别为a,b,c,若 , 则的取值范围为( )A、 B、 C、 D、
-
11、已知数列中, , 且 , 记数列的前项和为 , 则( )A、 B、 C、 D、
-
12、若圆与圆(a,)有且仅有一条公切线,则从点到圆的切线长为( )A、1 B、 C、 D、2
-
13、若函数( , )的最小正周期为 , 其图象的一条对称轴的方程为 , 则函数在上的零点个数为( )A、1 B、2 C、3 D、4
-
14、已知随机事件A,B发生的概率分别为 , , 且 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
15、已知函数为奇函数,则( )A、 B、 C、 D、2
-
16、已知向量 , , 若 , 则( )A、 B、 C、 D、
-
17、已知全集 , 集合 , , 则( )A、 B、 C、 D、
-
18、已知圆为坐标原点,过上任意一点作圆的切线.(1)、若与椭圆相交于两点,证明:;(2)、若与椭圆相交于两点,恒有 , 判断是否过定点?请说明理由.
-
19、已知函数.(1)、设为的导函数,求在上的最小值;(2)、令 , 证明:当时,在上.
-
20、记为数列的前项和, .(1)、求和的通项公式;(2)、设数列的前项和为 , 证明: .