相关试卷
-
1、函数与的图象在区间上的交点个数为( )A、3 B、5 C、7 D、9
-
2、已知数列是以1为首项,2为公差的等差数列,则数列的前10项和为( )A、 B、 C、 D、
-
3、若 , 则( )A、 B、 C、 D、
-
4、如图,网格纸上小正方形的边长为1,向量的起点和终点均在格点上,则向量在向量上的投影向量为( )
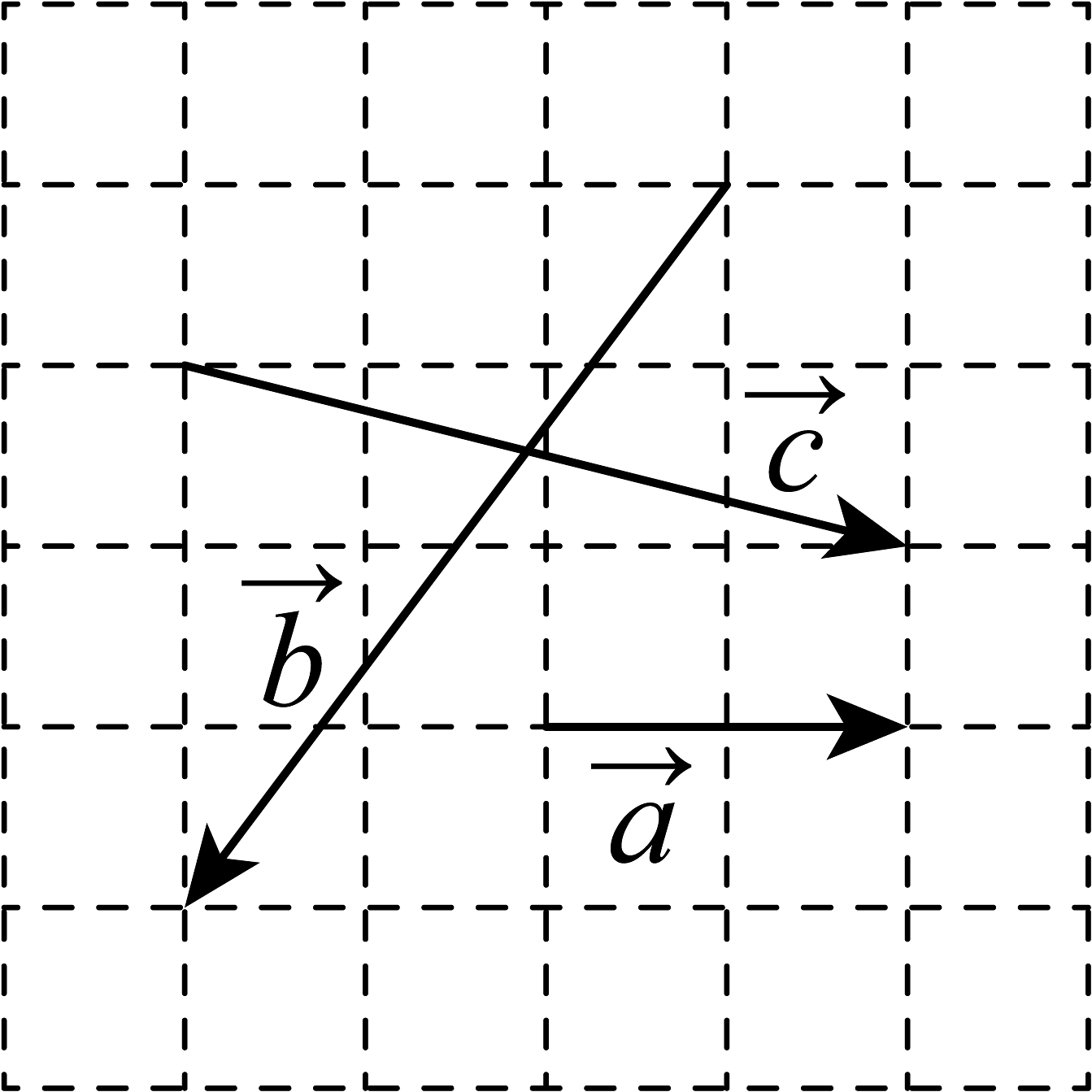 A、 B、 C、 D、
A、 B、 C、 D、 -
5、已知函数且 , 则( ).A、. B、. C、2. D、4.
-
6、若 , 则( )A、 B、1 C、 D、
-
7、已知集合 , 则( )A、 B、 C、 D、
-
8、已知某篮球队有五名队员,其中甲是主要得分手,乙是组织后卫.如果球在乙手中,则他传球给甲的概率为 , 传球给其他队员的概率均为;如果球不在乙手中,则这名队员传球给任何队友的概率都是.开始进攻时,球在乙手中.(1)、求经过2次传球并由甲执行投篮的条件下,球有经过丙之手的概率;(2)、经过次传球后,球回到乙手中的概率;(3)、记经过次传球后,球到甲的手中的概率为 , 求证:满足的的个数不少于满足的的个数.
-
9、函数 , 其中 , .(1)、求函数的单调递增区间;(2)、若 , 函数有且只有一个零点,求实数的取值范围;(3)、若 , , , 求证:.
-
10、如图,在四棱锥中,底面是平行四边形,平面 , , 为的中点,.
 (1)、证明:平面平面;(2)、若 , 求平面与平面所成的锐二面角的余弦值.
(1)、证明:平面平面;(2)、若 , 求平面与平面所成的锐二面角的余弦值. -
11、已知双曲线的一条渐近线方程为 , 过点的直线与双曲线的右支于、两点,点分别为双曲线的左顶点和右焦点,且到渐近线的距离为1,为直角三角形.(1)、求双曲线的方程;(2)、求的面积.
-
12、为了研究大气污染物浓度的影响因素,研究人员检测了经济发展水平相当的24个城市的汽车流量.得到数据如下:
浓度(单位:)
汽车流量(单位:千辆/24小时)
合计
8
2
10
1
13
14
合计
9
15
24
(1)、判断是否有的把握认为浓度与汽车流量有关?(2)、对于随机事件 , , 若 , 则认为事件对事件发生有促进作用,否则就认为是抑制作用.现记为“浓度超过”,为“城市汽车流量不超过1.4千辆/24小时”,用表格数据估计事件A、B发生的概率,试问:事件B对事件A是促进作用还是抑制作用?附: ,
0.050
0.010
0.001
3.841
6.635
10.828
-
13、已知椭圆 , 抛物线 , 点是与在第一象限的交点,是的左顶点,直线交于点 , 若点恰为线段的中点,则的值为.
-
14、老师从10篇课文中随机抽3篇让学生背诵,背诵篇数没达到2篇的为不合格,不合格者积分扣1分;能背诵篇数2篇的为合格,不扣分也不加分;3篇都能背诵的为优秀,优秀者积分加2分,某位同学只能背诵其中的6篇课文,记该同学的得分为 , 则.
-
15、已知复数 , 则的虚部为.
-
16、已知函数 , , 下列结论正确的是( )A、曲线在点(1,2)处的切线方程为 B、函数在区间上存在最小值,则实数的取值范围为(-3,0) C、若曲线与有三个交点 , , , 则 , , 必成等差数列 D、存在曲线与有三个交点 , , , 使得 , , 成等比数列
-
17、已知在等差数列的前项和为 , 其中 , , 在等比数列中, , , 则( )A、 B、数列是等差数列 C、数列的前项和为 D、数列的前项和为
-
18、已知袋中有除颜色外其他都相同的小球9个,其中黑球6个,红球3个,从中摸4个球,方案一:有放回地摸球,记取得红球个数为;方案二:不放回地摸球,记取得红球个数为.下列说法中,正确的有( )A、 B、 , 其中 C、 D、
-
19、已知在三棱锥中, , , 则该三棱锥的外接球表面积为( )A、 B、 C、 D、
-
20、现有8名社工,参加两个社区工作,每个社区4人,其中甲、乙、丙、丁四人是好友关系。他们希望在工作时,至少有一名好友相伴,试问:这样的工作安排方案共( )有种?A、20 B、38 C、70 D、74