相关试卷
-
1、在四棱锥中,面面 , , , , , .
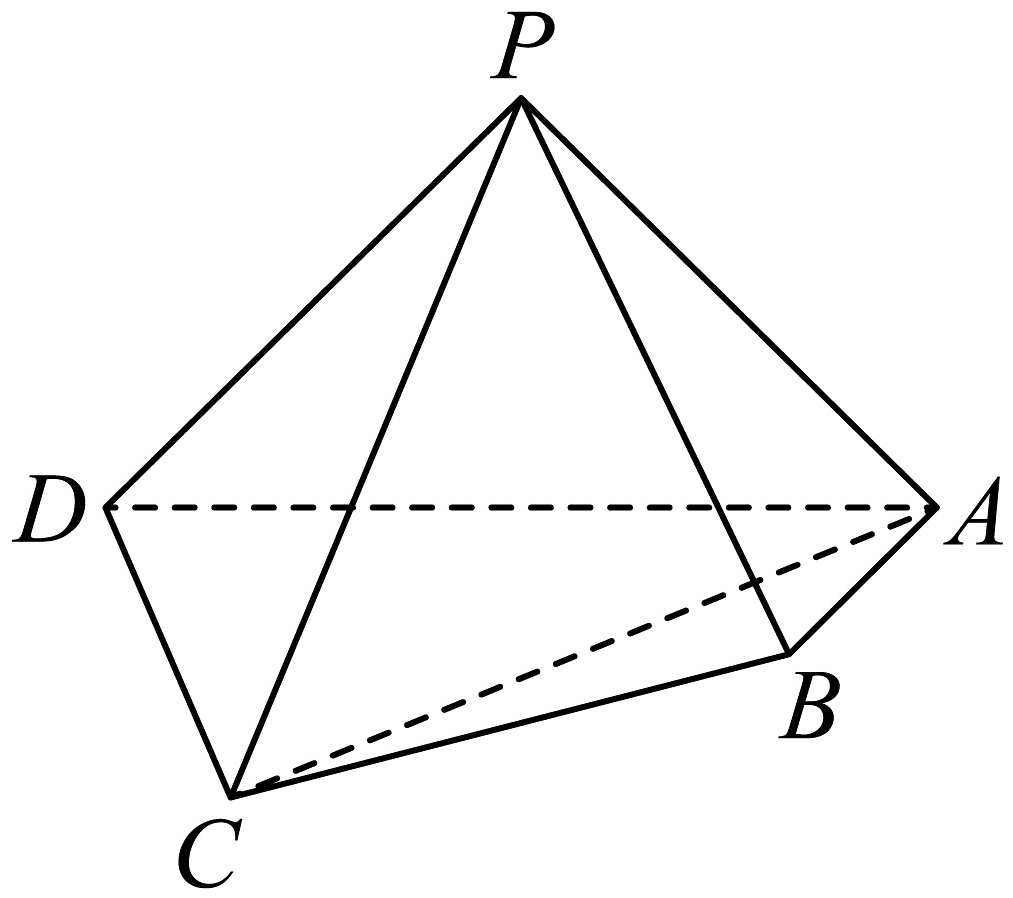 (1)、求证:平面平面;(2)、在棱上是否存在点 , 使得平面?若存在,求的值;若不存在,说明理由.
(1)、求证:平面平面;(2)、在棱上是否存在点 , 使得平面?若存在,求的值;若不存在,说明理由. -
2、设三个内角的对边分别为 , 且 , , 为锐角三角形,是边的中点,则的取值范围是 .
-
3、已知两平行直线的方向向量分别为 , , 则实数的值为 .
-
4、在棱长为的正方体中,已知分别为线段 , 的中点,点满足 , , , 则( )A、当时,三棱锥的体积为 B、当时,四棱锥外接球半径为 C、周长的最小值为 D、若 , 则点的轨迹长为
-
5、先后两次抛掷一枚质地均匀的骰子,得到向上的点数分别为 , 设事件“”,事件“”,事件“为奇数”,则( )A、 B、 C、与相互独立 D、与相互独立
-
6、截角四面体是一种半正八面体,可由四面体经过适当的截角而得到.如图所示,将棱长为6的正四面体沿棱的三等分点作平行于底面的截面截角,得到所有棱长均为2的截角四面体,则截角四面体各个面所在平面中,两个平面是相交平面的概率为( )
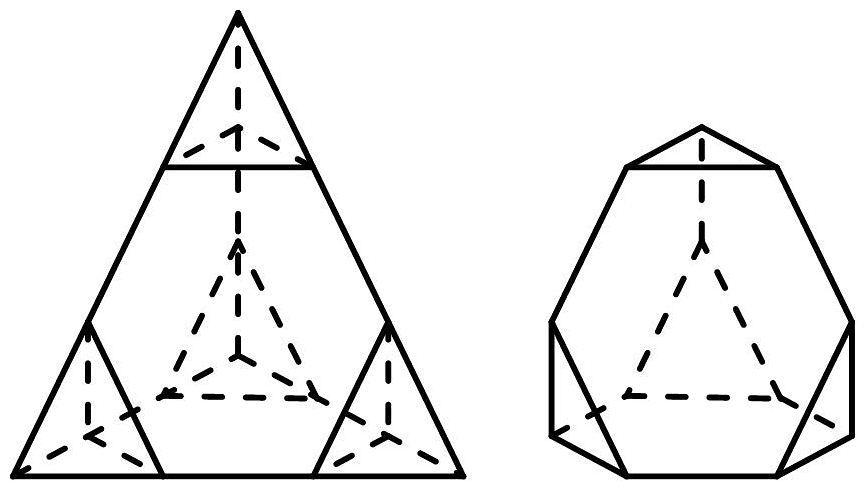 A、 B、 C、 D、
A、 B、 C、 D、 -
7、已知事件互斥,它们都不发生的概率为 , 且 , 则( )A、 B、 C、 D、
-
8、将除颜色外完全相同的2个红球和1个白球随机放入2个不同的盒子中,每个盒子中至少放入1个球,则2个红球分别放入不同盒子中的概率为( )A、 B、 C、 D、
-
9、设函数的定义域为.若实数满足对任意的 , 都有 , 则称满足性质.(1)、若函数满足性质,求实数的取值范围.(2)、设的导函数为 , 且对任意的 , 都有.
(i)证明:满足性质.
(ii)已知数列满足 , 若 , 证明:.
-
10、已知抛物线 , 过抛物线上一点作两条直线分别交抛物线于两点,直线的斜率分别为 , 且.(1)、求抛物线的方程.(2)、证明:直线过定点.(3)、记直线经过的定点为为直线上一点(异于点),且满足 , 证明点在某定直线上,并求出该定直线的方程.
-
11、如图所示,在边长为2的正方体中,分别是棱上的点(异于端点),且 .
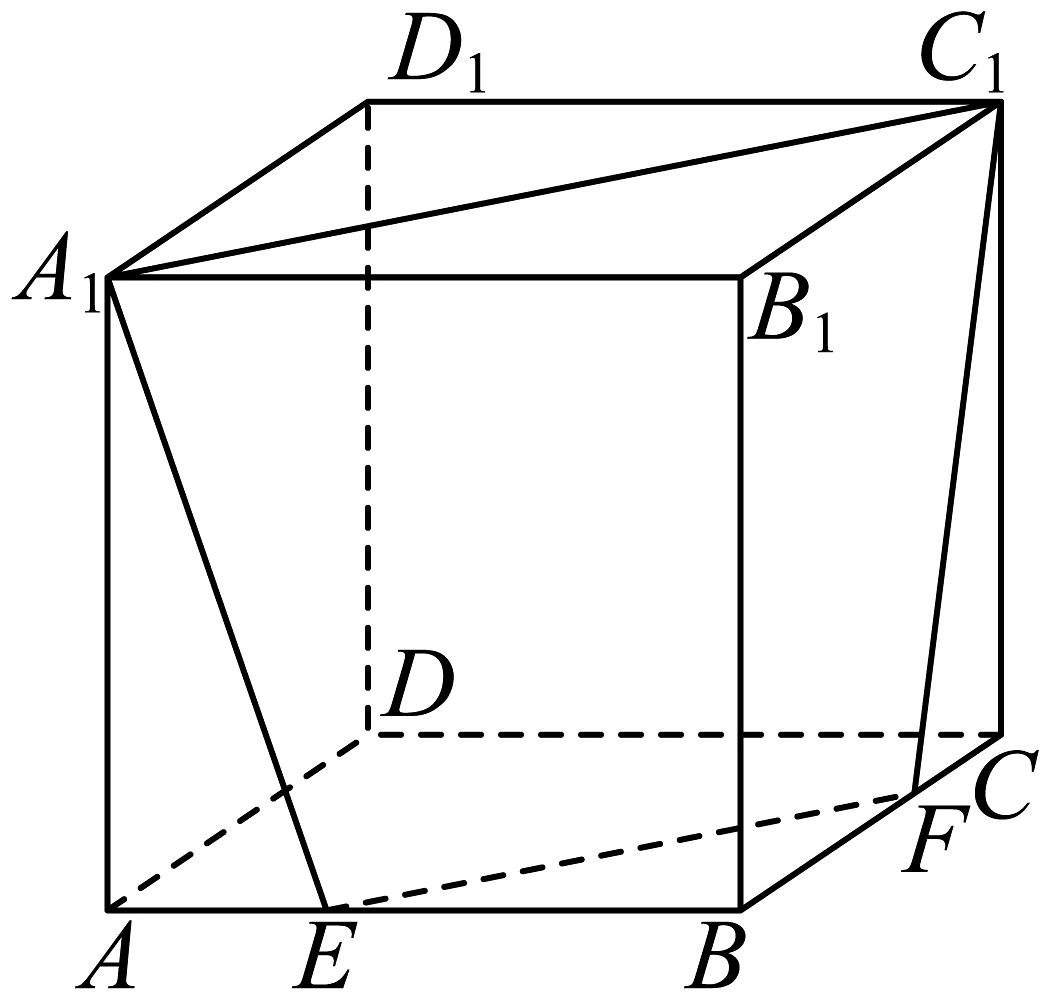 (1)、证明:与相交且交点在直线上.(2)、当直线与平面所成角的正弦值为时,求的值.
(1)、证明:与相交且交点在直线上.(2)、当直线与平面所成角的正弦值为时,求的值. -
12、某学校高三年级组织了一场校内知识挑战赛,共有5个班级参与,每个班级推选1名学生代表参加,其中1名学生代表来自A类班级,4名学生代表来自B类班级,学生甲是B类班级代表之一.在某一轮比赛中,随机选择两名学生代表进行比赛.若是同类班级代表比赛,则双方获胜的概率均为;若是A类班级代表与B类班级代表比赛,则B类班级代表获胜的概率为.(1)、已知学生甲参赛,求在一轮比赛中,学生甲获胜的概率;(2)、若每两个班级代表各进行一轮比赛,记B类班级代表甲获胜的轮数为 , 求的分布列与期望.
-
13、在中,内角所对的边分别为 , 且.(1)、证明:.(2)、求.(3)、若为上靠近点的三等分点,作交于点 , 求.
-
14、现从一含10个元素的集合的子集中随机选出2个不同的子集,被选出的子集之间必须满足包含或被包含的关系,则满足该选取条件的选法有种.
-
15、函数的最小值为.
-
16、已知是椭圆上的动点, , 且 , 则.
-
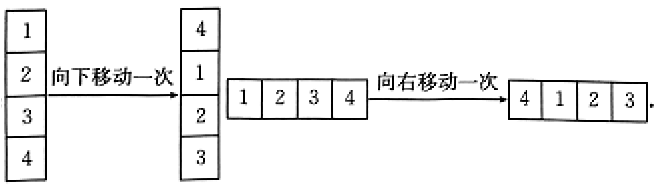
17、如图,在的方格中,移动规则如下:每行均可左右移动,每列均可上下移动,每次仅能对某一行或某一列进行移动,其他行或列不变化.
例如:
4
4
1
3
4
3
2
1
1
2
3
2
2
1
4
3
下列的方格中,哪些图形可由上图经过4次移动得到( )
A、
B、4
4
1
3
4
3
2
1
1
2
3
2
2
1
4
3
C、4
2
4
3
1
1
1
1
2
4
2
2
4
3
3
3
D、3
4
4
4
1
3
1
1
2
2
2
2
4
1
3
3
4
4
1
3
4
3
4
1
3
2
1
2
2
1
2
3
-
18、如图,在圆柱中,轴截面是边长为2的正方形,是以为直径2的圆上一动点(异于点),与圆柱的底面圆交于点 , 则( )
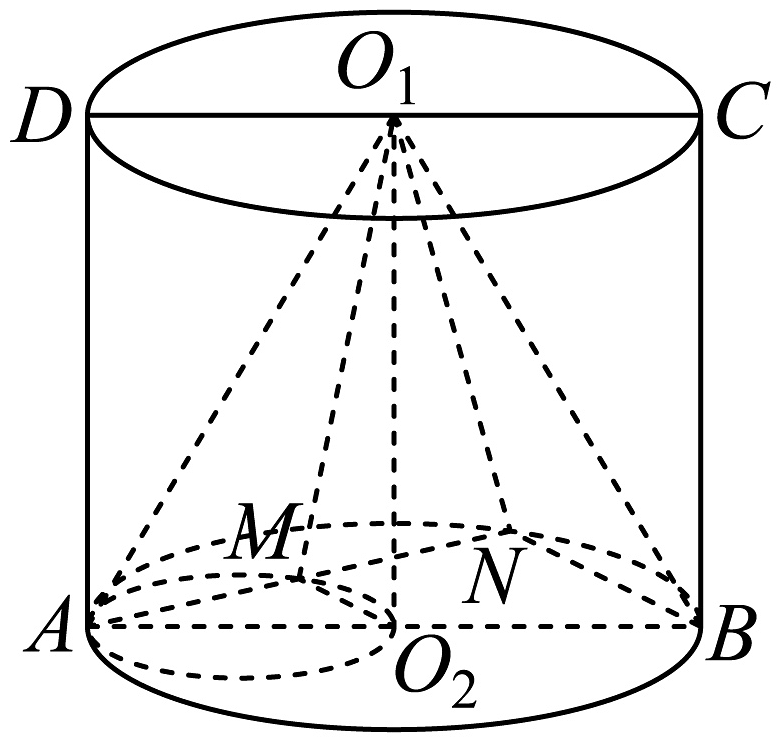 A、平面 B、平面平面 C、直线与直线有可能垂直 D、三棱锥的外接球体积为定值
A、平面 B、平面平面 C、直线与直线有可能垂直 D、三棱锥的外接球体积为定值 -
19、某研究机构在训练人工智能模型时,有两种训练算法甲和乙,使用算法甲训练了30次,每次训练耗时的平均数为2,方差为0.25,使用算法乙训练了20次,每次训练耗时的平均数为1.5,方差为0.3,则( )A、总体每次训练平均耗时1.8小时 B、总体每次训练平均耗时1.75小时 C、总体每次训练耗时的方差为0.28 D、总体每次训练耗时的方差为0.33
-
20、如图,分别为双曲线的左、右焦点,点都在双曲线上,四边形为等腰梯形,且 , , 则双曲线的离心率为( )
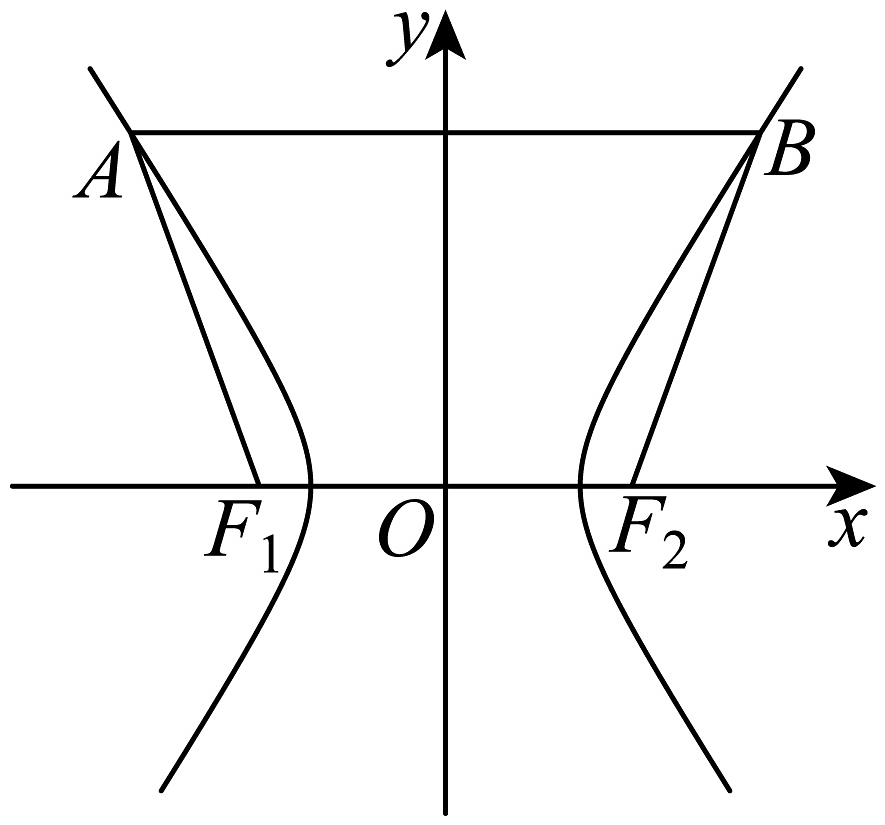 A、 B、 C、2 D、
A、 B、 C、2 D、