相关试卷
-
1、下列说法中正确的是( )A、样本数据3,4,5,6,7,8,9的第80百分位数是 B、随机变量 , 若 , 则 C、已知随机事件A,B,且 , , 若 , 则事件A,B相互独立 D、已知变量x,y具有线性相关关系,其经验回归方程为 , 若样本中心点为 , 则实数m的值为
-
2、甲、乙两人进行局羽毛球比赛(无平局),每局甲获胜的概率均为 , 规定:比赛结束时获胜局数多的人赢得比赛,记甲赢得比赛的概率为 , 假设每局比赛互不影响,则( )A、 B、 C、 D、单调递减
-
3、随机变量的分布列为 , 若 , 则( )A、4 B、3 C、2 D、1
-
4、已知 , , 且 , 则下列选项中不正确的是( )A、 B、 C、 D、
-
5、随机变量的分布列如表所示,则的最大值是( )
0
A、 B、 C、 D、 -
6、下列说法中,正确的命题是( )A、已知随机变量X服从正态分布 , 则 B、线性相关系数r越大,两个变量的线性相关性越强,反之,线性相关性越弱 C、若样本数据的方差为8,则数据的方差为2 D、已知两个变量具有线性相关关系,其回归方程为 , 若 , 则
-
7、空间直角坐标系中,任何一个平面的方程都能表示成(其中均为常数,),为该平面的一个法向量.已知球的半径为4,点均在球的球面上,以所在直线分别为轴建立空间直角坐标系 , 如图所示.平面内的点在球面上,点在轴上的投影在轴的正半轴上, , 过直线作球的截面 , 使得平面平面 , 设截面与球球面的交线为圆(为线段的中点).
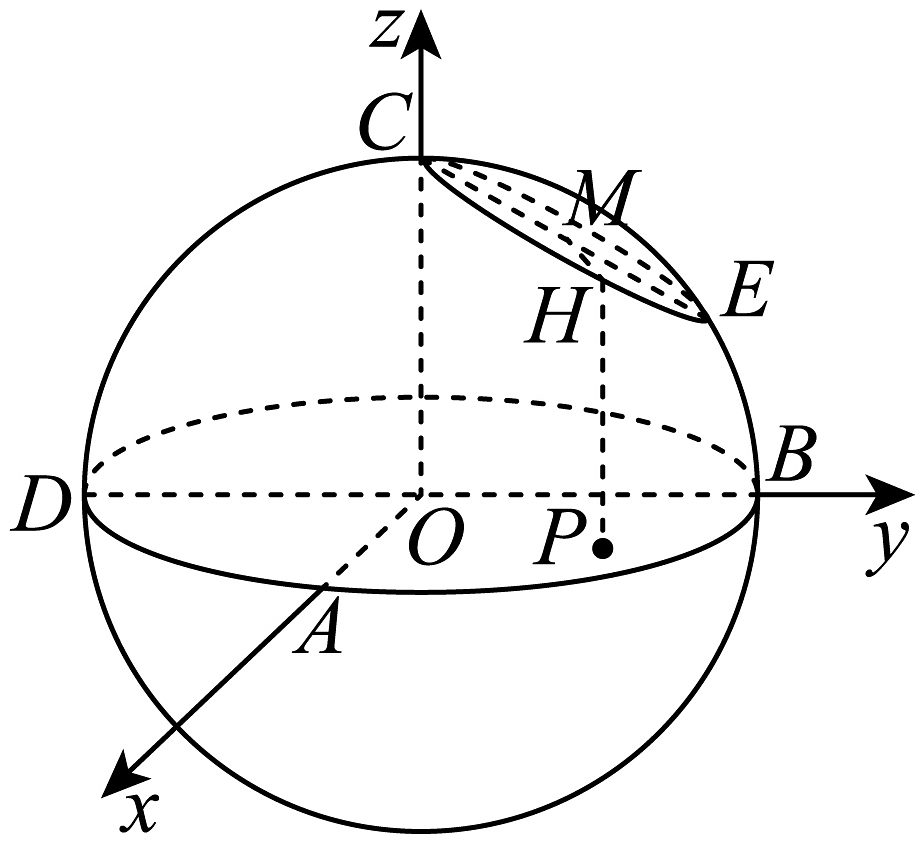 (1)、求点的坐标.(2)、若平面 , 证明:平面平面.(3)、已知点在平面内,设线段在平面内绕着点逆时针旋转弧度至 , 点在圆上,且 , 过作平面 , 垂足为点.
(1)、求点的坐标.(2)、若平面 , 证明:平面平面.(3)、已知点在平面内,设线段在平面内绕着点逆时针旋转弧度至 , 点在圆上,且 , 过作平面 , 垂足为点.①用表示点的坐标;
②若 , 求点到平面距离的最大值;
③若 , 当直线与平面所成的角最小时,求的值.
-
8、已知函数.(1)、当时,求的单调区间;(2)、当时,求在上的最小值;(3)、当时,讨论的零点个数.
-
9、已知椭圆过点为椭圆的左顶点,为坐标原点.(1)、求椭圆C的标准方程;(2)、设为椭圆上的点,线段交轴于点 , 线段交轴于点 , 且 , 求.
-
10、某兴趣小组调查了某校100名学生100米短跑成绩的情况,其中有60名学生的短跑成绩合格.这100名学生中有45名学生每周的锻炼时间超过5小时,60名短跑成绩合格的学生中有35名学生每周的锻炼时间超过5小时.(1)、根据所给数据,完成以下表格,依据小概率值的独立性检验,是否可以推断学生短跑成绩合格与每周的锻炼时间超过5小时有关?
单位:人
每周的锻炼时间
短跑成绩
合计
短跑成绩合格
短跑成绩不合格
每周的锻炼时间超过5小时
每周的锻炼时间不超过5小时
合计
(2)、正确的跑步姿势和起跑技巧等都可以让跑步者更好地发挥自己的能力.现对短跑成绩不合格的学生进行跑步技巧培训,已知每周的锻炼时间超过5小时的学生参加跑步技巧培训后,学生的短跑成绩合格的概率为 , 每周的锻炼时间不超过5小时的学生参加跑步技巧培训后,学生的短跑成绩合格的概率为.用频率代替概率,从短跑成绩不合格的学生中随机抽取1名学生(记为甲)进行跑步技巧培训,求学生甲参加培训后短跑成绩合格的概率.参考公式与数据: , 其中.
0.01
0.005
0.001
6.635
7.879
10.828
-
11、在中,内角所对的边分别为 , 且.(1)、求的值;(2)、若 , 求的长.
-
12、如图,这是一个平面图形,现提供四种颜色给图中的区域1、区域2、区域3、区域4、区域5、区域6共六个区域涂色,每个区域只涂一种颜色,相邻的区域不能涂相同的颜色,则共有种不同的涂色方案.
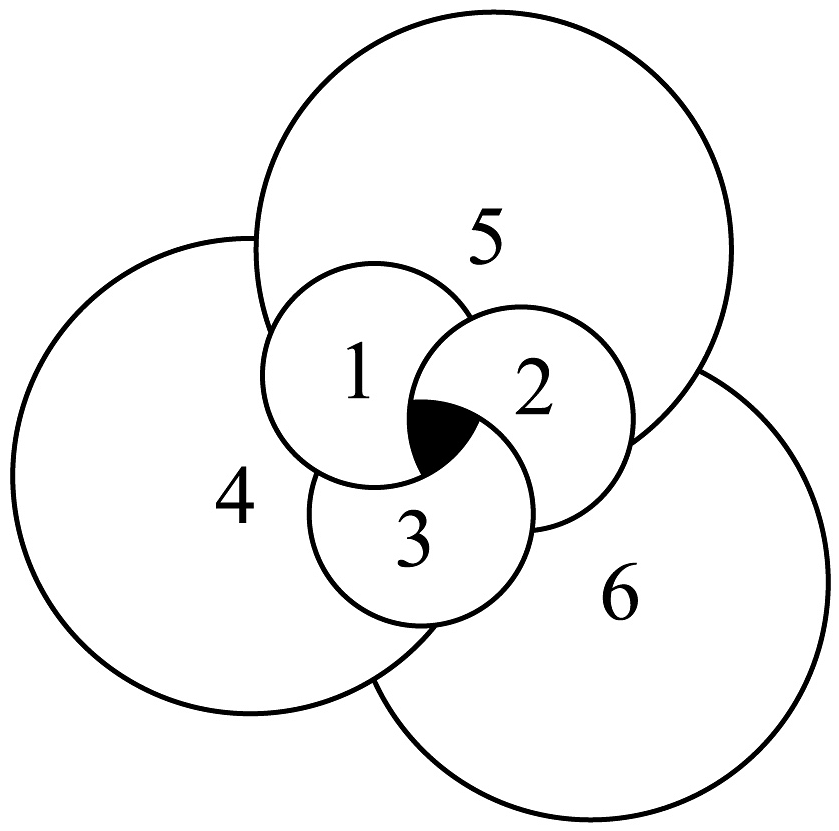
-
13、已知复数是关于的方程的一个根,则.
-
14、设正实数满足 , 则( )A、 B、 C、 D、
-
15、已知某平面图形由如图所示的四个全等的等腰拼成,其中线段的中点均为点 , 且.若将该平面图形绕着直线旋转半周围成的几何体记为 , 将该平面图形绕着直线旋转半周围成的几何体记为 , 直线直线 , 则( )
 A、的体积为 B、的表面积为 C、经过两次旋转后,点所有的运动轨迹总长为 D、经过两次旋转后,点所有的运动轨迹为两个半圆
A、的体积为 B、的表面积为 C、经过两次旋转后,点所有的运动轨迹总长为 D、经过两次旋转后,点所有的运动轨迹为两个半圆 -
16、已知函数 , 则下列结论正确的是( )A、是奇函数 B、是增函数 C、不等式的解集为 D、若函数恰有两个零点,则的取值范围为
-
17、已知函数与其导函数的部分图象如图所示.设函数 , 则( )
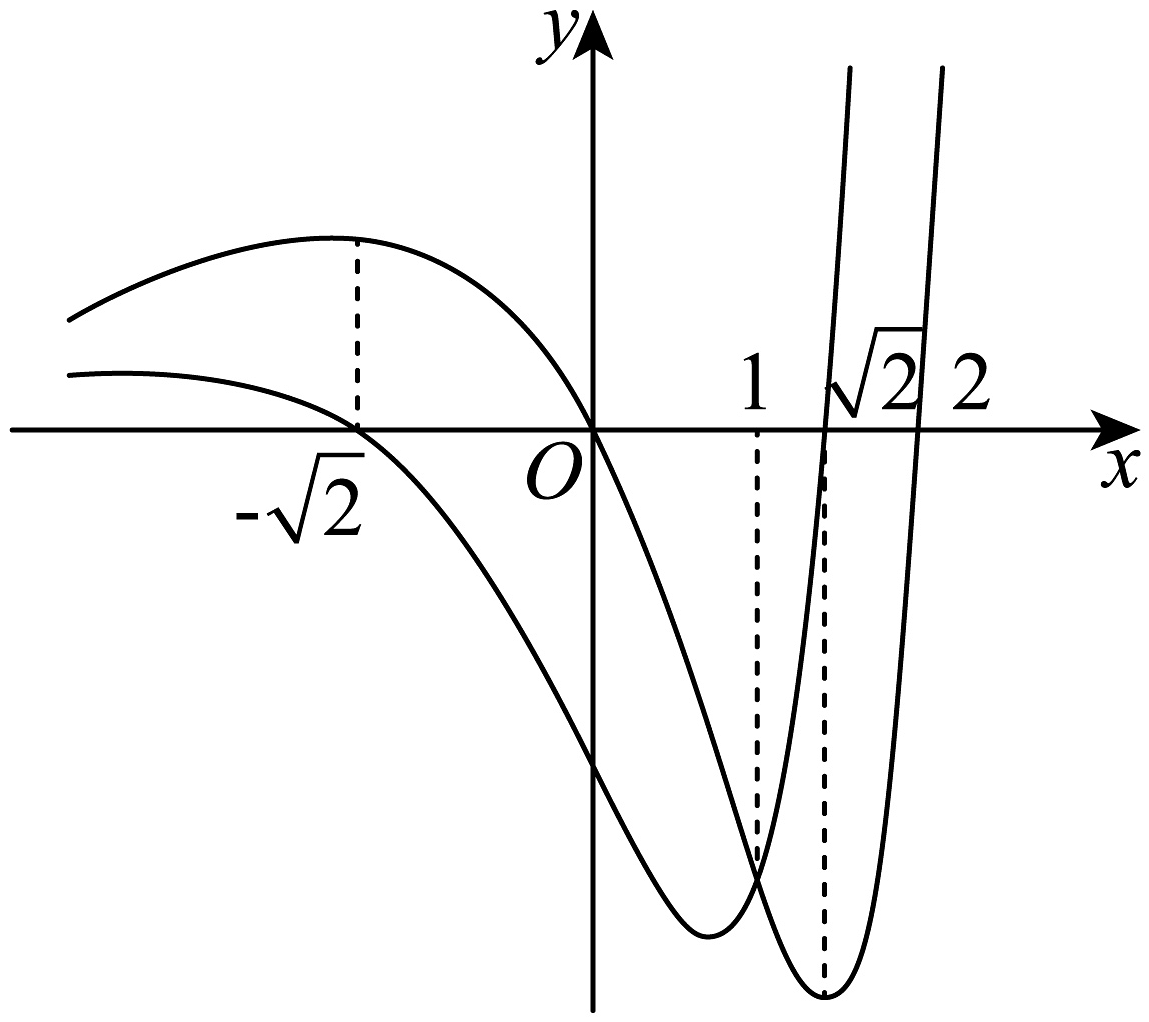 A、 B、 C、在上单调递减 D、在处取得极大值
A、 B、 C、在上单调递减 D、在处取得极大值 -
18、已知 , 则( )A、 B、 C、 D、
-
19、已知抛物线的焦点为 , 是抛物线上一点,以点为圆心的圆与直线相切于点 . 若 , 则圆的标准方程为( )A、 B、 C、 D、
-
20、定义: , 其中为向量的夹角.若 , 则( )A、8 B、16 C、 D、