相关试卷
-
1、已知随机事件是互斥事件,且 , 则下列说法错误的是( )A、 B、 C、 D、
-
2、已知平面与直线 , 则“”是“直线与平面无公共点”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
3、下列直线为函数的对称轴是( )A、 B、 C、 D、
-
4、已知 , 且 , 则实数( )A、 B、0 C、1 D、任何实数
-
5、函数的定义域是( )A、 B、 C、 D、
-
6、已知集合A={1,2},B={2,3},则AB=( )A、{2} B、{1,2,3} C、{1,3} D、{2,3}
-
7、已知函数是定义在上的偶函数,且在上单调递减,若 , 则实数的取值范围为( )A、 B、 C、 D、
-
8、已知数列 , , 记集合的元素个数为.(1)、若为1,2,4,8,12,写出集合 , 并求的值;(2)、若为1,3,a,b,且 , 求和集合;(3)、若数列项数为 , 满足 , 求证:“”的充要条件是“为等比数列”.
-
9、已知的角所对应的边为 , , .(1)、若 , 求;(2)、若 , 求;(3)、在(2)的条件下,求证:.
-
10、一种掷骰子走跳棋的游戏:棋盘上标有第站、第站、第站、、第站,共站,设棋子跳到第站的概率为 , 一枚棋子开始在第站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第站(获胜)或第站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数、、、、、).(1)、求、、 , 并根据棋子跳到第站的情况,试用和表示;(2)、求证:为等比数列;(3)、求玩该游戏获胜的概率.
-
11、已知椭圆的离心率为 , 且过点.
(1)求椭圆的标准方程.
(2)设为椭圆的左、右顶点,过的右焦点作直线交椭圆于 , 两点,分别记的面积为 , 求的最大值.
-
12、如图,在三棱柱中,AE与BD相交于点O,C在平面ABED内的射影为O,G为CF的中点.
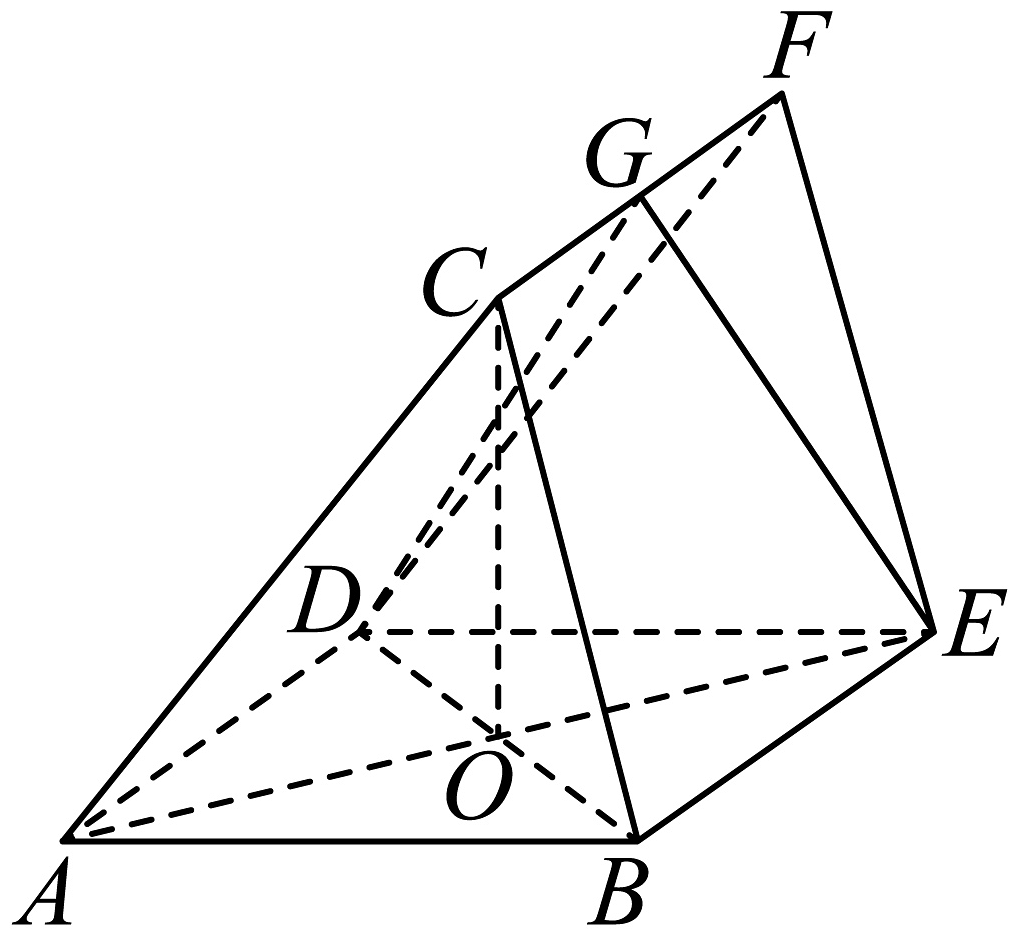 (1)、求证:平面GED;(2)、若 , 求二面角的余弦值.
(1)、求证:平面GED;(2)、若 , 求二面角的余弦值. -
13、已知函数(为自然对数的底数),若关于的方程有且仅有四个不同的解,则实数的取值范围是 .
-
14、已知函数在区间上恰有2个极大值点和1个极小值点,则的取值范围为.
-
15、已知一个圆台的上、下底面半径分别为2,4,它的侧面展开图扇环的圆心角为 , 则这个圆台的侧面积为.
-
16、已知抛物线: , 两平行直线 , 分别交于点 , , , , O为坐标原点,且 , M,N分别是 , 的中点,且 , 则( )A、恒过的焦点 B、 , 的横坐标之积为定值4 C、 , 距离的最大值为6 D、直线的斜率恒为定值
-
17、记为数列的前项和,已知则( )A、2025是数列中的项 B、数列是公比为2的等比数列 C、 D、若 , 则数列的前项和小于
-
18、已知正项等比数列的公比 , 将的前9项按照从小到大的顺序排列组成一组数据,则下列说法正确的是( )A、该组数据的分位数为 B、该组数据的中位数小于其平均数 C、若去掉 , 所得新数据的中位数与原中位数相等 D、若 , 则 , , …,的方差是 , , …,的方差的9倍
-
19、三棱锥各个顶点均在球表面上, , 外接圆的半径为 , 点在平面的射影为中点,且与平面所成的角为 , 则球的表面积为( )A、 B、 C、 D、
-
20、已知圆 , 圆 , 过动点P分别作圆圆的切线PA,PB(A,B为切点),使得 , 则动点P的轨迹方程为( )A、 B、 C、 D、