相关试卷
-
1、已知 , 且 , 则( )A、 B、 C、 D、
-
2、已知向量 , , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
3、若复数满足 , 则( )A、 B、 C、 D、
-
4、已知各项均为正数的等比数列 , 其前项和为 , 满足 ,(1)、求数列的通项公式;(2)、记为数列在区间中最大的项,求数列的前项和 .
-
5、某射击选手射击环数的分布列为
若射击不小于环为优秀,其射击一次的优秀率为 .
-
6、已知椭圆的左右焦点分别为 , , 过作直线交椭圆于 , 两点,若为线段的中点,则的面积为 .
-
7、若函数的图象过点 , 则函数的图象一定经过点.
-
8、已知直线 , , , 以下结论正确的是( )A、不论为何值时,与都互相垂直; B、当变化时,与分别经过定点和 C、不论为何值时,与都关于直线对称 D、如果与交于点M,则的最大值是
-
9、已知等边三角形内接于为线段的中点,则( )
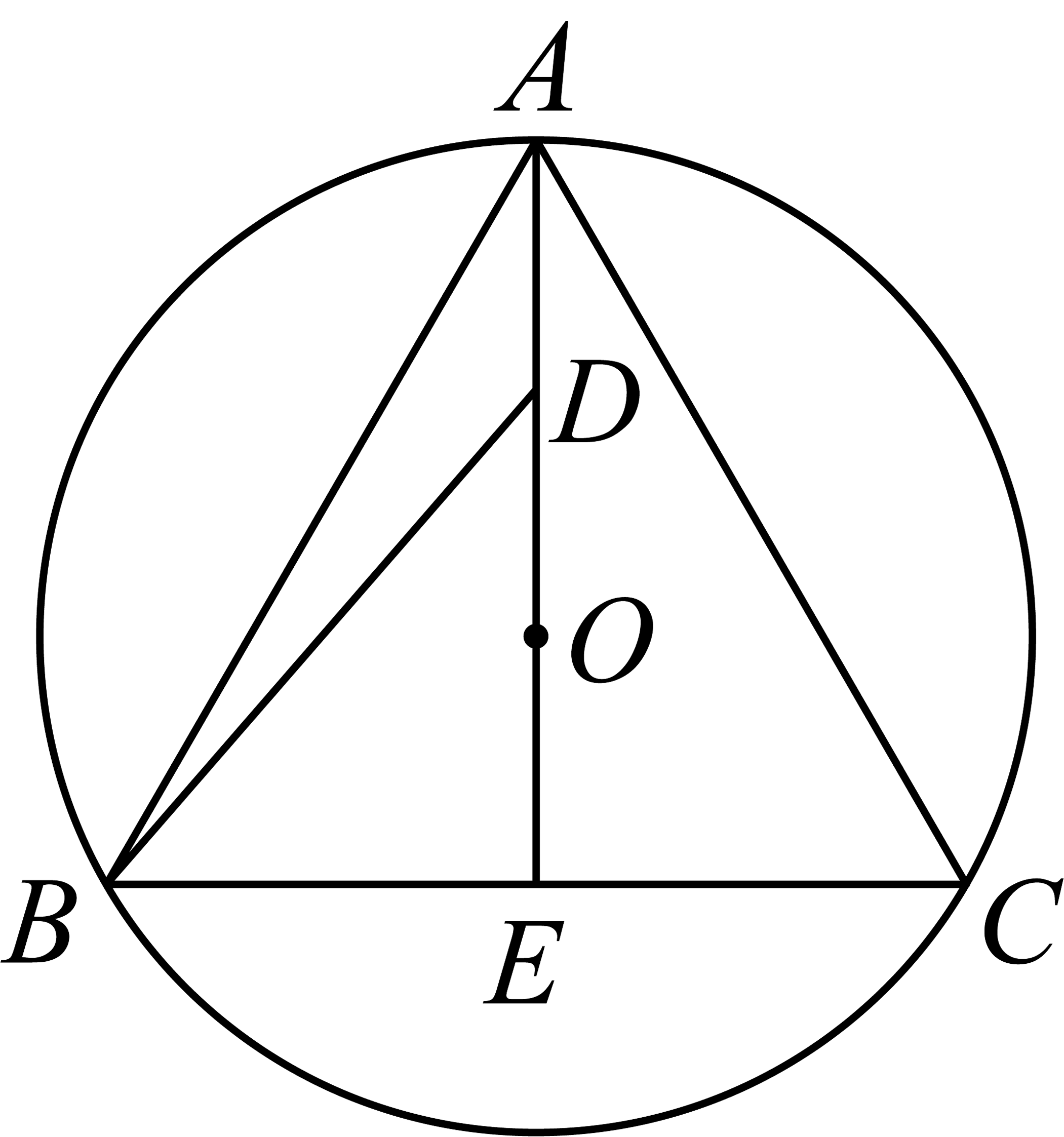 A、 B、 C、 D、
A、 B、 C、 D、 -
10、若不等式恒成立,则实数a的最大值为( )A、1 B、2 C、3 D、4
-
11、在平面直角坐标系中,某菱形的一组对边所在的直线方程分别为和 , 另一组对边所在的直线方程分别为和 , 则( )A、 B、 C、 D、
-
12、某学校于3月12日组织师生举行植树活动,购买垂柳、银杏、侧柏、海桐四种树苗共计1200棵,比例如图所示.高一、高二、高三报名参加植树活动的人数分别为600,400,200,若每种树苗均按各年级报名人数的比例进行分配,则高三年级应分得侧柏的数量为( )
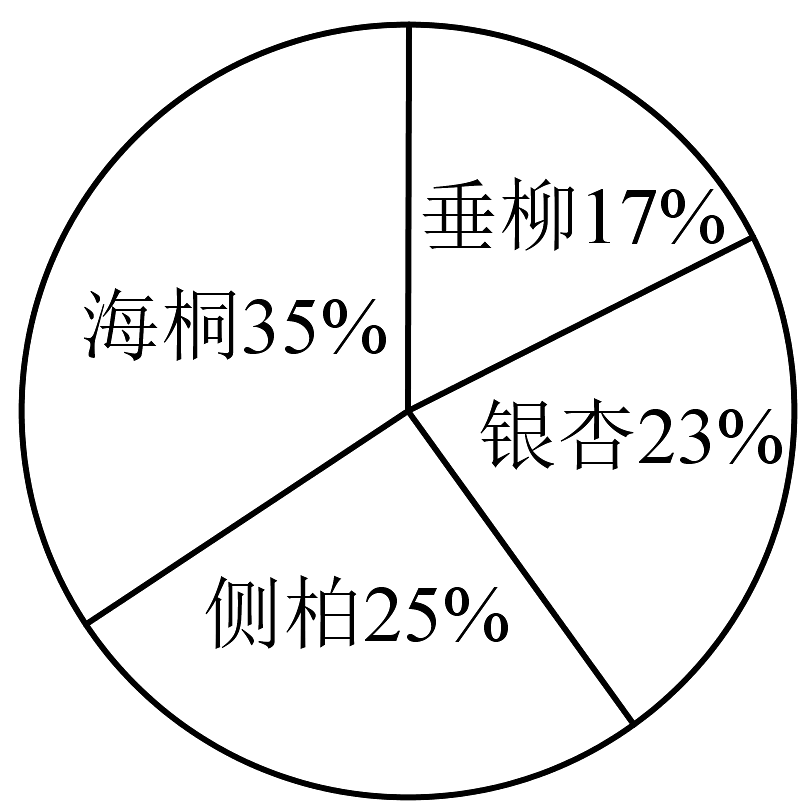 A、34 B、46 C、50 D、70
A、34 B、46 C、50 D、70 -
13、某玩具公司推出一款智能机器狗玩具,开启电源后机器狗从起点处每次向前或向后跳动1个单位,当机器狗位置距离起点处不足( , 且 , 可以进行手动设置)个单位时,每次向前跳动的概率为 , 向后跳动的概率为 , 当机器狗跳动后的位置距离起点处为个单位时,则连续向起点处跳动次,回到起点,然后从起点处重新开始跳动.(1)、若设置 , 求机器狗跳动6次后恰好回到起点的概率;(2)、若设置 , 记机器狗跳动5次后距离起点处个单位,求的分布列与数学期望;(3)、若机器狗跳动了次,求每次跳动后距离起点处都不足个单位的概率.
-
14、随着网络App的普及与发展,刷“抖音”成为了人们日常生活的一部分.某地区随机抽取了部分20~40岁的“抖音”用户,调查他们日均刷“抖音”的时间情况,所得数据统计如下表:
性别
日均刷“抖音”时间超过2小时
日均刷“抖音”时间不超过2小时
男性
48
72
女性
24
56
(1)、依据小概率值的独立性检验,能否认为日均刷“抖音”时间的长短与性别有关?(2)、现从被调查的日均刷“抖音”时间超过2小时的用户中,按照性别比例采用分层随机抽样的方法抽取3名用户参加抖音知识问答,已知男性用户、女性用户顺利完成知识问答的概率分别为 , , 每个人是否顺利完成知识问答相互独立,求在有且仅有2人顺利完成知识问答的条件下,这2人性别不同的概率.参考公式: , 其中.
参考数据:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
-
15、传统燃油汽车与新能源汽车相比,有着明显的缺点:如传统燃油汽车在行驶过程中会产生尾气排放和噪音污染,环保性能较差、能源效力较低等我国近几年着重强调可持续发展,加大在新能源项目的支持力度,积极推动新能源汽车产业迅速发展某汽车制造企业对某地区新能源汽车的销售情况进行调查,得到下面的统计表.
年份t
2019
2020
2021
2022
2023
年份代码
1
2
3
4
5
销量y(万辆)
11
13
18
21
27
(1)、统计表明销量y与年份代码x有较强的线性相关关系,求y关于x的线性同归方程,并预测该地区新能源汽车的销量最早在哪一年能突破50万辆;(2)、该企业随机调查了该地区2023年的购车情况.据调查,该地区2023年购置新能源汽车与传统燃油汽车的人数的比例大约为 . 从被调查的2023年所有车主中按分层抽样抽取12人,再从12人中随机抽取3人,记这3人中购置新能源汽车的人数为X,求X的分布列和期望.参考公式:
对于一组数据 , 其回归直线中斜率和截距的最小二乘估计公式分别为: .
-
16、甲乙两个袋子,甲袋有1白2黑3个球,乙袋有2个白球.现从两袋各取1球,交换放入甲乙两袋.如此交换两次后,甲袋中的白球个数记作X,则=.
-
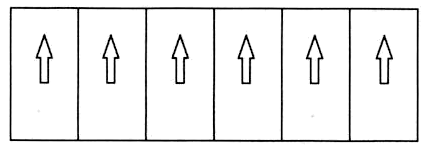
17、如图,某停车区域共有6个停车位,现有3辆白色汽车和2辆黑色汽车将停在车位上.记黑色汽车之间的白色汽车数为X,则X的数学期望为.
-
18、已知个点大致呈线性分布,其中 , 且数据的回归直线方程为 , 则的最小值为 .
-
19、100件产品中有5件次品,不放回地抽取2次,每次抽1件.已知第1次抽出的是次品,则第2次抽出正品的概率是.
-
20、已知表示中最小的数,表示中最大的数.若为的任意排列,设 , , 则( )A、排列总数为720个 B、满足的排列有80个 C、的概率为 D、的概率为