相关试卷
-
1、已知直线与平面 , 则能使的充分条件是( )A、 B、 C、 D、
-
2、已知 , 则的虚部为( )A、 B、1 C、 D、2
-
3、已知三点共线,则( )A、1 B、3 C、 D、
-
4、某市有大型超市20家、中型超市60家、小型超市120家.为掌握各类超市的营业情况,现用比例分配的分层随机抽样方法抽取一个样本容量为20的样本,则抽取中型超市的数量为( )A、12 B、6 C、4 D、2
-
5、在中,角A,B,C的对边分别是a,b,c,已知 .(1)、求角A;(2)、点M在线段上,且满足 . 若 , 求的面积.
-
6、某实验室对某二进制数码串传输进行测试,初始二进制数码串是长度为的且全部由0组成的数码串.传输过程中,每位数码以概率传输记为0,以概率传输记为1,其中 , 每位数码的传输相互独立,并设事件为“传输结果各位数字之和为偶数”的事件.(1)、当时,求;(2)、证明:对任意的正整数 , 有;(3)、在传输结果中任取一位数码,记“取到1”的事件为 , 问:是否存在最大值?若存在,求出使取到最大值的正整数;若不存在,请说明理由.
-
7、已知函数 , 其中.(1)、当时,求的单调递增区间;(2)、若恒成立,求的取值范围;(3)、试比较2.8与的大小并证明.
-
8、如图1所示,四边形满足 , 过点作 , 点在线段上,且满足 , 将沿直线翻折到的位置(图2),.
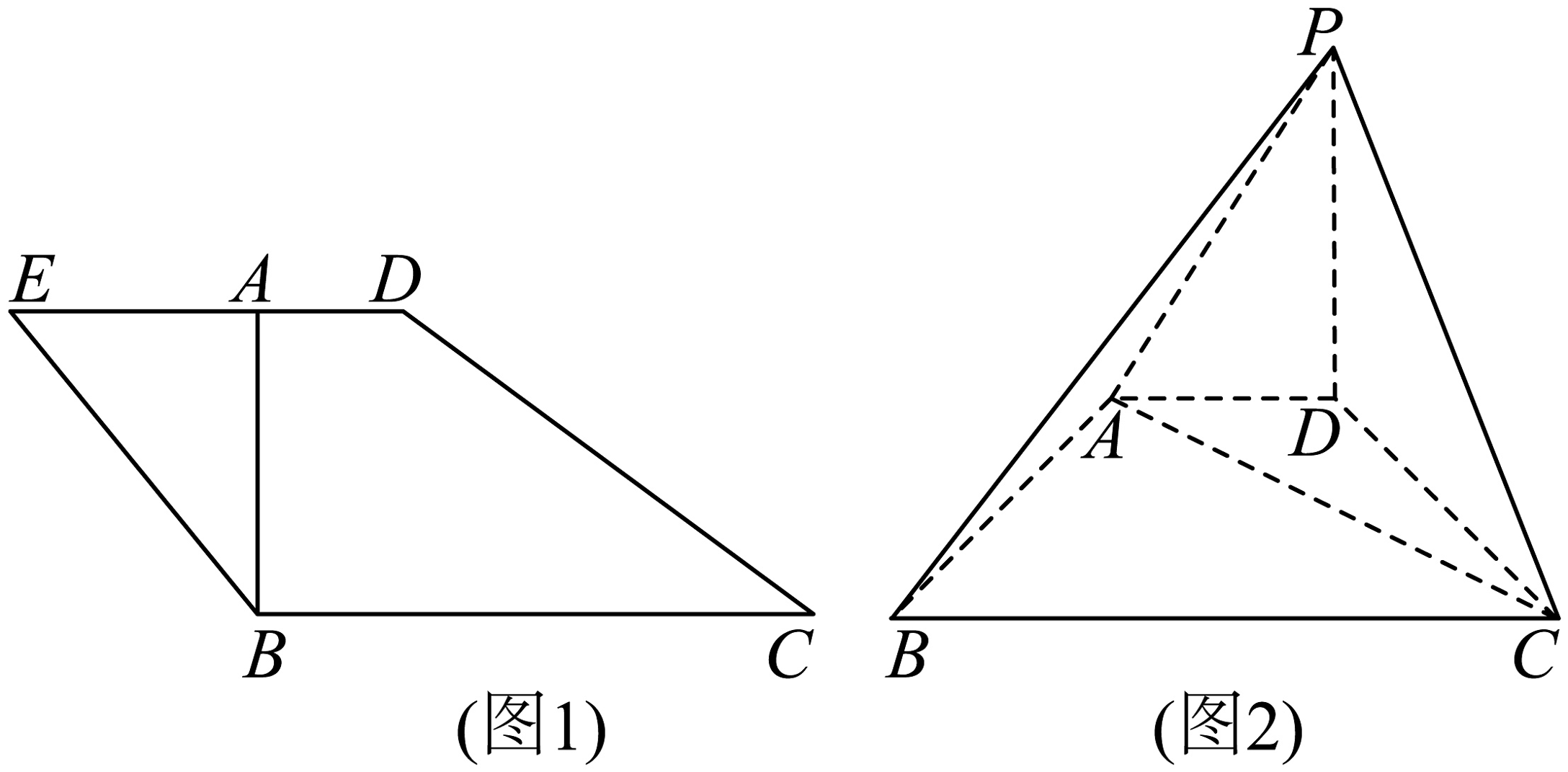 (1)、求证:;(2)、若 , 求平面与平面夹角的余弦值.
(1)、求证:;(2)、若 , 求平面与平面夹角的余弦值. -
9、已知为锐角三角形,内角A,B,C的对边分别为a,b,c,且 ,(1)、求;(2)、若 , 求面积的取值范围.
-
10、2025年3月9日,国家卫生健康委员会在第十四届全国人大三次会议民生主题记者会上表示,实施“体重管理年”3年行动.某公司为了响应国家号召,收集了总共100名30-40岁之间员工的BMI指数(BMI=体重÷身高),绘制成如下图的频率分布直方图.若该公司超重的人数占40%.(BMI≥24为超重)
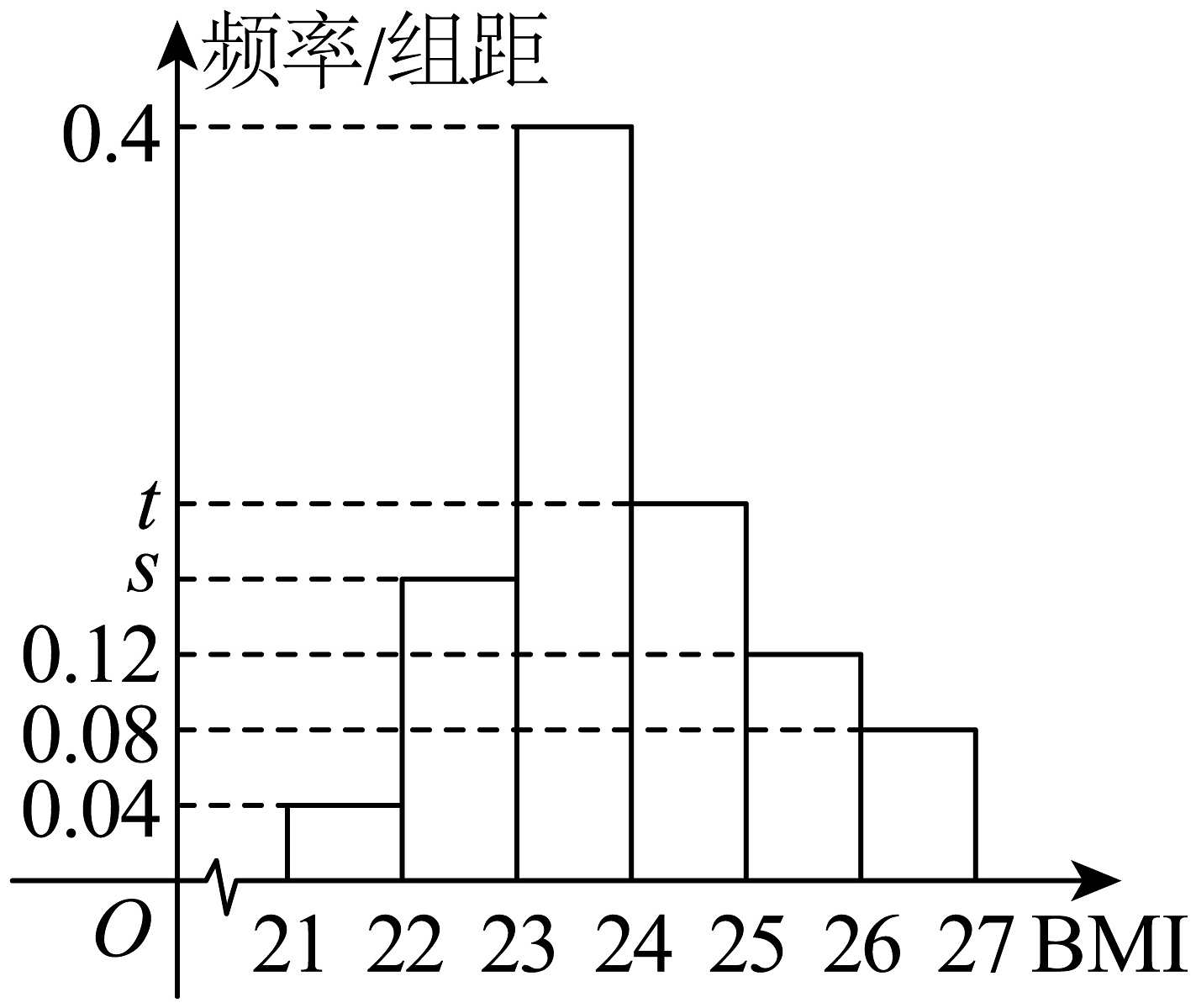 (1)、求实数s,t的值,并求该公司员工BMI指数的众数;(2)、该公司把超重的员工按性别单独做了统计,补全下面列联表,并根据小概率值的独立性检验,分析超重是否与性别有关.
(1)、求实数s,t的值,并求该公司员工BMI指数的众数;(2)、该公司把超重的员工按性别单独做了统计,补全下面列联表,并根据小概率值的独立性检验,分析超重是否与性别有关.性别
正常
超重
合计
男
20
女
20
合计
100
附:列联表参考公式: , 其中.
临界值表:
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
-
11、在正方体中, , 点E,F,G分别为 , , 的中点,点在线段上运动(不包括端点),过G,P,的平面截正方体所得的截面周长的取值范围是.
-
12、若是曲线的切线,则.
-
13、除以8的余数为.
-
14、定义在上的非常数函数满足 , 且 , 则( )A、 B、是的一条对称轴 C、 D、
-
15、下列命题正确的是( )A、若事件A,B相互独立,则 B、若 , , , 则 C、已知随机变量 , 且 , 则 D、线性相关模型中,相关系数越大,两个变量的线性相关程度越强
-
16、已知实数 , , 且 , 则( )A、 B、 C、 D、
-
17、某平面四边形中, , , , 设 , .当的面积取得最大值时,的值为( )A、 B、 C、 D、
-
18、如图所示的九宫格中共有个格点,若在其中任取3个格点,恰好能构成三角形的取法共有( )种.
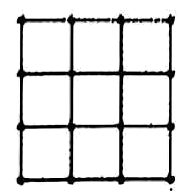 A、528 B、524 C、520 D、516
A、528 B、524 C、520 D、516 -
19、已知实数 , 正方形满足轴,且分别在 , , 的图象上,若正方形的面积为36,则( )A、 B、 C、 D、
-
20、已知向量是平面内的一组基底,则“ , 的夹角为锐角”是“”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件