相关试卷
-
1、如图,中, , , 设 , , 则( )
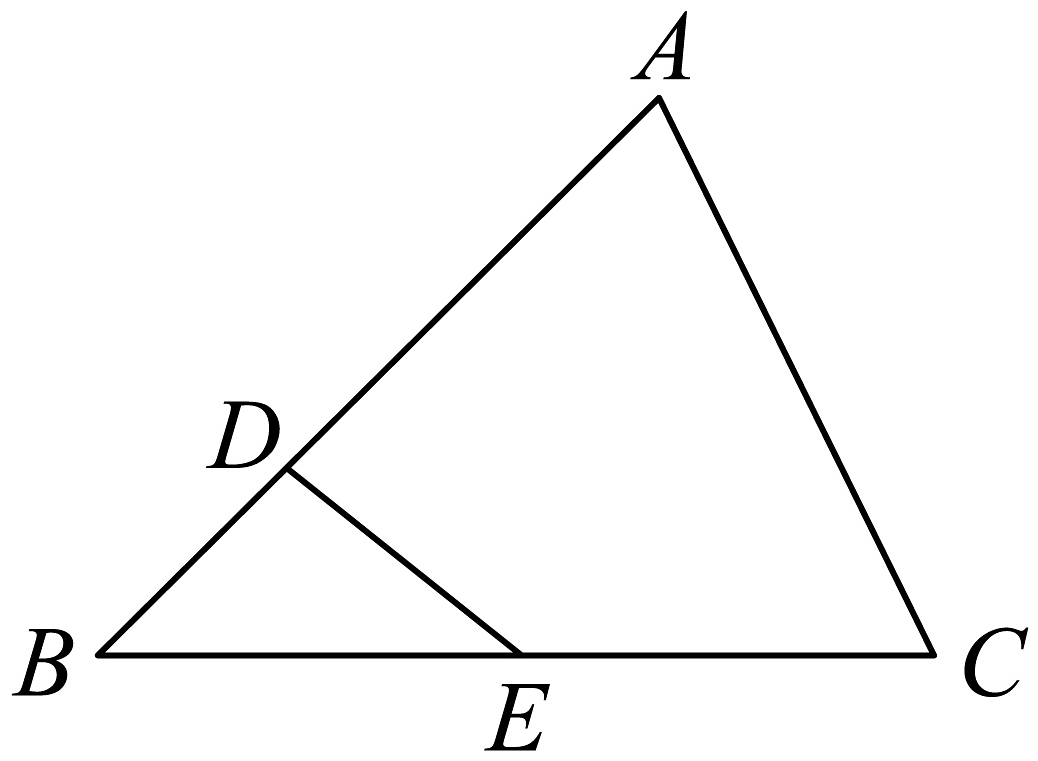 A、 B、 C、 D、
A、 B、 C、 D、 -
2、已知复数 , 则( )A、 B、 C、 D、
-
3、已知集合A={x|2≤x<4},B={x|3x-7≥8-2x},则( )A、{x|2<x<3} B、{x|2≤x≤3} C、{x|3<x<4} D、{x|3≤x<4}
-
4、已知椭圆C: , , . 椭圆C内部的一点 , 过点T作直线AT交椭圆于M,作直线BT交椭圆于N.M、N是不同的两点.(1)、若椭圆C的离心率是 , 求b的值;(2)、设的面积是 , 的面积是 , 若 , 时,求t的值;(3)、若点 , 满足且 , 则称点U在点V的左上方.求证:当时,点N在点M的左上方.
-
5、如图1,是等边三角形,为等腰直角三角形, , 将沿AC翻折到的位置,且点P不在平面ABC内)(如图2),点F在线段PB上(不含端点).
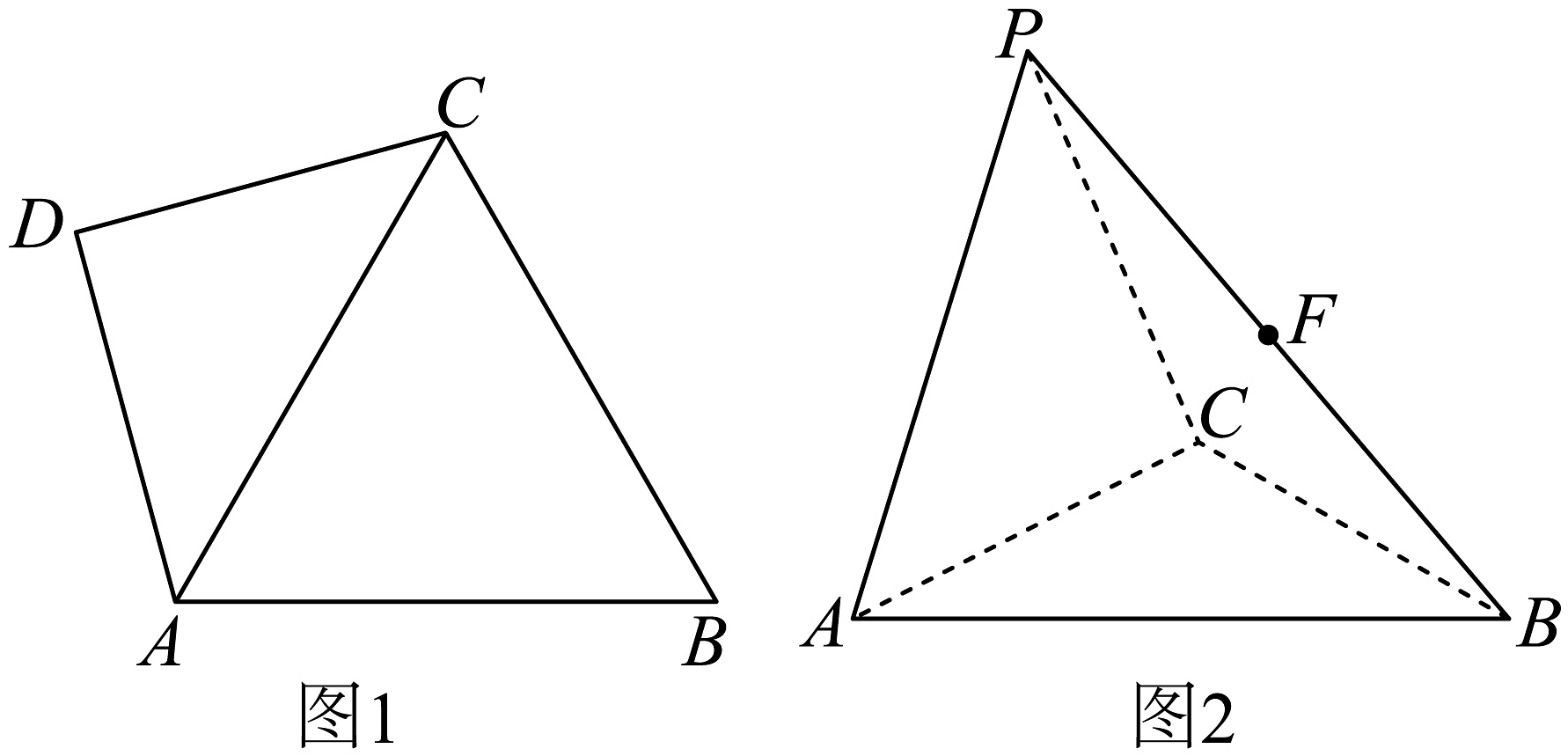 (1)、证明:;(2)、若 .
(1)、证明:;(2)、若 .(ⅰ)当点F为线段PB的中点时,求直线PB与平面ACF所成角的大小;
(ⅱ)设平面ACF与平面PBC的夹角为 , 求的取值范围.
-
6、已知函数 .(1)、讨论函数的单调性;(2)、若曲线上两点A、B处的切线都与y轴垂直,且线段与x轴有公共点,求实数a的取值范围.
-
7、体育课上,同学们进行投篮测试,规定:每位同学投篮3次,至少投中2次则通过测试,若没有通过测试,则该同学必须进行50次投篮训练.已知甲同学每次投中的概率为 , 每次是否投中相互独立.(1)、求甲同学通过测试的概率;(2)、若乙同学每次投中的概率为 , 每次是否投中相互独立.经过测试后,甲、乙两位同学需要进行投篮训练的投篮次数之和记为X.求X的分布列与数学期望 .
-
8、已知数列的前n项和为 , 且 . 数列是公比为3的等比数列,且 .(1)、求数列和数列的通项公式;(2)、令 , 求数列的前n项和 .
-
9、已知函数( , 且),若恒成立,则的最小值为 .
-
10、已知一试验田种植的某种作物一株生长果实的个数x服从正态分布 , 且 , 从试验田中随机抽取10株,果实个数在的株数记作随机变量X,且X服从二项分布,则X的方差为 .
-
11、在锐角中,则的值等于 .
-
12、设随机变量X的所有可能取为1,2,3,…,n,且 , , 现定义 , 则下列说法正确的是( )A、若 , 则 B、若 , 则随着n的增大而增大 C、若 , 则的最小值为1 D、若 , 随机变量Y的所有可能取值为1,2,…,m,且 , 则
-
13、用于加热水和食物的太阳灶应用了抛物线的光学性质:一束平行于抛物线对称轴的光线,经过抛物面(抛物线绕它的对称轴旋转所得到的曲面叫抛物面)反射后,集中于它的焦点.若抛物线C:的焦点为F,O为坐标原点,一条平行于x轴的光线从点M射入,经过C上的点反射,再经过C上另—点反射后,沿直线射出,则( )A、C的准线方程为 B、 C、若点 , 则 D、设直线与C的准线的交点为 , 则点在直线上
-
14、已知函数 , 则( )A、为偶函数 B、 C、无零点 D、在上单调递减
-
15、已知 , 均为锐角,且 , 则( )A、 B、 C、 D、
-
16、如图,在正方体中,分别为所在棱的中点,为下底面的中心,则下列结论中错误的是( )
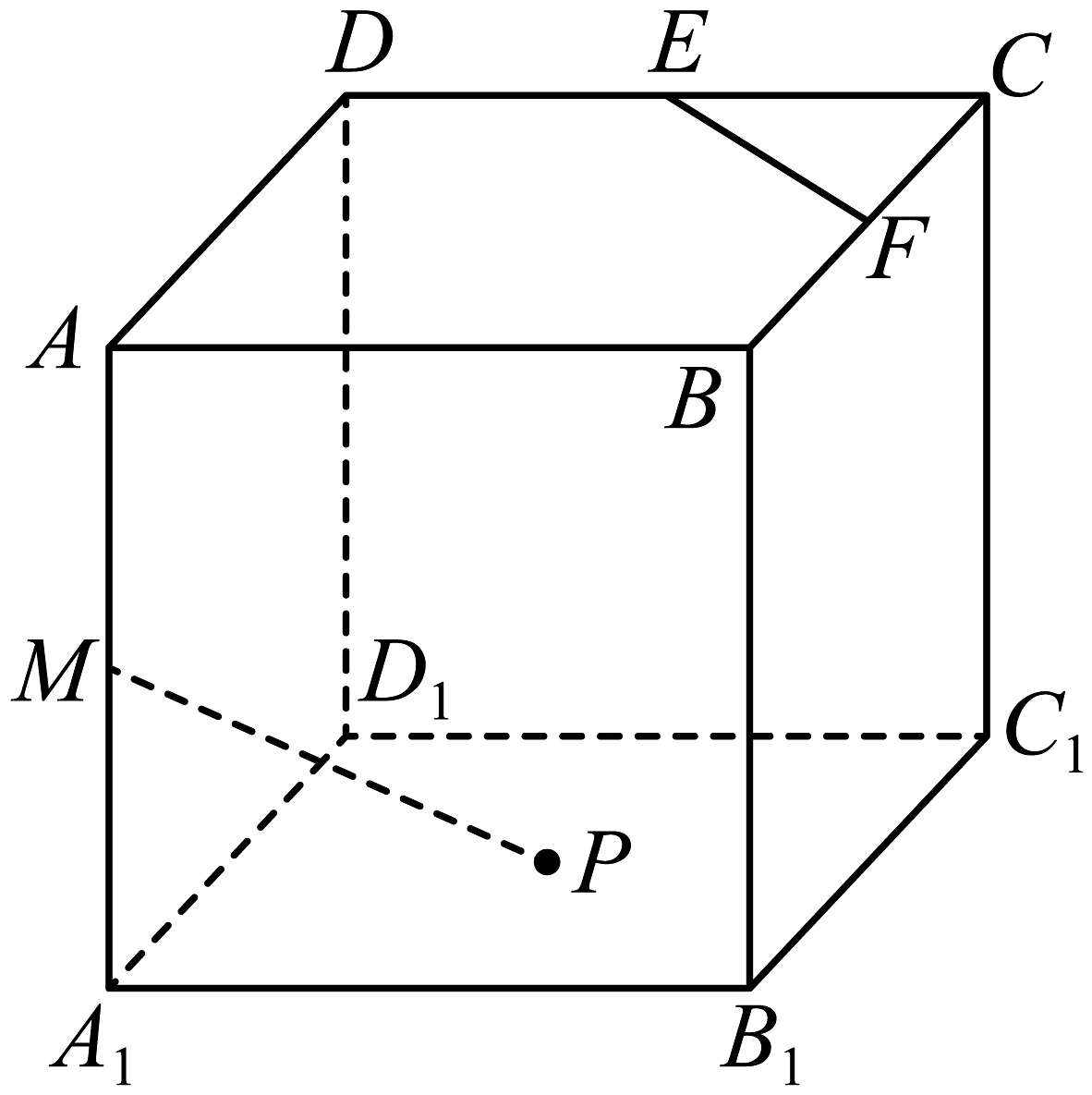 A、平面平面 B、 C、 D、平面
A、平面平面 B、 C、 D、平面 -
17、2024年惠州马拉松赛事期间,组委会需从甲、乙、丙、丁4位志愿者中选3位安排到物资分发、路线指引、医疗协助三个不同服务点,每个服务点1人.已知甲不能安排在物资分发服务点,则不同的安排方法共有( )A、9种 B、12种 C、15种 D、18种
-
18、已知 , 则( )A、 B、 C、 D、
-
19、已知单位向量满足 , 则与的夹角为( )A、 B、 C、 D、
-
20、已知复数满足 , 则( )A、 B、 C、 D、