相关试卷
-
1、在空间中,点为定点,设集合 , 则以下说法正确的是( ).
①若在上的数量投影为 , 则线段在运动过程中所形成的几何体体积为;
②对于任意的以及任意的正实数 , 设 , 若 , 则.
A、①是真命题,②是真命题 B、①是真命题,②是假命题 C、①是假命题,②是真命题 D、①是假命题,②是假命题 -
2、如图,在正三棱柱中,点D是BC的中点, .
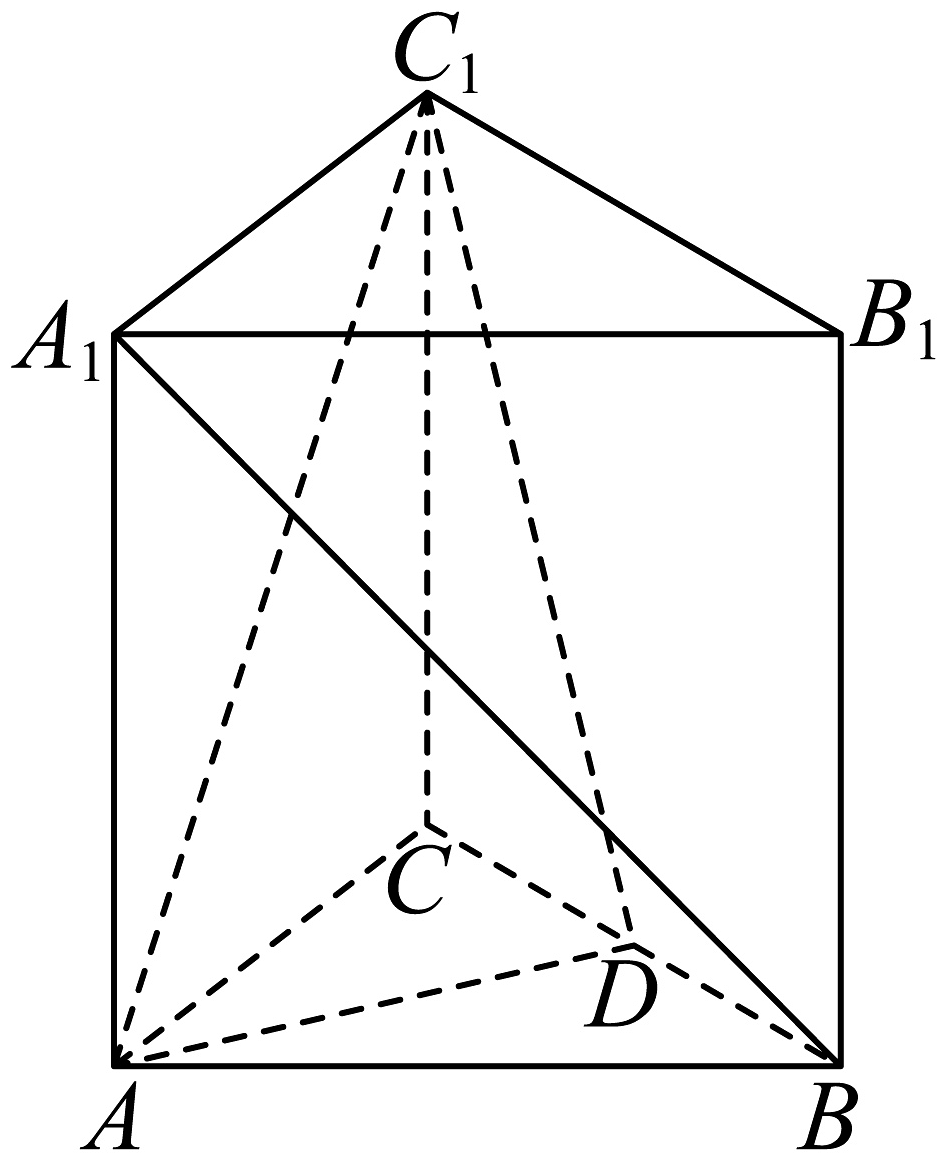 (1)、求证:平面;(2)、求证:平面平面;(3)、求直线到平面的距离.
(1)、求证:平面;(2)、求证:平面平面;(3)、求直线到平面的距离. -
3、在中,角、、所对的边分别为、、 , 且 , , ,(1)、求角的大小;(2)、若 , 的面积为 , 求的周长.(3)、若三角形为锐角三角形,且 , 求周长的取值范围.
-
4、设 , 是非零复数, , 分别是 , 的共轭复数,则下列结论中正确的是( )A、 B、 C、 D、若 , 则的最大值为
-
5、在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,已知 , 则的取值范围是( )A、 B、 C、 D、
-
6、在平行四边形中,已知 , (如图1),将沿BD折起到的位置(如图2),使得平面平面 , 则直线SB与直线CD所成角为( )
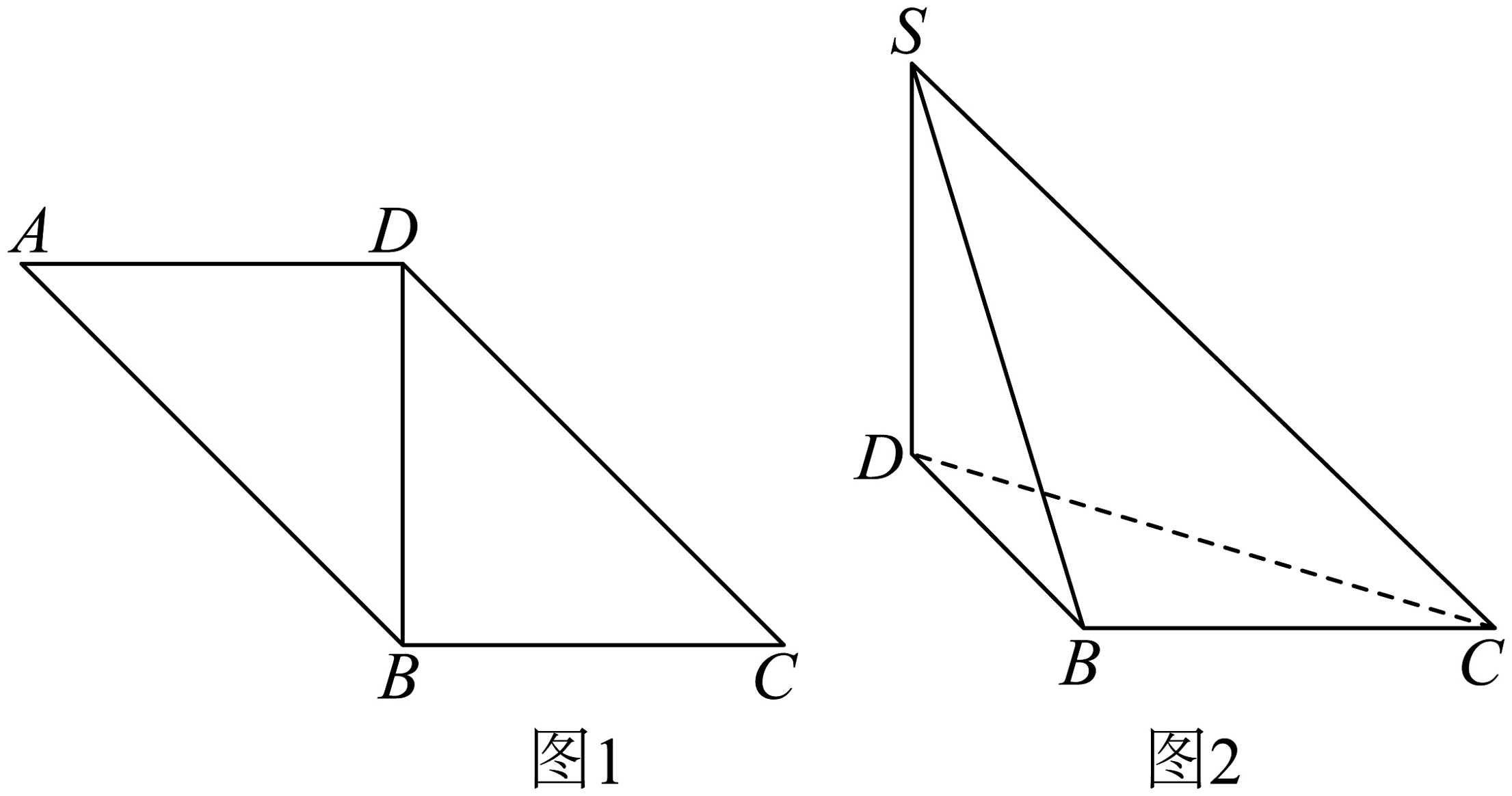 A、30° B、60° C、90° D、120°
A、30° B、60° C、90° D、120° -
7、已知向量和满足 , , 向量在向量上的投影向量为 , 则( )A、3 B、 C、4 D、12
-
8、若的方差为3,则的方差为( )A、3 B、6 C、9 D、12
-
9、下列各组向量中,可以作为基底的是( ).A、 , B、 , C、 , D、 ,
-
10、已知集合 , 则图中阴影部分所表示的集合为( )
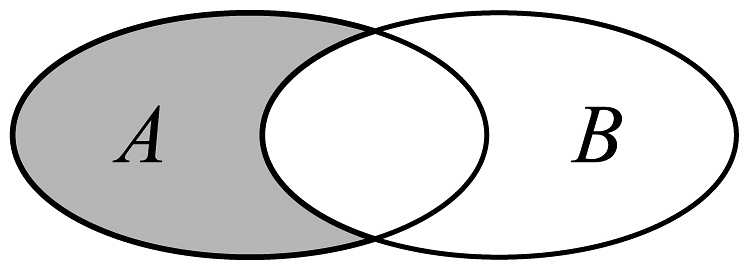 A、 B、 C、 D、
A、 B、 C、 D、 -
11、记为等差数列的前n项和.若 , 则 .
-
12、若斜率为1的直线与曲线和圆都相切,则实数的值为( )A、 B、0 C、2 D、0或2
-
13、AI的快速发展在某些方面引发了人们对自己所在行业前景的焦虑,某心理辅导机构为了了解人们对于未来行业前景的焦虑是否与性别有关,对某社区居民进行了一次抽样调查,分别抽取男性和女性各50人作为样本,得到如下数据.
焦虑
不焦虑
合计
男性
10
女性
20
合计
(1)、根据已知条件,填写上面列联表,并根据小概率值为的独立性检验,能否认为该社区居民对行业前景的焦虑与性别有关?(2)、现从该样本焦虑的居民中,采用分层随机抽样的方法随机抽取6人进行问卷调查,再从这6人中随机抽取3人进行心理辅导,设抽取的3人中男性的人数为 , 求的分布列和数学期望.附:为样本容量.
-
14、已知 , 若为纯虚数,则.
-
15、记的内角的对边分别为 , 已知且均为整数.(1)、求的值;(2)、设的中点为 , 求的余弦值.
-
16、“你好!我是DeepSeek,很高兴见到你!我可以帮你写代码,读文件,写作各种创意内容,请把你的任务交给我吧”,DeepSeek从横空出世到与我们日常相伴,成为我们解决问题的“好参谋,好助手”,AI大模型正在改变着我们的工作和生活的方式.为了解不同学历人群对DeepSeek的使用情况,随机调查了200人,得到如下数据:
单位:人
学历
使用情况
合计
经常使用
不经常使用
本科及以上
65
35
100
本科以下
50
50
100
合计
115
85
200
(1)、依据小概率值的独立性检验,能否认为DeepSeek的使用情况与学历有关?(2)、某公司组织“AI模型”知识应用竞赛,将参与活动的员工分成了、、三组进行,其规则:竞赛发起权在哪一组,该组都可向另外两组发起竞赛,则下一次竞赛发起权移交给被挑战的那组.首先由组先发起竞赛,组挑战组、组的概率均为 , 若组挑战组,则下次竞赛发起权在组,若组挑战组,则下次竞赛发起权在组;若竞赛发起权在组,则挑战组、组的概率分别为和;若竞赛发起权在组,则挑战组、组的概率分别为和.①经过3次挑战赛后,求竞赛发起权在组的次数的分布列与数学期望;
②定义:已知数列 , 若对于任意给定的正数(不论它多么小),总存在正整数 , 使得当时,(是一个确定的实数),则称数列为“聚点数列”,称为数列的聚点.经过次竞赛后,竞赛发起权在组的概率为 , 证明数列为“聚点数列”,并求出聚点的值.
附: , .
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
17、已知抛物线的焦点为 , 过点的直线交抛物线于、两点,过点的直线交抛物线于、两点,且.
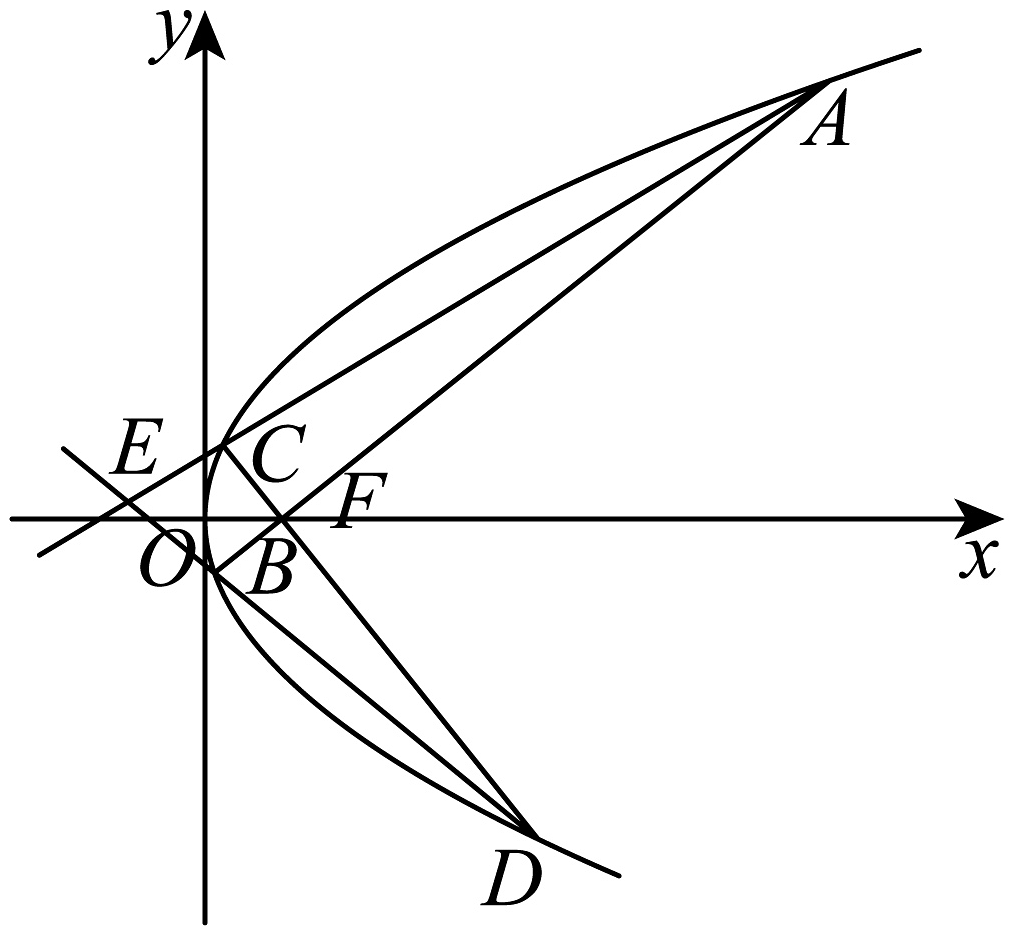 (1)、求证:为定值,并求出该定值;(2)、如图,点、在轴的同侧, , 直线与直线的交点为 , 记 , 的面积分别为 , , 求的取值范围.
(1)、求证:为定值,并求出该定值;(2)、如图,点、在轴的同侧, , 直线与直线的交点为 , 记 , 的面积分别为 , , 求的取值范围. -
18、已知函数.(1)、若曲线在处的切线与垂直,求实数的值;(2)、当 , 在区间上不单调,求实数的取值范围;(3)、若 , 对任意且 , 不等式成立,求的最小值.
-
19、在平面四边形中, , , 将沿翻折至 , 其中为动点.
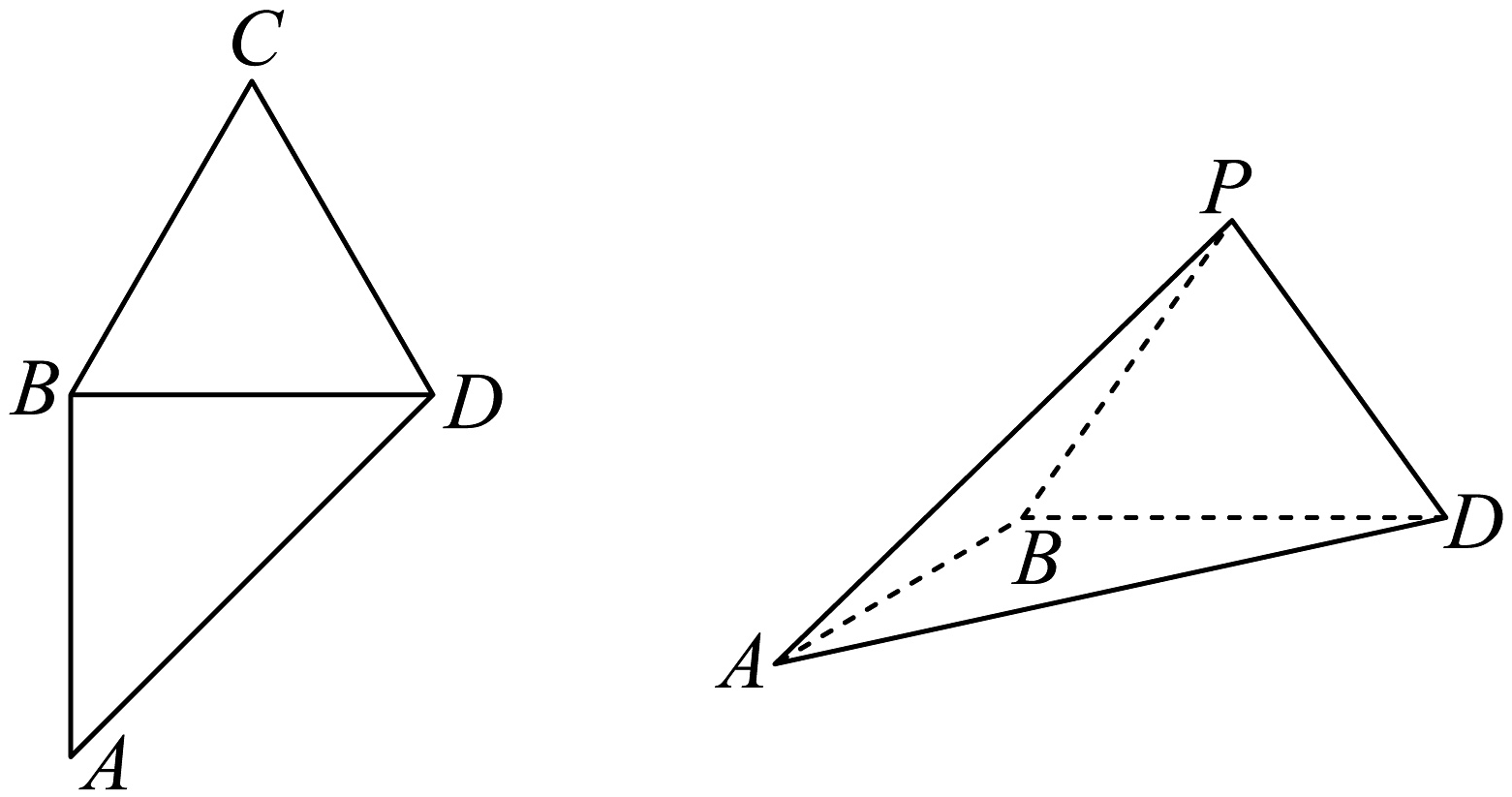 (1)、若 , 证明:平面;(2)、求直线与平面所成角的正弦值的最大值.
(1)、若 , 证明:平面;(2)、求直线与平面所成角的正弦值的最大值. -
20、已知数列的首项 , 的前项和为且满足.(1)、证明:数列是等差数列;(2)、若 , 求数列的前项和.