相关试卷
-
1、已知a,b为实数,则“”是“且”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
2、一个不透明盒子中装有4个红球和3个白球,这些球除颜色外无其它差别.从袋子中随机摸出一个球,则摸到红球的概率是( )A、 B、 C、 D、
-
3、复数 , 则的实部为( )A、3 B、 C、1 D、2
-
4、甲乙两名选手参加某球类比赛,比赛采用积分制:赛满奇数局,赢1局得2分,输者不得分,积分多者胜.已知甲选手每局比赛获胜的概率为 , 每局比赛的结果相互独立.(1)、若两人共进行了3局比赛,且 , 求甲最终获胜的概率及甲得分的方差;(2)、若两人共进行了局比赛,甲最终获胜的概率为 , 证明: , 并说明其统计意义.
-
5、已知函数 .(1)、讨论的单调性;(2)、若 , 求实数的取值范围;(3)、当时,若关于的方程有两个实根和 , 求证: .
-
6、已知各项均为正数的数列的前项和为 , , .(1)、若为等比数列,求和数列的前项和;(2)、若 , 求数列的通项公式.
-
7、如图,在四棱锥中,底面ABCD为矩形,平面ABCD, , , E为PD的中点.
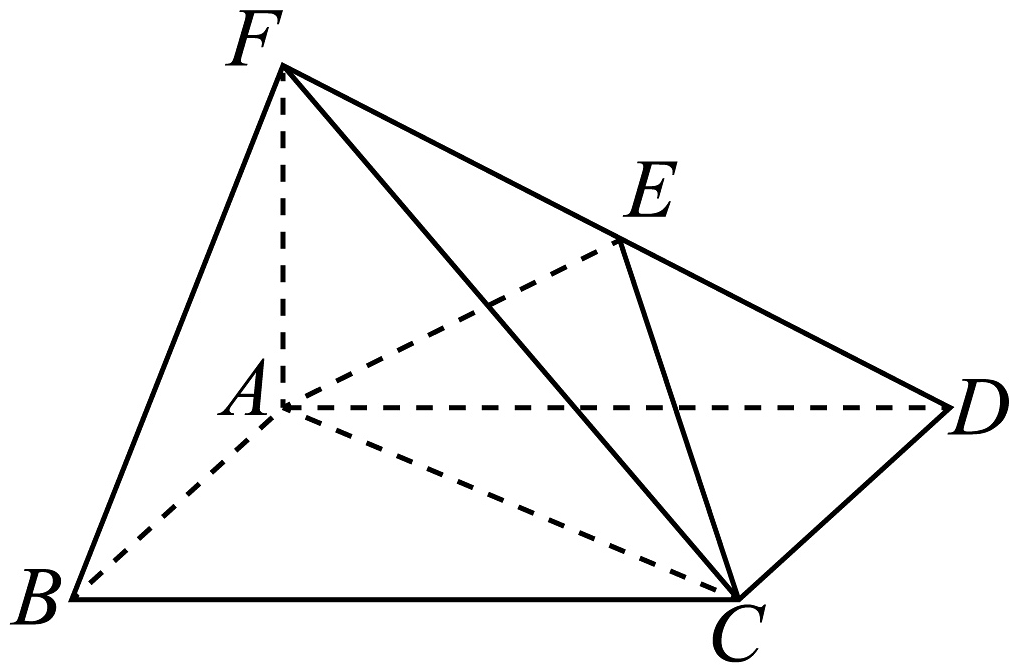 (1)、证明:平面;(2)、求二面角的余弦值.
(1)、证明:平面;(2)、求二面角的余弦值. -
8、一个袋子中有大小相同的6个小球,分别标记着1,2,2,3,4,5,现从中随机摸出3个小球.记摸到的小球上的数字的最小值为 .(1)、求;(2)、求的分布列和数学期望.
-
9、在棱长为1个单位的正四面体ABCD上,一个质点在随机外力的作用下从顶点出发,每隔1秒等可能地沿着棱移动1个单位,移动的方向是随机的.设经过秒()后,质点位于平面BCD的概率为 , 则 , .
-
10、已知函数 , 则在处的切线方程为 .
-
11、展开式中的系数为 .
-
12、已知为数列的前项和, , 则( )A、为定值 B、数列是递增数列 C、 D、数列是递增数列
-
13、已知函数 , 则( )A、可能没有零点 B、有两个极值点 C、 , 在有最大值 D、 , 在单调递增
-
14、设随机变量 , 随机变量 , 则( )A、 B、 C、 D、
-
15、今年某企业投产高新设备,合格品全部销售完毕,预设第个月将实现销量倍增的目标.已知每月产量在前一个月的基础上提高 , 第个月产品合格率为 , 前个月合格率每月增加 , 之后合格率保持不变.则的值为( )(且 , 参考数据: , )A、 B、 C、 D、
-
16、某运动质点位移与时间之间的关系为 , 则该质点的最大瞬时速度是( )A、 B、1 C、 D、2
-
17、为了检测某种药物对预防疾病的效果,进行了小动物试验,得到如下列联表:
药物
疾病
合计
未患病
患病
服用
18
7
25
未服用
12
8
20
合计
30
15
45
已知 , . 根据小概率值的独立性检验,则下列结论正确的是( )
A、药物对预防疾病有效果 B、药物对预防疾病有效果,这个结论犯错误的概率不超过0.05 C、药物对预防疾病无效果 D、药物对预防疾病无效果,这个结论犯错误的概率不超过0.05 -
18、已知等差数列的前项和为 , , 则( )A、 B、 C、 D、
-
19、某种产品的加工需要经过道工序,如果其中的、两道工序必须相邻,则加工顺序共有( )A、种 B、种 C、种 D、种
-
20、如图,中, , , 设 , , 则( )
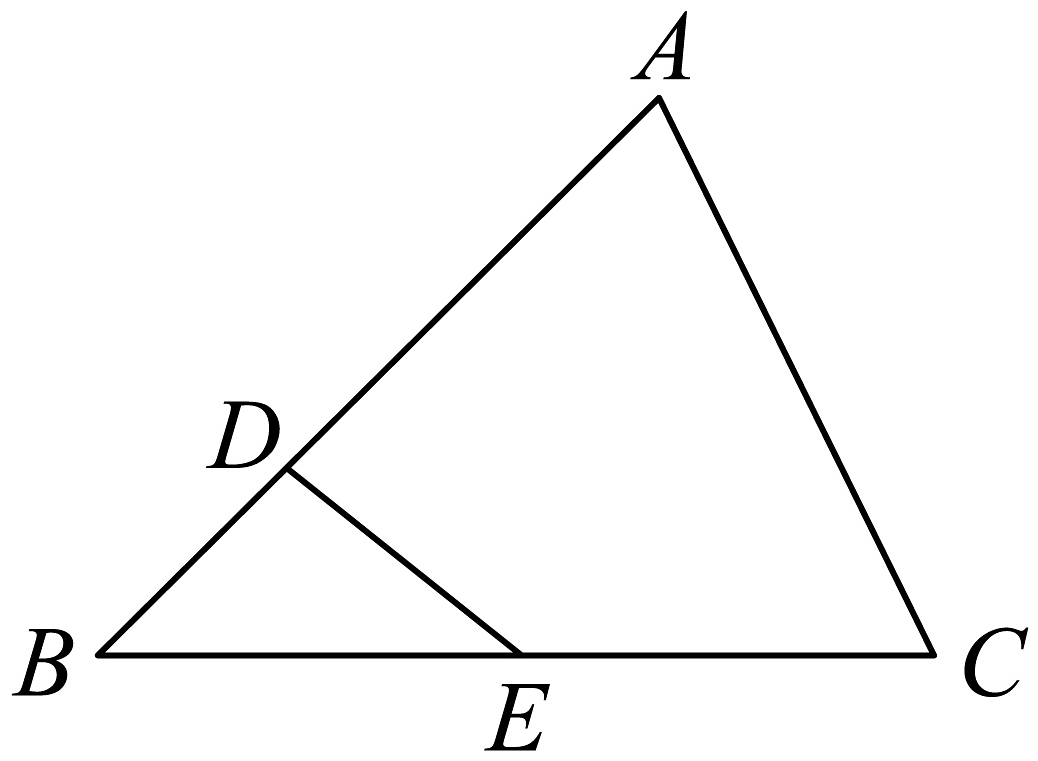 A、 B、 C、 D、
A、 B、 C、 D、