相关试卷
-
1、如图,六面体中,四边形为菱形, , , , 且平面平面.
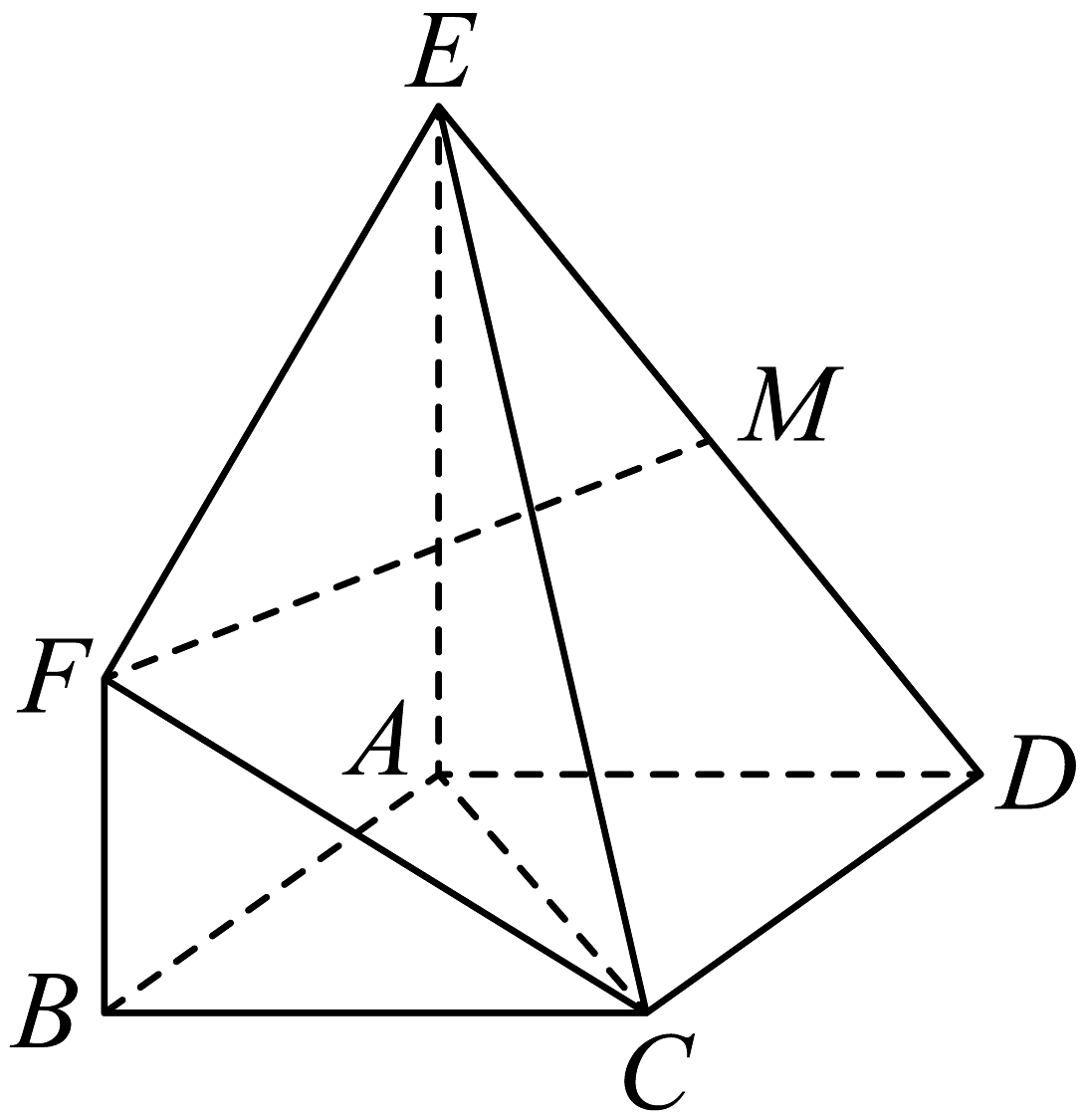 (1)、点M是棱的中点,求证:平面;(2)、求证:平面;(3)、若 , 求平面与平面夹角的余弦值.
(1)、点M是棱的中点,求证:平面;(2)、求证:平面;(3)、若 , 求平面与平面夹角的余弦值. -
2、从某学校的600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 , 第二组 , …,第八组 , 图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
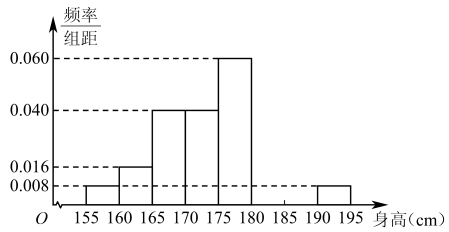 (1)、求第六组,第七组的频率;(2)、估计该校的600男生的身高的平均数和第75百分位数(精确到0.1),(3)、若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 , , 事件 , 求.
(1)、求第六组,第七组的频率;(2)、估计该校的600男生的身高的平均数和第75百分位数(精确到0.1),(3)、若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 , , 事件 , 求. -
3、记的内角A,B,C的对边分别为a,b,c,已知 , .(1)、若此三角形有两个解,求b的取值范围;(2)、若 , 求;(3)、若 , 求的面积.
-
4、已知向量 , 满足 , , 且与的夹角为.(1)、分别求与的值;(2)、若 , 求的值.
-
5、在锐角中,角A,B,C所对的边分别为a,b,c,面积为S,且 , 则的取值范围是.
-
6、某公园设置了一些石凳供大家休息,每张石凳是由正方体石料截去八个一样的四面体得到的,如图所示.如果原正方体石料棱长是 , 那么一张石凳的表面积是.

-
7、已知 , 为两个不共线的向量, , , 则(用 , 表示)
-
8、如图,在棱长为2的正方体中,点M,P分别为线段 , 上的动点,则下列说法中正确的是( )
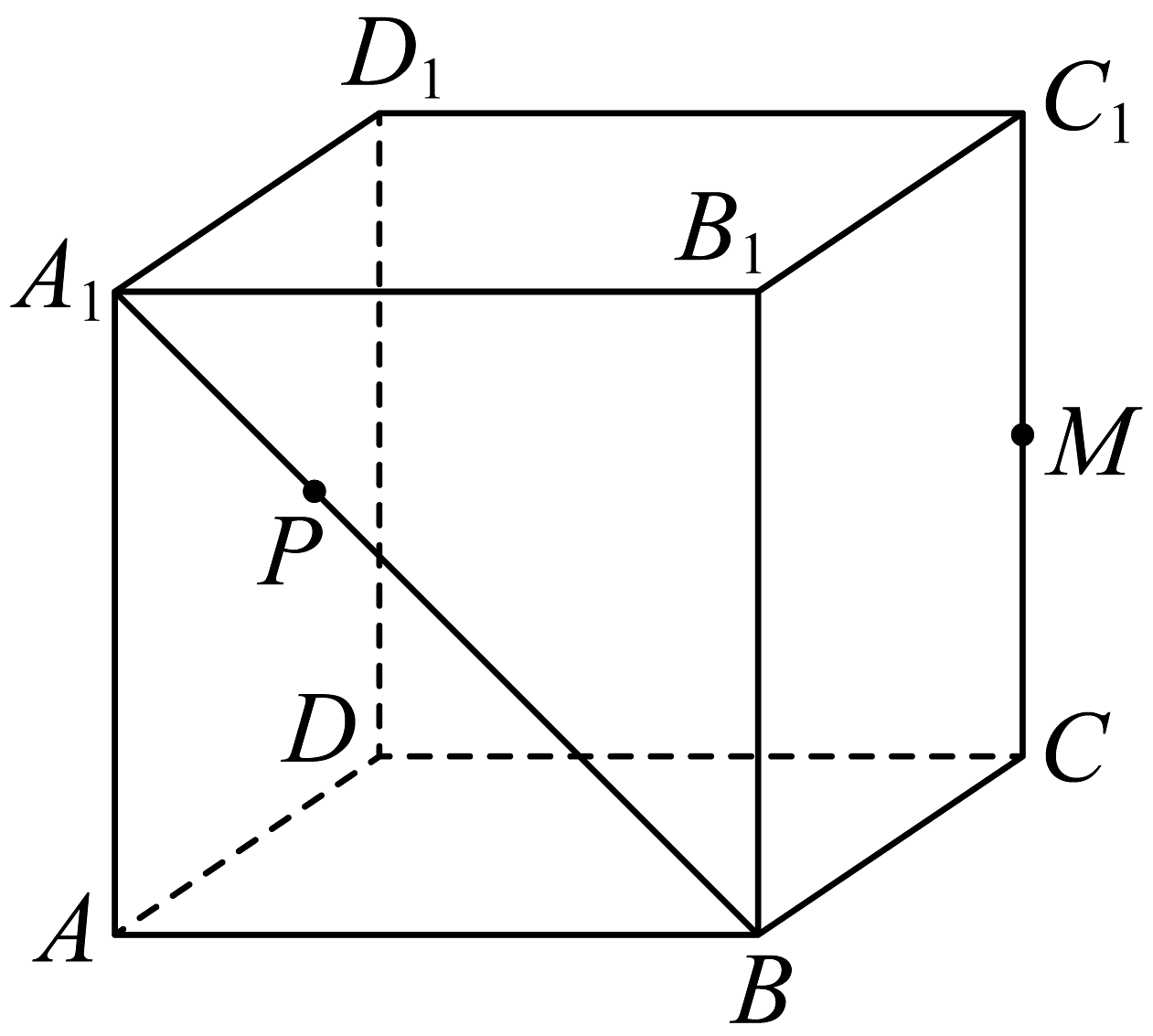 A、当M,P分别为线段 , 中点时, , B、取得最小值 C、当四面体的四个顶点在同一球面上时,若 , 则球体积为 D、对任意点M,平面平面
A、当M,P分别为线段 , 中点时, , B、取得最小值 C、当四面体的四个顶点在同一球面上时,若 , 则球体积为 D、对任意点M,平面平面 -
9、射击场,甲乙两人独立射击同一个靶子,击中靶子的概率分别为 , .记事件A为“两人都击中”,事件B为“至少1人击中”,事件C为“无人击中”,事件D为“至多1人击中”则下列说法正确的是( )A、事件A与C是互斥事件 B、事件B与D是对立事件 C、事件C与D相互独立 D、
-
10、已知复数 , 则( )A、 B、 C、为实数 D、在复平面内对应的点位于第三象限
-
11、在正方体中是棱的中点,是四边形内一点(包含边),则直线与平面所成角的正弦值取值范围是( )A、 B、 C、 D、
-
12、甲、乙两人独立地攻克一道难题,已知两人能攻克的概率分别是 , , 则下列概率计算正确的是( )A、该题被攻克的概率为 B、该题未被攻克的概率为 C、该题至少被一人攻克的概率为 D、该题至多被一人攻克的概率为
-
13、已知向量 , , 那么向量在向量上的投影向量为( )A、1 B、 C、 D、
-
14、某学生为测量宁波天封塔的高度,如图,选取了与天封塔底部D在同一水平面上的A,B两点,测得 , 在A,B两点观察塔顶C点,仰角分别为和 , 且 , 则宁波天封塔的高度是( )
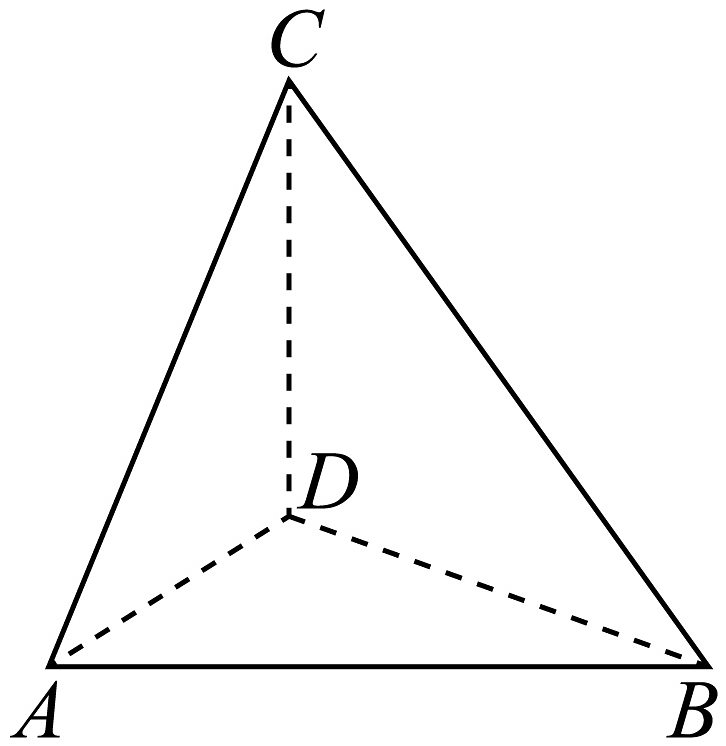 A、50m B、 C、 D、
A、50m B、 C、 D、 -
15、已知直线 , m,n与平面 , , 下列命题正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , 则
-
16、若△ABC中,角A,B,C的对边分别为a,b,c.若a2 +b2-c2=ab,则C=A、 B、 C、 D、
-
17、某高中三个年级共有学生1200人,其中高一500人,高二400人,高三300人,该校为了解学生睡眠情况,准备从全校学生中抽取60人进行访谈,若采取按比例分配的分层抽样,且按年级来分层,则高一年级应抽取的人数是( )A、20 B、25 C、30 D、35
-
18、已知向量 , 满足 , ,(1)、求与的夹角;(2)、若 , 求的值;(3)、若为锐角,求的取值范围.
-
19、已知的内角 , , 的对边分别为 , , , 则下列说法正确的是( )A、若 , 则为锐角三角形 B、若 , 则为等腰三角形 C、是的充要条件 D、若 , , , 则有两解
-
20、设函数 , , , 的极大值点为.(1)、求;(2)、若曲线 , 上分别存在两点 , 使得四边形为边平行于坐标轴的矩形,求的取值范围.