相关试卷
-
1、如图,A,B两点在河的两岸,在B同侧的河岸边选取点C,测得 , , , 则A,B两点间的距离为m.
-
2、样本中共有5个数据值,其中前四个值分别为1,2,3,5,第五个值丢失,若该样本的平均数为2,则样本方差为 .
-
3、若复数满足 , 则的最大值为 .
-
4、记 , , 则( )A、的取值范围为 B、若 , 则 C、的最小值为 D、若 , 则b的最大值为1
-
5、某中学冬季田径运动会中,高一男子跳高比赛组的前七名成绩(单位:厘米)为:145,155,132,135,140,130,136,则( )A、该组数据的极差是35 B、该组数据的中位数是136 C、该组数据的40%分位数是135 D、该组数据的平均数为139
-
6、已知中,点 , , 分别为 , , 的中点,则( )A、 B、 C、点A的坐标为 D、的面积为4
-
7、已知圆锥的侧面面积为 , 母线长为 , 则圆锥的外接球的表面积为( )A、 B、 C、 D、
-
8、若将函数的图象向左或右平移个单位,所得的图象与的图象关于y轴对称,则的最小正值是( )A、 B、 C、 D、
-
9、已知的三条边长分别为a,b,c,且 , 则此三角形的最大角与最小角之和为( )A、 B、 C、 D、
-
10、若点是的外心, , 则( )A、1 B、-1 C、3 D、-3
-
11、已知四棱锥的高为2,其底面水平放置时的斜二测画法直观图为平行四边形,如图所示,已知 , , 则四棱锥的体积为( )A、 B、4 C、 D、12
-
12、已知平面向量 , , 则向量在向量上的投影向量是( )A、 B、 C、 D、
-
13、某校高一有1000名学生,为了培养学生良好的阅读习惯,语文教研组要求高一学生从四大名著中选一本阅读,其中有400人选《三国演义》,250人选《水浒传》,250人选《西游记》,100人选《红楼梦》,若采用分层抽样的方法随机抽取100名学生分享他们的读后感,则选《西游记》或《红楼梦》的学生抽取的人数为( )A、25 B、30 C、35 D、50
-
14、已知复数满足(i为虚数单位),则z的虚部为( )A、1 B、 C、 D、
-
15、已知函数 , 其中 .(1)、若在上单调递增,求的取值范围;(2)、当时,若且 , 比较与的大小,并说明理由
-
16、有个正数,排成n行n列的数表:其中表示位于第i行,第j列的数,数表中每一行的数成等差数列,每一列的数成等比数列,并且所有公比相等,已知 , , .(1)、求公比.(2)、求.
-
17、如图,P为圆锥的顶点,为圆锥底面的直径,为等边三角形,O是圆锥底面的圆心.为底面圆O的内接正三角形,且边长为 , 点E为线段中点.
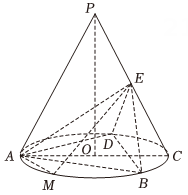 (1)、求证:平面平面;(2)、M为底面圆O的劣弧上一点,且 . 求平面与平面夹角的余弦值.
(1)、求证:平面平面;(2)、M为底面圆O的劣弧上一点,且 . 求平面与平面夹角的余弦值. -
18、在锐角中,内角 , , 的对边分别为 , , , 已知 .(1)、求;(2)、求的取值范围.
-
19、已知四面体 , 其中 , , , 为的中点,则直线与所成角的余弦值为;四面体外接球的表面积为 .
-
20、已知数列的前n项和为 , 且 , , 则( )A、当时, B、 C、数列单调递增,单调递减 D、当时,恒有