相关试卷
-
1、圆锥的底面圆半径 , 侧面的平面展开图的面积为 , 则此圆锥的体积为( )A、 B、 C、 D、
-
2、已知是在上单调递增的奇函数,则函数在上的图象可能为( )A、
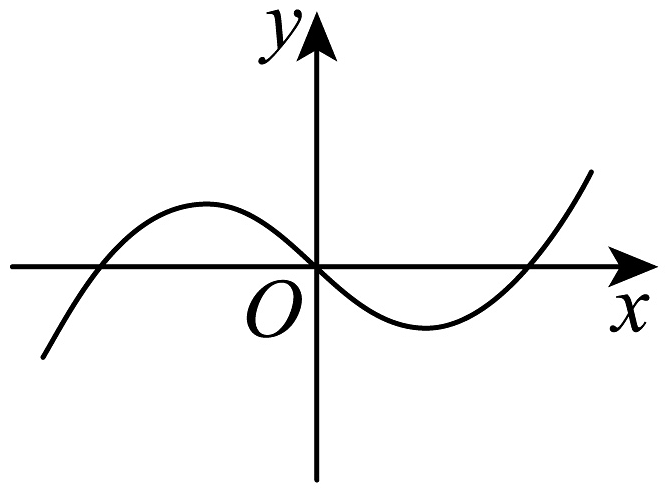 B、
B、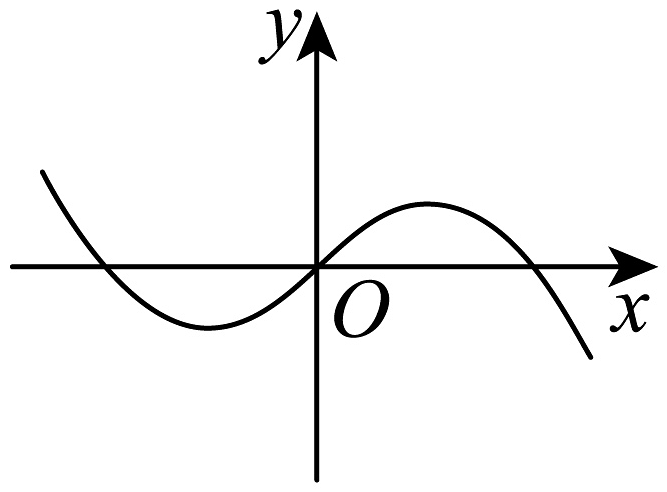 C、
C、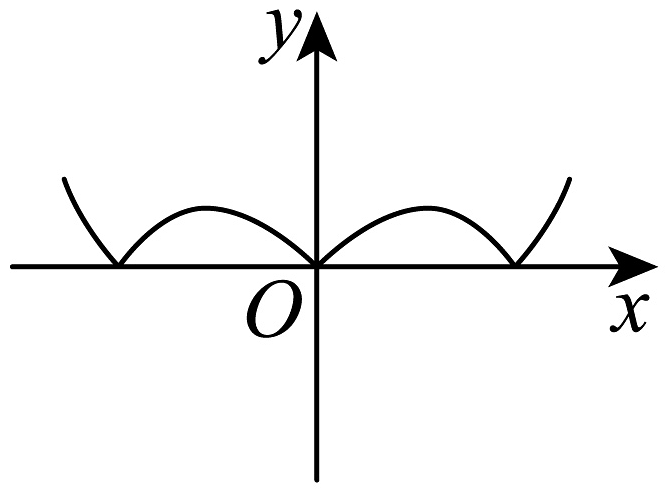 D、
D、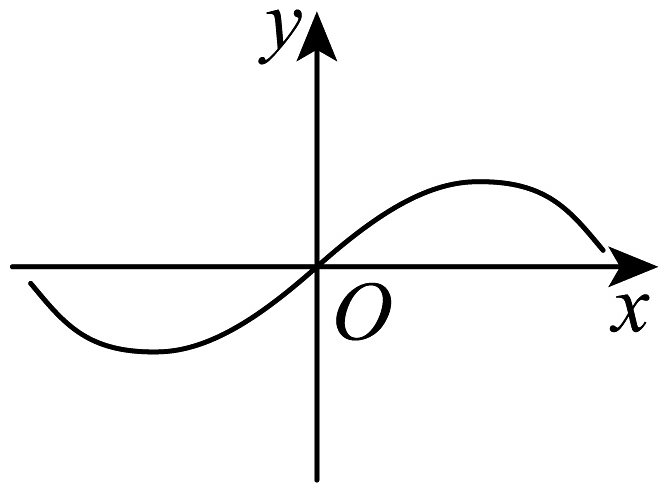
-
3、若平面向量两两的夹角相等,且 , , , 则( )A、1 B、4 C、1或4 D、1或2
-
4、已知复数满足 , 则( )A、 B、1 C、 D、2
-
5、已知函数 , 其中常数.(1)、若在上是增函数,求实数的取值范围;(2)、若 , 设 , 求证:函数在上有两个极值点.
-
6、已知过点的双曲线的渐近线方程为.如图所示,过双曲线的右焦点作与坐标轴都不垂直的直线交的右支于两点.
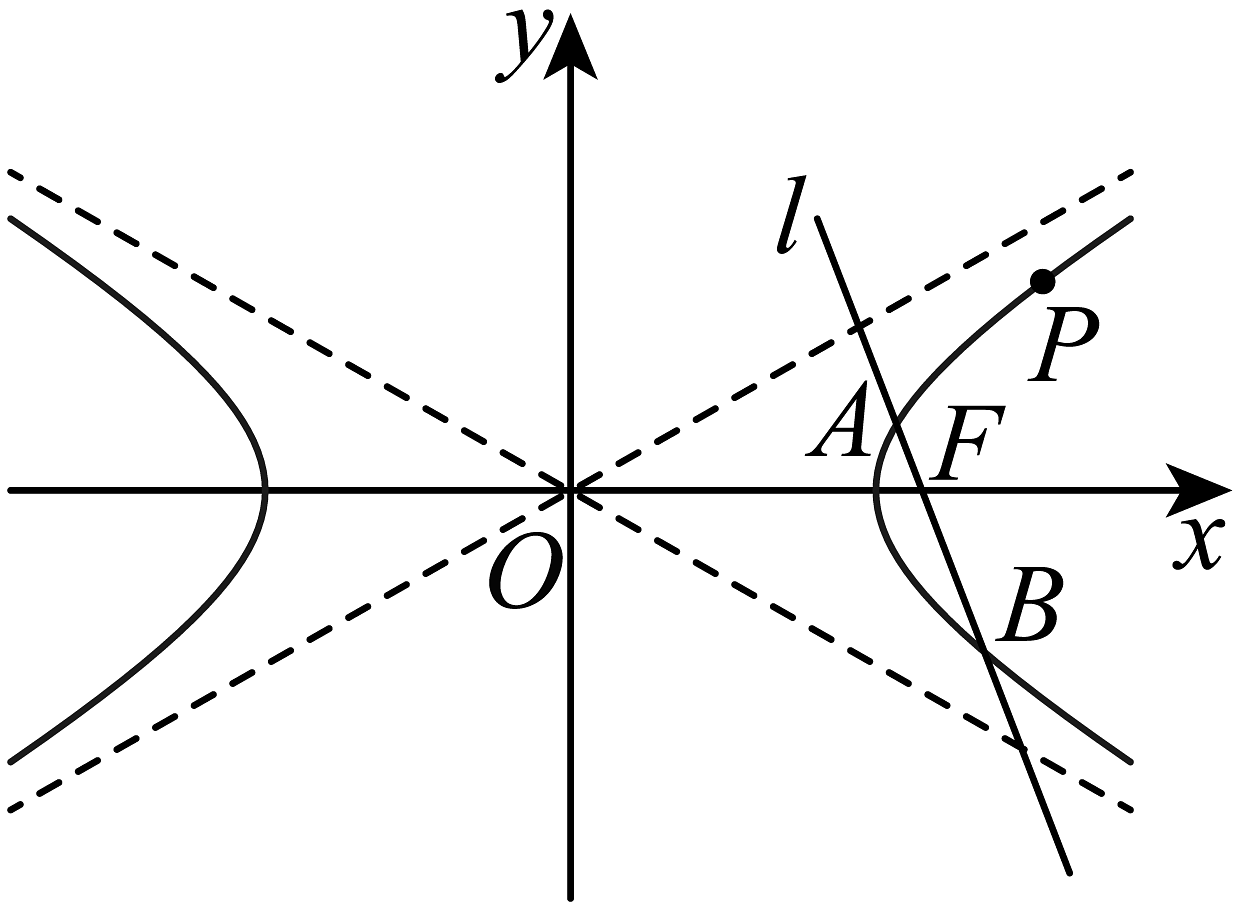 (1)、求双曲线的标准方程;(2)、若双曲线上的点到其两条渐近线的距离分别为 , 求的值;(3)、已知点 , 求证:.
(1)、求双曲线的标准方程;(2)、若双曲线上的点到其两条渐近线的距离分别为 , 求的值;(3)、已知点 , 求证:. -
7、如图,在四棱锥上,底面为直角梯形, , , 平面平面 , 为的中点,是棱上的点, , , .
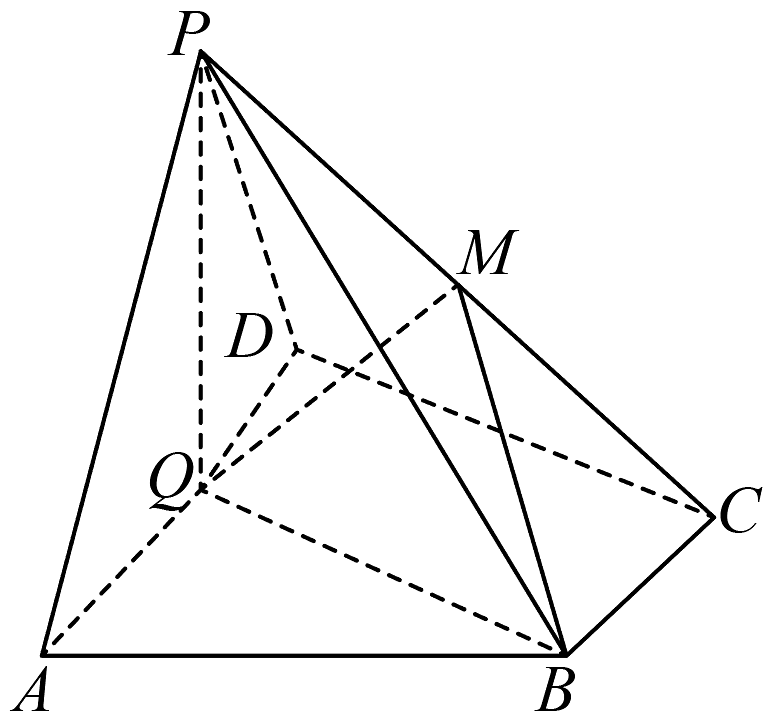 (1)、求证: 平面平面(2)、若二面角大小为 , 求的值
(1)、求证: 平面平面(2)、若二面角大小为 , 求的值 -
8、中,内角的对边分别是 , 已知成等比数列,且 .
(I)求的值;
(II)设 , 求的值.
-
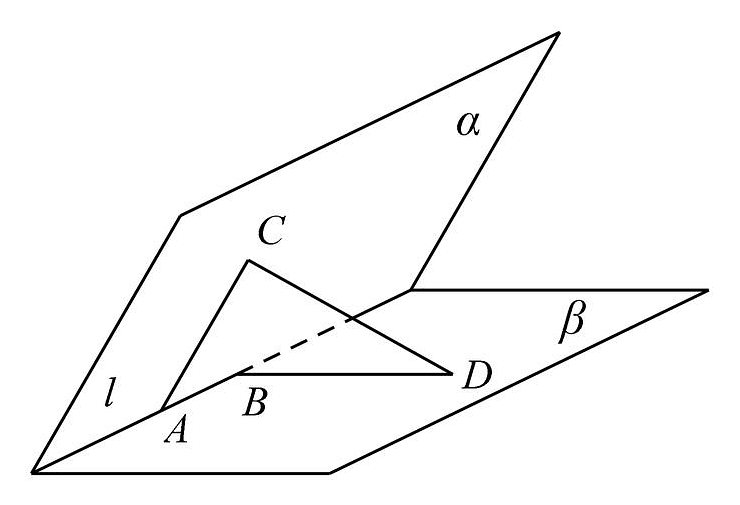
9、如图所示,二面角为 , 是棱上的两点,分别在半平面内 , 且 , , , , , 则的长 .
-
10、已知且 , 则.
-
11、已知在数列中, , , 其前项和为 , 则( )A、当时, B、当时,数列是递增数列 C、 D、对任意 , 存在 , 使得数列成等比数列
-
12、下列说法正确的有( )A、数据的第75百分位数是40 B、若 , 则 C、4名学生选报3门校本选修课,每人只能选其中一门,则总选法数为种 D、展开式中项的二项式系数为56
-
13、已知点是椭圆上的动点,过点作圆的切线,为其中一个切点,则的取值范围为A、 B、 C、 D、
-
14、已知 , 则( )A、 B、 C、 D、
-
15、在中, , 若 , 则的最大值是A、 B、 C、 D、
-
16、两枚骰子,设出现的点数之和分别为9,10,11的概率分别为p1 , p2 , p3 , 则( )A、p1<p2=p3 B、p1>p2>p3 C、p1=p2>p3 D、p1>p2=p3
-
17、已知非常数函数满足 , 则下列函数中,不是奇函数的为( )A、 B、 C、 D、
-
18、已知是虚数单位,则( )A、 B、 C、 D、
-
19、集合A={3,4},B={x| , x∈N}则( )A、 B、 C、 D、
-
20、已知数列的前项和为 , 且.(1)、求数列通项公式;(2)、数列满足 , 求数列的前项和;(3)、设 , 求证:数列中任意不同的三项都不能构成等差数列.