版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、甲参加了一场智力问答游戏，每轮游戏均有两类问题（难度系数较低的 $A$ 类问题以及难度系数较高的 $B$ 类问题）供选择，且每轮游戏只回答两类问题中的其中一个问题．甲遇到每类问题的概率均为 $\frac{1}{2}$ ，甲遇到 $A$ 类问题时回答正确的概率为 $\frac{1}{2}$ ，回答正确记1分，否则记0分；甲遇到 $B$ 类问题时回答正确的概率为 $\frac{1}{4}$ ，回答正确记2分，否则记0分，总得分记为X分，甲回答每个问题相互独立．

(1)、当进行完2轮游戏时，求甲的总分X的分布列与数学期望．

(2)、设甲在每轮游戏中均回答正确且累计得分为n分的概率为 $G (n)$ ．
（ⅰ）证明： $\{G (n + 1) - \frac{1}{2} G (n)\}$ 为等比数列．
（ⅱ）求 $G (n)$ 的最大值以及对应n的值．

查看解析
2、已知抛物线 $C : y^{2} = 2 p x (p > 0)$ 的焦点为F，A，B分别为C上的点（点A在点B上方）．过点A，B分别作C的切线 $l_{1}$ ， $l_{2}$ ，交于点P．点O为坐标原点，当 $△ O A B$ 为正三角形时，其面积为 $48 \sqrt{3}$ ．

(1)、求抛物线C的方程；

(2)、若直线 $A B$ 经过点F，求动点P的轨迹以及点P到直线 $A B$ 的距离的最小值．

查看解析
3、如图，四棱锥 $S - A B C D$ 的底面是边长为2的正方形，每条侧棱的长都是底面边长的 $\sqrt{2}$ 倍，P为侧棱 $S D$ 上的点，且 $S B ∥$ 平面 $P A C$ ．

(1)、求证： $A C ⊥ S D$ ．

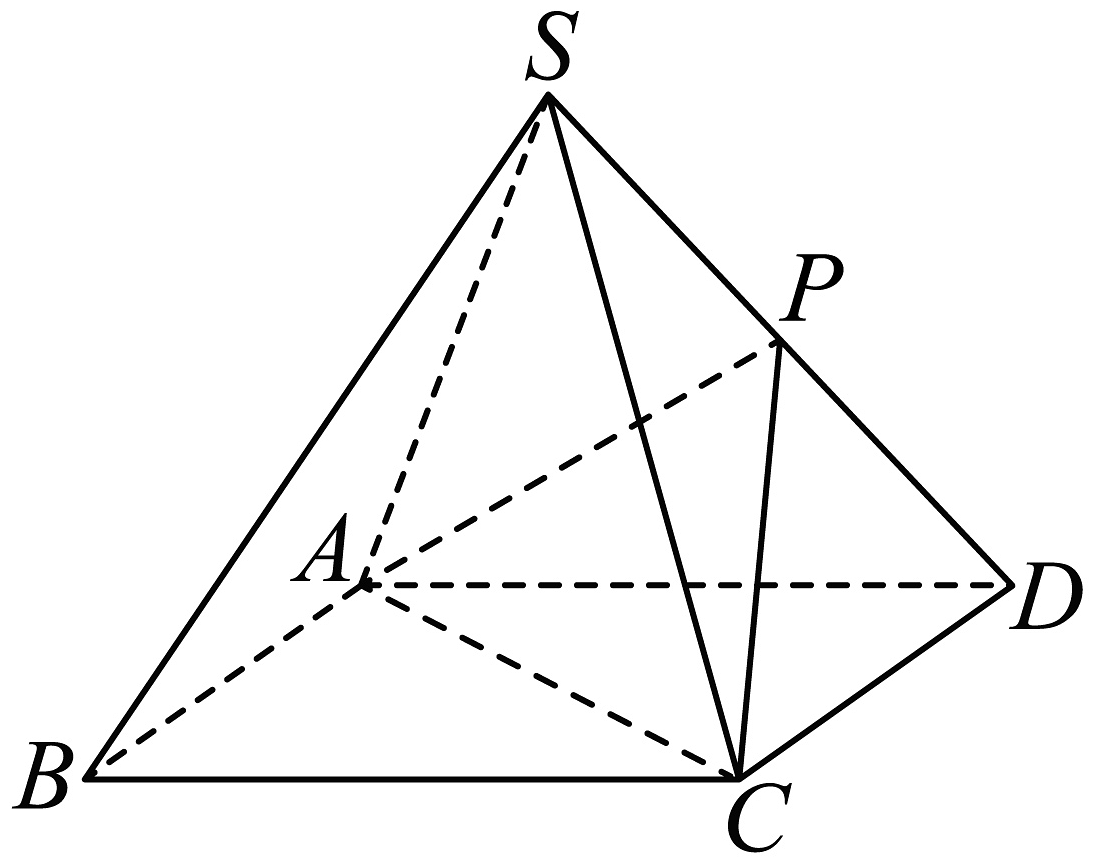(2)、求直线 $S B$ 到平面 $P A C$ 的距离．

(3)、请判断在平面 $P A C$ 上是否存在一点E，使得 $△ E S B$ 是以 $S B$ 为底边， $\frac{2 π}{3}$ 为顶角的等腰三角形．若存在，请求出点E的轨迹；若不存在，请说明理由．

查看解析
4、已知函数 $f (x) = a \ln (x - 1) + x^{2} - 2 x$ ，其中 $a \in R$ ．

(1)、若 $a = - 8$ ，求函数 $f (x)$ 的单调区间；

(2)、当 $a < - 2$ 时，试判断 $f (x)$ 的零点个数并证明．

查看解析
5、在 $△ A B C$ 中，内角A，B，C的对边分别是a，b，c，且 $\sqrt{3} a \sin B + b \cos ∠ B A C = b$ ， D为 $B C$ 边上的点，且 $A D$ 平分 $∠ B A C$ ．

(1)、求 $∠ B A C$ 的大小；

(2)、若 $A D = \frac{15}{8}$ ， $a = 7$ ，求 $△ A B C$ 的周长．

查看解析
6、已知椭圆 $A : \frac{x^{2}}{a_{1}^{2}} + \frac{y^{2}}{b_{1}^{2}} = 1 (a_{1} > b_{1} > 0)$ 与双曲线 $B : \frac{x^{2}}{a_{2}^{2}} - \frac{y^{2}}{b_{2}^{2}} = 1 (a_{2} > 0, b_{2} > 0)$ 具有相同的焦点 $F_{1}$ ， $F_{2}$ ，点P为椭圆A与双曲线B位于第一象限的交点，且 $|O P| = \frac{1}{2} |F_{1} F_{2}|$ （O为坐标原点）．设椭圆A与双曲线B的离心率分别为 $e_{1}$ ， $e_{2}$ ，则 $2 e_{1}^{2} + e_{2}^{2}$ 的最小值为．

查看解析
7、已知 $\tan (α + \frac{π}{12}) = \frac{1}{3}$ ，则 $\sin (2 α + \frac{2 π}{3}) =$ ．

查看解析
8、已知等差数列 $\{a_{n}\}$ 的前n项和为 $S_{n}$ ，且满足 $S_{2 n - 1} = 4 n^{2} - 2 a_{n} - 1$ ， $a_{1} = 1$ ，则数列 $\{a_{n}\}$ 的通项公式为．

查看解析
9、设定义在R上的函数 $f (x)$ 和 $g (x)$ ，记 $g (x)$ 的导函数为 $g^{'} (x)$ ，且满足 $f (x) + g^{'} (x) = 4$ ， $f (x - 1) - g^{'} (3 - x) = 4$ ，若 $g (x)$ 为奇函数，则下列结论一定成立的有（）．

A、 $f (2) + f (4) = 8$ B、 $f (2025) = 4$ C、 $\sum_{n = 1}^{2025} f (n) = 8100$ D、 $g^{'} (4) = 0$

查看解析
10、复数 $z_{1}$ ， $z_{2}$ 满足 $z_{1} + z_{2} = 4$ ， $z_{1} \cdot z_{2} = 8$ ，则（）．

A、 $|z_{1}| \cdot |z_{2}| = 8$ B、 $|z_{1} - z_{2}| = 4$ C、 $|z_{1}| + |z_{2}| = 4$ D、 $|\frac{z_{1}}{z_{2}}| = 1$

查看解析
11、已知 $A (1, 6)$ ， $B (2, 4)$ ， $C (3, 4)$ ， $D (4, 2)$ ， $E (5, 4)$ ， 5个数据的散点图如图所示，采用一元线性回归模型建立经验回归方程．经分析确定 $E (5, 4)$ 为“离群点”，故将其去掉，将数据 $E (5, 4)$ 去掉后，下列说法正确的有（）．

A、样本相关系数r变大 B、残差平方和变小 C、决定系数 $R^{2}$ 变大 D、若经验回归直线过点 $(3.5, 2.8)$ ，则其经验回归方程为 $\hat{y} = - 1.2 x + 7$

查看解析
12、已知定义在 $R$ 上的函数 $f (x)$ 为奇函数，且当 $x > 0$ 时， $f (x) = e^{x} - a$ ，若 $\forall x \in R$ ，不等式 $f (- x) + f (x - |a - 1|) \leq 0$ 恒成立，则 $a$ 的值不可能是（）．

A、 $- 2025$ B、 $2025$ C、 $e^{2}$ D、3

查看解析
13、已知 $A (- 1, 0)$ ， $B (1, 0)$ ，点P满足 $|P A| = \sqrt{3} |P B|$ ，当 $∠ P A B$ 取到最大值时， $△ P A B$ 的面积为（）．

A、 $\frac{3 \sqrt{3}}{4}$ B、 $\frac{3 \sqrt{2}}{4}$ C、 $\frac{3 \sqrt{2}}{2}$ D、 $\sqrt{2}$

查看解析
14、已知函数 $f (x) = \sin (2 x + \frac{π}{6})$ 在区间 $(0, m)$ 上存在唯一个极大值点，则m的最大值为（）．

A、 $\frac{7 π}{6}$ B、 $π$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看解析
15、一个圆锥的侧面展开图是一个半径为3，圆心角为 $\frac{2 π}{3}$ 的扇形，在该圆锥内有一个体积为V的球，则该球的体积V的最大值是（）．

A、 $2 π$ B、 $\frac{2}{3} π$ C、 $\frac{2 \sqrt{2}}{3} π$ D、 $\frac{\sqrt{2}}{3} π$

查看解析
16、一组数据1，3，7，9， $m (m > 0)$ 的中位数不小于平均数，则m的取值范围为（）．

A、 $[5, 7]$ B、 $[5, 15]$ C、 $[7, 15]$ D、 $[5, 20]$

查看解析
17、在等比数列 $\{a_{n}\}$ 中， $a_{3} \cdot a_{5} = 49$ ， $a_{4} + a_{6} = 70$ ，则 $a_{8} =$ （）．

A、 $- 567$ B、567 C、451 D、699

查看解析
18、已知向量 $\vec{a} = (- 1, \frac{1}{2})$ ， $\vec{b} = (1, m)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $|\vec{b}| =$ （）．

A、 $\sqrt{3}$ B、2 C、 $\sqrt{5}$ D、5

查看解析
19、已知集合 $A = \{x |x^{2} + 2 x \leq 0\}$ ， $B = [- 1, 1]$ ，则 $A \cap B =$ （）．

A、 $[- 1, 0]$ B、 $[- 2, 1]$ C、 $\emptyset$ D、 $\{- 1, 0\}$

查看解析
20、对于数列 $\{a_{n}\}$ ，称 $\{Δ a_{n}\}$ 为数列 $\{a_{n}\}$ 的一阶差分数列，其中 $Δ a_{n} = a_{n + 1} - a_{n} (n \in N^{*})$ .对正整数 $k (k \geq 2)$ ，称 $\{Δ^{k} a_{n}\}$ 为数列 $\{a_{n}\}$ 的 $k$ 阶差分数列，其中 $Δ^{k} a_{n} = Δ (Δ^{k - 1} a_{n}) = Δ^{k - 1} a_{n + 1} - Δ^{k - 1} a_{n}$ 已知数列 $\{a_{n}\}$ 的首项 $a_{1} = 1$ ，且 $\{Δ a_{n + 1} - a_{n} - 2^{n}\}$ 为 $\{a_{n}\}$ 的二阶差分数列.

(1)、求数列 $\{a_{n}\}$ 的通项公式；

(2)、设 $b_{n} = \frac{1}{2} (n^{2} - n + 2), \{x_{n}\}$ 为数列 $\{b_{n}\}$ 的一阶差分数列，对 $\forall n \in N^{*}$ ，是否都有 $\sum_{i = 1}^{n} x_{i} C_{n}^{i} = a_{n}$ 成立？并说明理由；（其中 $C_{n}^{i}$ 为组合数）

(3)、对于（2）中的数列 $\{x_{n}\}$ ，令 $y_{n} = \frac{t^{x_{n}} + t^{- x_{n}}}{2}$ ，其中 $\frac{1}{2} < t < 2$ .证明： $\sum_{i = 1}^{n} y_{i} < 2^{n} - 2^{- \frac{n}{2}}$ .

查看解析

上一页 403 404 405 406 407 下一页跳转