相关试卷
-
1、函数的值域是( )A、 B、 C、 D、
-
2、一游戏规则如下:一个质点在数轴上运动,从原点出发,每次向左或者向右移动一个单位,共移动了次.(1)、已知质点每次向右移动的概率为.
①当 时,求质点最终回到原点的概率;
②规定质点在运动过程中,只要出现在原点左侧,游戏就结束,否则游戏就继续、直到移动了次,分别求出当和时质点最终落在原点右侧的概率并比较它们的大小
(2)、现在规定游戏分为两个阶段:第一阶段,质点每次向右移动的概率为、共移动了3次、若质点最终落在了原点左侧,则结束游戏,且最终得分为0分. 若最终落在了原点右侧、则通过第一阶段,并进入第二阶段:质点重新回到原点,每次向右移动的概率为 , 并再次移动了3次,若质点最终落在了原点左侧,则最终得分也为0分; 若最终落在了原点右侧,则最终得分为质点位于数轴上所在位置对应的实数.①请用含的式子表示该游戏得分的数学期望;
②若 则当取何值的时候,该游戏得分的期望值最大?
-
3、已知函数 , .(1)、若在区间上最大值为2,求实数的值;(2)、当时,求不等式的解集.
-
4、在四棱锥中,底面 , , , , , 点为棱中点.
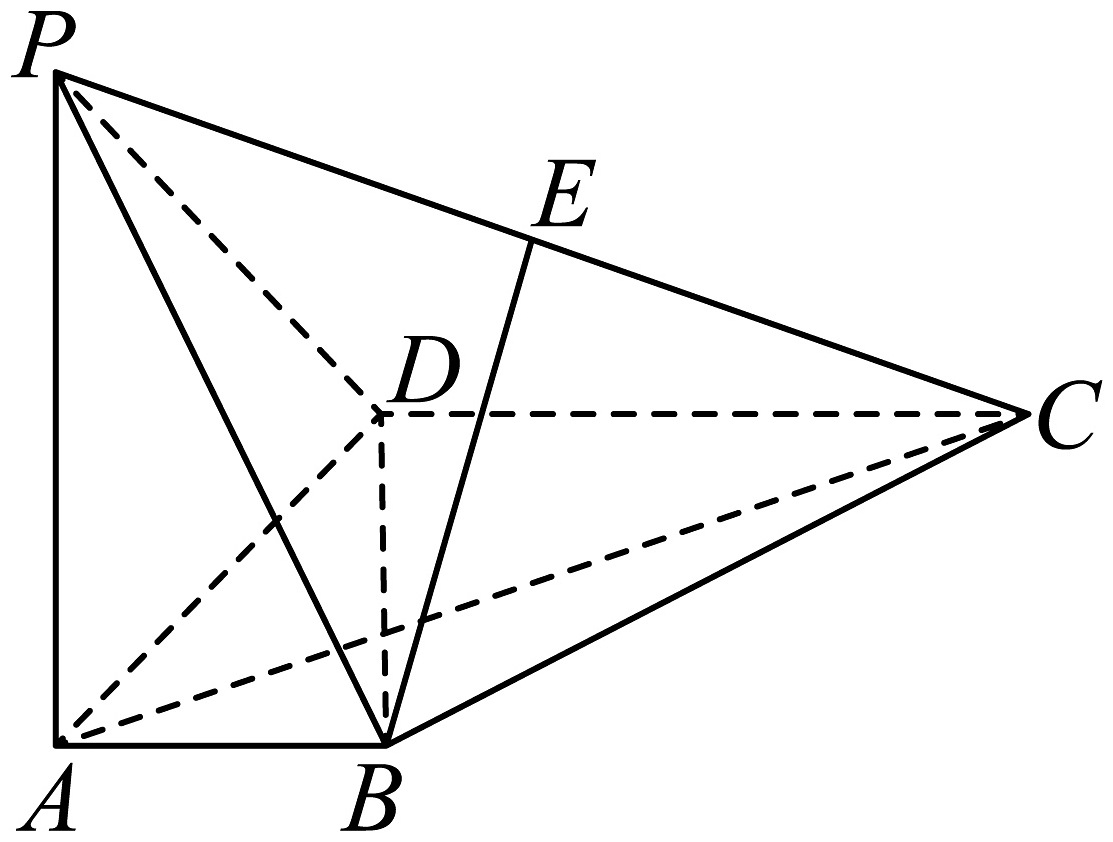 (1)、证明:平面;(2)、求直线与平面所成角的正弦值;(3)、若为棱上一点,满足 , 求平面与平面夹角的余弦值.
(1)、证明:平面;(2)、求直线与平面所成角的正弦值;(3)、若为棱上一点,满足 , 求平面与平面夹角的余弦值. -
5、如图,平行六面体中,AC与BD交于点M,设 , , , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、下列各组函数表示同一函数的是( )A、 B、 C、 D、
-
7、由直线上的一点向圆引切线,切点为 , 则的最小值为.
-
8、已知直线经过点 , 且是的方向向量,则点到的距离为 .
-
9、已知 , 分别是平面 , 的法向量,且 , 则t的值为( )A、1 B、2 C、 D、
-
10、设数列的前项和为 , 已知 , 则下列结论正确的是( )A、 B、数列为等比数列 C、 D、若 , 则数列的前10项和为
-
11、已知数列的前n项和为 , , .(1)、证明:数列为等差数列,并求数列的通项公式;(2)、求数列的前n项和为;(3)、若对任意恒成立.求实数的取值范围.
-
12、已知R , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
13、表示大于或者等于的最小整数,表示小于或者等于的最大整数.设为的单调递增数列,且满足 , 则下列选项正确的是( )A、 B、至多有种取值可能 C、 D、
-
14、直线 , 点 , , 若与线段AB相交,则的范围为( )A、 B、 C、 D、
-
15、已知函数的图象过点 , 且满足 .(1)、求函数的解析式;(2)、设函数在上的最小值为 , 求的值域;(3)、若满足 , 则称为函数的不动点.函数有两个不相等的不动点 , 且 , 求的最小值.
-
16、如图,在平行六面体中,以顶点A为端点的三条棱长都是1,且它们彼此的夹角都是60°,M为与的交点,若 , 则下列正确的是( )
 A、 B、 C、的长为 D、
A、 B、 C、的长为 D、 -
17、古希腊数学家阿波罗尼奥斯用不同的平面截同一圆锥,得到了圆锥曲线,其中的一种如图所示.用过M点且垂直于圆锥底面的平面截两个全等的对顶圆锥得到双曲线的一部分,已知高 , 底面圆的半径为8,M为母线PB的中点,平面与底面的交线 , 则双曲线的两条渐近线的夹角的余弦值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、已知点是直线上的动点,过点引圆的两条切线为切点,当的最大值为 , 则的值为( )A、4 B、 C、1 D、
-
19、设 , 则“”是“且”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
-
20、记为为不超过m的最大整数,设函数(且),求的值域.