版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、如图，正方形 $A B C D$ 的边长为1， $E$ ， $F$ 分别是 $A D$ 和 $B C$ 边上的点.沿 $E F$ 折叠使 $C$ 与线段 $A B$ 上的 $M$ 点重合（ $M$ 不在端点 $A, B$ 处），折叠后 $C D$ 与 $A D$ 交于点 $G$ .

(1)、证明： $△ A M G$ 的周长为定值.

(2)、求 $△ A M G$ 的面积 $S$ 的最大值.

查看解析
2、已知函数 $f (x), g (x)$ 的定义域为 $R, y = f (x)$ 的图象关于直线 $x = 1$ 对称，且 $f (1 - x) + g (x) = 10$ ， $f (x) - g (x - 4) = 5$ ，若 $f (2) = 1$ ，则 $g (1) + g (2) =$ .

查看解析
3、函数 $f (x) = \{\begin{array}{l} x^{2} + x, 0 < x < 2 \\ - 2 x + 8, x \geq 2 \end{array}$ ，若 $f (a) = f (a + 2)$ ，则 $f (2 a) =$ .

查看解析
4、定义在 $R$ 上的偶函数 $f (x)$ 满足： $f (2) = 2$ ，且对于任意 $x_{1} > x_{2} > 0$ ， $x_{2} f (x_{1}) - x_{1} f (x_{2}) > 2 x_{2} - 2 x_{1}$ ，若函数 $g (x) = \frac{f (x) - 2}{x}$ ，则下列说法正确的是（）

A、 $g (x)$ 在 $(0, + \infty)$ 上单调递增 B、 $g (- 3) < g (4)$ C、 $f (x)$ 在 $(2, + \infty)$ 上单调递减 D、若正数 $m$ 满足 $f (2 m) - \frac{m}{2} f (4) + m - 2 > 0$ ，则 $m \in (2, + \infty)$

查看解析
5、已知a，b为正实数，且 $a b + a + b = 8$ ，则（）

A、 $a b$ 的最大值为4 B、 ${(a + 1)}^{2} + {(b + 1)}^{2}$ 的最小值为18 C、 $a + b$ 的最小值为4 D、 $\frac{1}{a + 1} + \frac{1}{b + 1}$ 的最小值为 $\frac{\sqrt{2}}{2}$

查看解析
6、对于任意实数 $a$ ， $b$ ， $c$ ， $d$ ，下列四个命题中为假命题的是（）

A、若 $a > b$ ， $c \neq 0$ ，则 $a c > b c$ B、若 $a c^{2} > b c^{2}$ ，则 $a > b$ C、若 $a < b < 0$ ，则 $a^{2} > a b > b^{2}$ D、若 $a > b > 0$ ， $c > d$ ，则 $a c > b d$

查看解析
7、已知函数 $f (x)$ 是定义在 $[0, + \infty)$ 的单调函数，且对于任意的 $x \in [0, + \infty)$ ，都有 $f [f (x) - \sqrt{x}] = 2$ ，若关于 $x$ 的方程 $f (x + 2) = x + k$ 恰有两个实数根，则实数 $k$ 的取值范围为（）

A、 $[2, \frac{9}{4})$ B、 $[1, \frac{5}{4})$ C、 $[3, \frac{13}{4})$ D、 $(- \infty, \frac{13}{4})$

查看解析
8、“函数 $f (x) = \frac{1}{a x^{2} - a x + 1}$ 的定义域为R”是“ $0 < a < 4$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看解析
9、已知 $f (x) = a x^{2} - x - c$ ，若 $f (x) > 0$ 的解集为 $(- 2, 1)$ ，则函数 $y = f (- x)$ 的大致图象是（）

A、 B、 C、 D、

查看解析
10、下列函数既是奇函数又在 $(0, + \infty)$ 单调递增的是（）

A、 $y = \frac{1}{x}$ B、 $y = \frac{1}{x^{3}}$ C、 $y = x - \frac{1}{x}$ D、 $y = x + \frac{1}{x}$

查看解析
11、已知集合 $A = \{x ∣ x^{2} - 3 x + 2 = 0\}, B = {x ∣ (x - 2) (a x - 2) = 0}$ ，若 $A \cup B = A$ ，则实数 $a$ 的值不可以为（）

A、2 B、1 C、0 D、 $- 1$

查看解析
12、已知函数 $f (x) = x^{2} + 2 a x - b$ ．
（1）若 $b = 3 a^{2}$ ，求不等式 $f (x) \leq 0$ 的解集；
（2）若 $a > 0, b > 0$ ，且 $f (b) = b^{2} + b + a + 1$ ，求 $a + b$ 的最小值．

查看解析
13、已知 $y = f (x)$ 是定义在 $R$ 上的奇函数，当 $x \geq 0$ 时， $f (x) = - x^{2} + 2 x$ ．

(1)、求函数 $f (x)$ 的解析式，画出函数 $f (x)$ 的图像并写出函数的单调区间；

(2)、若函数 $f (x)$ 在区间 $[- 1, a - 2]$ 上单调递增，求实数 $a$ 的取值范围；

(3)、若方程 $| f (x) | - k = 0$ 有 $2$ 个根，求实数 $k$ 的取值范围，并求这 $2$ 个根的和

查看解析
14、已知连续函数 $f (x)$ 对任意实数 $f (x)$ 恒有 $f (x + y) = f (x) + f (y)$ ，当 $x > 0$ 时， $f (x) < 0, f (1) = - 2$ ，则以下说法中正确的是（）

A、 $f (0) = 0$ B、 $f (x)$ 是R上的奇函数 C、 $f (x)$ 在 $[- 3, 3]$ 上的最大值是8 D、不等式 $f (3 x^{2}) - 2 f (x) < f (3 x) + 4$ 的解集为 $\{x |x < \frac{2}{3} 或 x > 1\}$

查看解析
15、已知全集 $U = R$ ，实数 $a, b$ 满足 $a > b > 0$ ，集合 $M = \{x |b < x < \frac{a + b}{2}\}$ ， $N = {x| \sqrt{a b} < x < a}$ ，则 $M \cap ∁_{U} N =$ .

查看解析
16、命题“ $\exists x \in R$ ， $x^{3} + |x| - 2 > 0$ ”的否定是（）

A、 $\exists x \notin R$ ， $x^{3} + |x| - 2 \leq 0$ B、 $\exists x \in R$ ， $x^{3} + |x| - 2 \leq 0$ C、 $\forall x \in R$ ， $x^{3} + |x| - 2 \leq 0$ D、 $\forall x \notin R$ ， $x^{3} + |x| - 2 \leq 0$

查看解析
17、已知 $△ A B C$ 的顶点分别为 $A (2, 4)$ ， $B (7, - 1)$ ， $C (- 6, 1)$ .

(1)、求 $B C$ 边的中线 $A D$ 所在直线的方程；

(2)、求 $B C$ 边的垂直平分线 $D E$ 的方程.

查看解析
18、已知命题 $p : \forall x \in R$ ， $x^{2} + 1 > 0$ ；命题 $q : \exists x < 0$ ， $|x| = x$ ，则（）

A、 $p$ 和 $q$ 都是真命题 B、 $\neg p$ 和 $q$ 都是真命题 C、 $p$ 和 $\neg q$ 都是真命题 D、 $\neg p$ 和 $\neg q$ 都是真命题

查看解析
19、 $△ A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，已知 $2 a + b = 2 c cos B$ ．

(1)、求角 $C$ ；

(2)、若角 $C$ 的平分线 $C D$ 交 $A B$ 于点 $D, A D = 3 \sqrt{13}, D B = \sqrt{13}$ ，求 $C D$ 的长．

查看解析
20、如图，四边形 $A B C D$ 为菱形， $P B ⊥$ 平面 $A B C D$ ．

(1)、证明：平面 $P A C ⊥$ 平面 $P B D$ ；

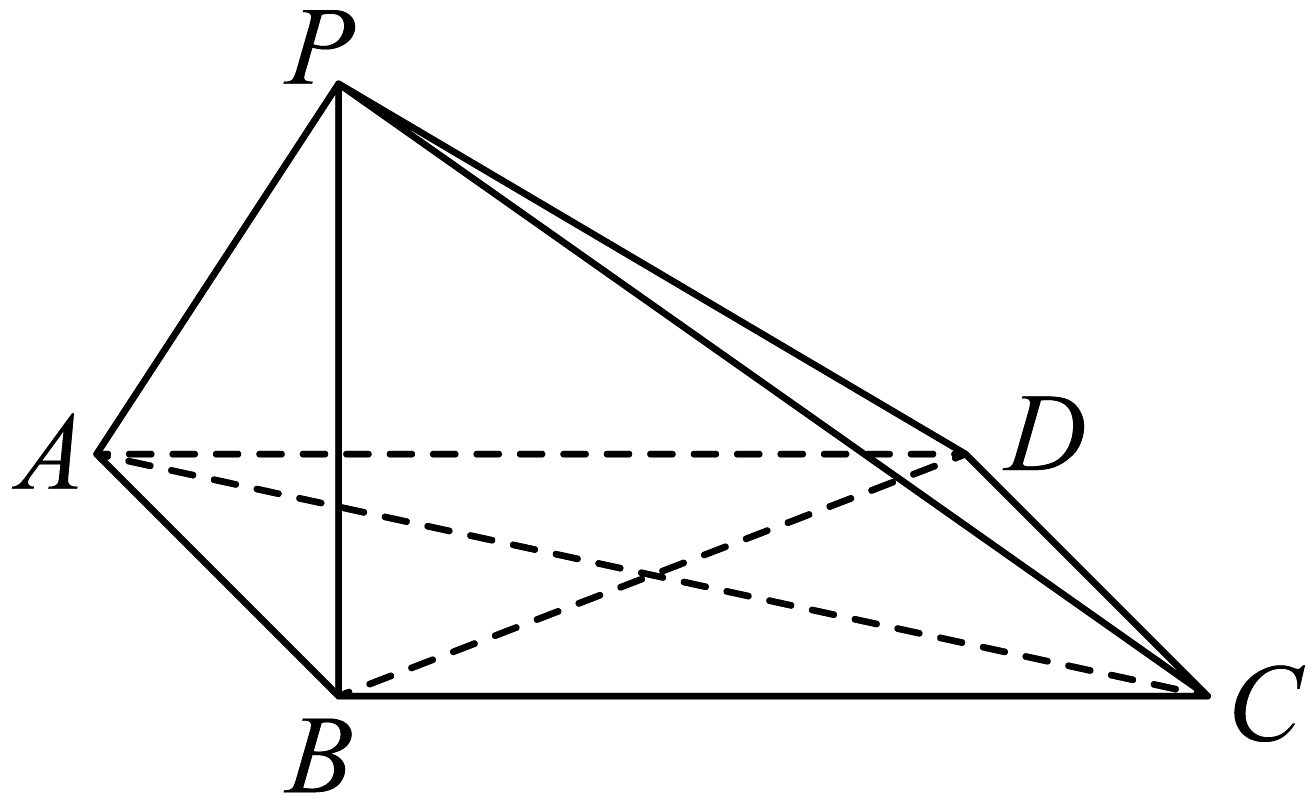(2)、若 $P A ⊥ P C$ ，二面角 $A - B P - C$ 的大小为120°，求PC与BD所成角的余弦值．

查看解析

上一页 944 945 946 947 948 下一页跳转