版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 为 $A A_{1}$ 的中点，点 $F$ 满足 $\vec{A_{1} F} = λ \vec{A_{1} B_{1}} (0 \leq λ \leq 1)$ ，则（）

A、当 $λ = 0$ 时， $A C_{1} ⊥$ 平面 $B D F$ B、任意 $λ \in [0, 1]$ ，三棱锥 $F - B D E$ 的体积是定值 C、存在 $λ \in [0, 1]$ ，使得 $A C$ 与平面 $B D F$ 所成的角为 $\frac{π}{3}$ D、当 $λ = \frac{2}{3}$ 时，平面 $B D F$ 截该正方体的外接球所得截面的面积为 $\frac{56}{19} π$

查看解析
2、设命题 $p$ ：关于 $x$ 的方程 $x^{2} + m x + 1 = 0$ 有两个不相等的实数根， $q$ ：关于 $x$ 的方程 $4 x^{2} + (4 m - 2) x + 1 = 0$ 无实数根．

(1)、若 $p$ 为真，求实数 $m$ 的取值范围；

(2)、若 $p$ 、 $q$ 有且仅有一个为真命题，求实数m的取值范围．

查看解析
3、已知函数 $f (x) = \sqrt{x + 5} + \frac{1}{x - 7}$
（1）求函数的定义域；
（2）求 $f (11)$ ， $f (\frac{5}{4})$ 的值；
（3）当 $a > 0$ 时，求 $f (a)$ ， $f (a - 1)$ 的值．

查看解析
4、已知 $x > 1$ ，函数 $y = x + \frac{1}{x - 1}$ 的最小值是（）

A、3 B、4 C、5 D、6

查看解析
5、已知命题 $p : \exists x < 1, x^{2} \leq 1$ ，则命题 $p$ 的否定为（）

A、 $\forall x \geq 1, x^{2} > 1$ B、 $\exists x < 1, x^{2} > 1$ C、 $\forall x < 1, x^{2} > 1$ D、 $\exists x \geq 1, x^{2} > 1$

查看解析
6、如图，在四棱锥 $P - A B C D$ 中，平面 $P A D ⊥$ 平面 $A B C D, P A ⊥ P D, A B ⊥ A D, P A = P D$ ， $A B = 1, A D = 2, A C = C D = \sqrt{5}$ ．

(1)、求证： $P D ⊥$ 平面PAB；

(2)、求直线PB与平面PCD所成角的正弦值；

(3)、在棱AP上是否存在点 $M$ ，使得平面MBC与平面PCD所成角余弦值为 $\frac{5 \sqrt{11}}{33}$ ?若存在，求出 $\frac{A M}{A P}$ 的值；若不存在，请说明理由．

查看解析
7、如图，从参加环保知识竞赛的学生中抽出 $60$ 名，将其成绩（均为整数）整理后画出的频率分布表和频率分布直方图如下，回答下列问题：
分组
人数
频率
$[40, 50)$
$a$
$0.10$
$[50, 60)$
$9$
$x$
$[60, 70)$
$b$
$0.15$
$[70, 80)$
$18$
$0.30$
$[80, 90)$
$15$
$y$
$[90, 100]$
$3$
$0.05$

(1)、分别求出 $a, b, x, y$ 的值，并补全频率分布直方图；

(2)、估计这次环保知识竞赛平均分；

(3)、从成绩在 $[40, 50)$ 和 $[90, 100]$ 的两组学生中按分层抽样的方式抽取 $3$ 人，再从这 $3$ 人中随机抽取 $2$ 人，求抽取的 $2$ 人中成绩都在 $[40, 50)$ 的概率．

查看解析
8、如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P A ⊥$ 平面 $A B C D$ ， $E$ 为 $P D$ 上的中点．

(1)、证明 $P B / /$ 平面 $A E C$ ；

(2)、设 $P A = A B = 2$ ，求三棱锥 $E - P B C$ 的体积．

查看解析
9、已知两个点的坐标 $A (1, 2), B (5, 0)$ ．

(1)、求过点 $C (3, 4)$ 且与直线AB垂直的直线 $l$ 的方程；

(2)、若四边形 $A B C D$ 是平行四边形，求点 $D$ 的坐标．

查看解析
10、在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，已知 $a sin B + \sqrt{3} b cos A = 0$ ．

(1)、求角 $A$ 的大小；

(2)、若 $a = 7$ ，且 $c sin A = \frac{5}{2} \sqrt{3}$ ，求 $△ A B C$ 的面积．

查看解析
11、已知矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，现沿 $A C$ 折起，使得平面 $A B C ⊥$ 平面 $A D C$ ，连接 $B D$ ，得到三棱锥 $B - A C D$ ，则其外接球的体积为．

查看解析
12、经过点 $A (2, - 1)$ 且与x轴垂直的直线l的方程为．

查看解析
13、如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，E为棱 $D D_{1}$ 的中点， $P$ 为底面正方形 $A B C D$ 内（含边界）的动点，则（）

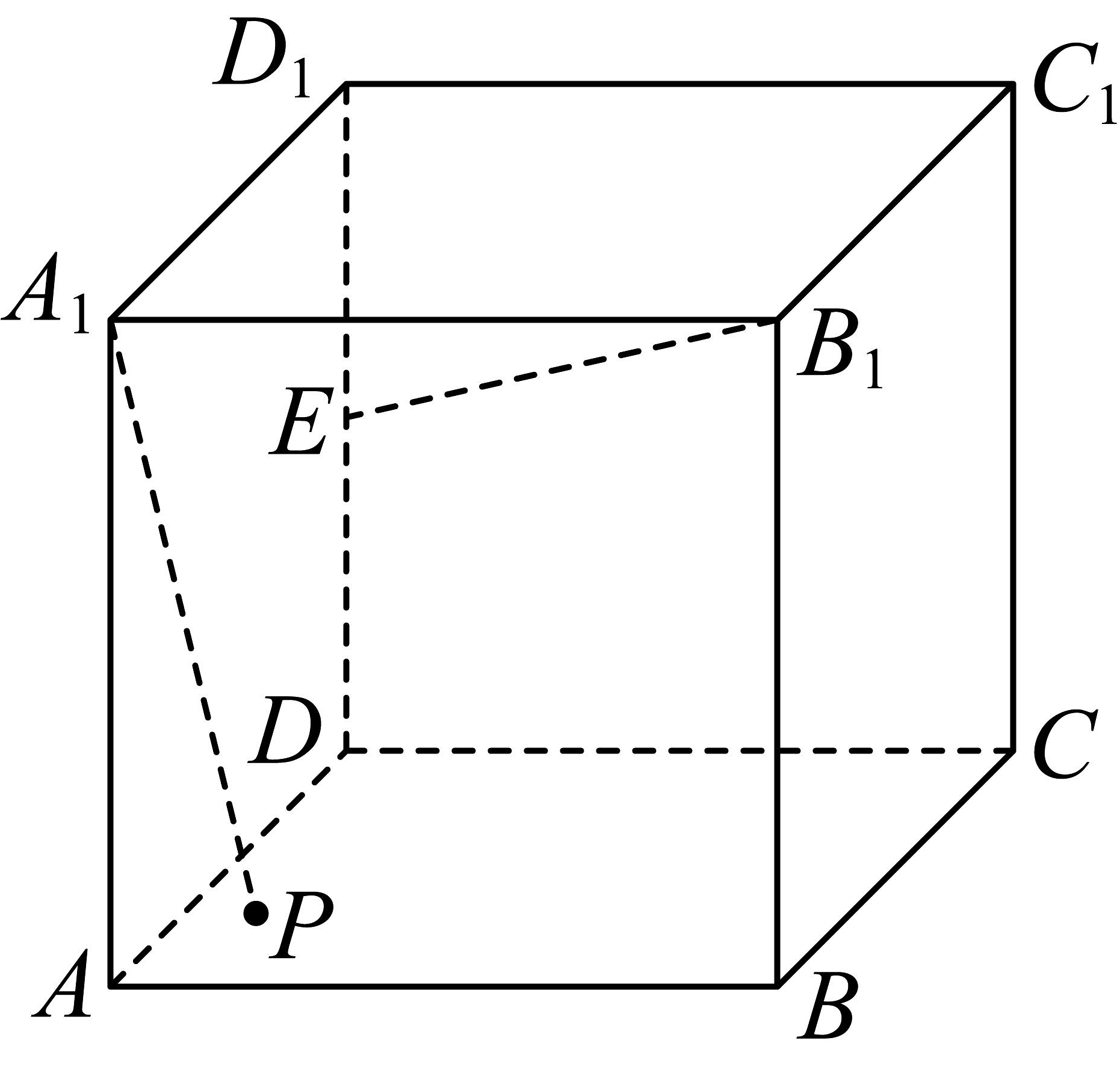A、三棱锥 $B_{1} - A_{1} D_{1} P$ 的体积为定值 B、直线 $B_{1} E / /$ 平面 $A_{1} B D$ C、当 $A_{1} P ⊥ B D$ 时，点 $E$ 到平面 $A_{1} A P$ 的距离为 $\frac{\sqrt{2}}{2}$ D、当 $∠ A P A_{1}$ 的正切值为2时，动点P的轨迹长度为 $\frac{π}{4}$

查看解析
14、某超市在两周内的蓝莓每日促销量如图所示，根据此折线图，下面结论正确的是（）

A、这14天日促销量的众数是214 B、这14天日促销量的中位数是196 C、这14天日促销量的极差为195 D、这14天日促销量的第80百分位数是243

查看解析
15、设点 $A (4, - 3), B (- 2, - 2)$ ，直线 $l$ 过点 $P (1, 1)$ 且与线段 $A B$ 相交，则直线 $l$ 的斜率 $k$ 的取值范围是（）

A、 $k \geq 1$ 或 $k \leq - 4$ B、 $k \geq 1$ 或 $k \leq - \frac{4}{3}$ C、 $- 4 \leq k \leq 1$ D、 $- \frac{4}{3} \leq k \leq 1$

查看解析
16、若直线 $l_{1} : a x + 3 y + 2 = 0$ 与直线 $l_{2} : x - (a + 1) y + a = 0$ 垂直，则实数 $a =$ （）

A、0 B、1 C、 $- \frac{3}{4}$ D、 $- \frac{3}{2}$

查看解析
17、在 $△ A B C$ 中，角A，B，C所对的边分别是a，b，c，若 $b \cos A + a \cos B = c \sin C$ ，则 $△ A B C$ 为（）.

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看解析
18、已知点 $A (- 3, 1, 4)$ ，则点A关于x轴对称的点的坐标为（）

A、 $(3, - 1, - 4)$ B、 $(1, - 3, 4)$ C、 $(- 3, - 1, - 4)$ D、 $(4, - 1, 3)$

查看解析
19、已知 $3 < x < 7, 1 < y < 2$ ，则 $\frac{y}{x}$ 的取值范围是.

查看解析
20、已知实数 $x, y > 0$ ，且 $\frac{2}{x} + \frac{1}{y} = 1$ ，若 $2 x + y > m^{2} - 8 m$ 恒成立，则实数 $m$ 的取值范围为（）

A、 $(- 9, 1)$ B、 $(- 1, 9)$ C、 $[- 1, 9]$ D、 $(- \infty, - 1) \cup (9, + \infty)$

查看解析

上一页 940 941 942 943 944 下一页跳转

分组	人数	频率
$[40, 50)$	$a$	$0.10$
$[50, 60)$	$9$	$x$
$[60, 70)$	$b$	$0.15$
$[70, 80)$	$18$	$0.30$
$[80, 90)$	$15$	$y$
$[90, 100]$	$3$	$0.05$