-
1、已知复数满足: , 则.
-
2、如图,一条河两岸平行,河的宽度 , 一艘船从河岸边的A地出发,向河对岸航行.已知船在静水中的速度的大小 , 水流方向为正东方向,其速度的大小为 , 这艘船到达河对岸的时间精确到0.1min,采用四舍五入法.则( )
参考数据:
 A、这艘船到达河对岸的渡河时间最短时, B、这艘船到达河对岸的渡河时间最短为3min C、这艘船到达河对岸的渡河时间最短为3.1min D、这艘船到达河对岸的航程最短时,渡河时间最短
A、这艘船到达河对岸的渡河时间最短时, B、这艘船到达河对岸的渡河时间最短为3min C、这艘船到达河对岸的渡河时间最短为3.1min D、这艘船到达河对岸的航程最短时,渡河时间最短 -
3、函数在一个周期内的图象如图所示,则( ).
 A、该函数的解析式为 B、该函数图象的对称轴方程为 , C、该函数的单调递增区间是 , D、把函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象
A、该函数的解析式为 B、该函数图象的对称轴方程为 , C、该函数的单调递增区间是 , D、把函数的图象上所有点的横坐标伸长为原来的倍,纵坐标不变,可得到该函数图象 -
4、“虚数”这个词是世纪著名数学家、哲学家笛卡尔创制的,当时的观念认为这是不存在的数.人们发现即使使用全部的有理数和无理数,也不能解决代数方程的求解问题,像这样最简单的二次方程,在实数范围内没有解.引进虚数概念以后,代数方程的求解问题才得以解决.设是方程的根,则( )A、 B、 C、是该方程的根 D、是该方程的根
-
5、已知“水滴”的表面是一个由圆锥的侧面和部分球面(常称为“球冠”)所围成的几何体.如图所示,将“水滴”的轴截面看成由线段和优弧所围成的平面图形,其中点所在直线与水平面平行,和与圆弧相切.已知“水滴”的“竖直高度”与“水平宽度”(“水平宽度”指的是平行于水平面的直线截轴截面所得线段的长度的最大值)的比值为 , 则( )
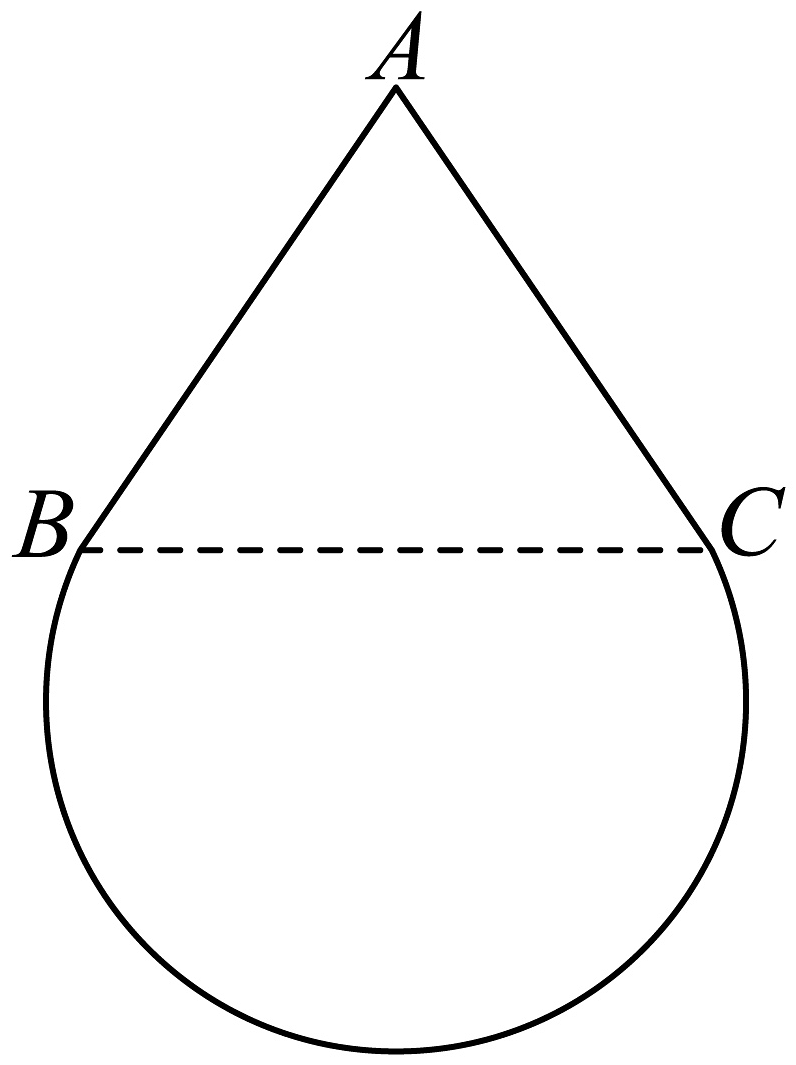 A、 B、 C、 D、
A、 B、 C、 D、 -
6、圆台的上底面半径为1,下底面半径为2,母线长为4.已知P为该圆台某条母线的中点,若一质点从点P出发,绕着该圆台的侧面运动一圈后又回到点P,则该质点运动的最短路径长为( )
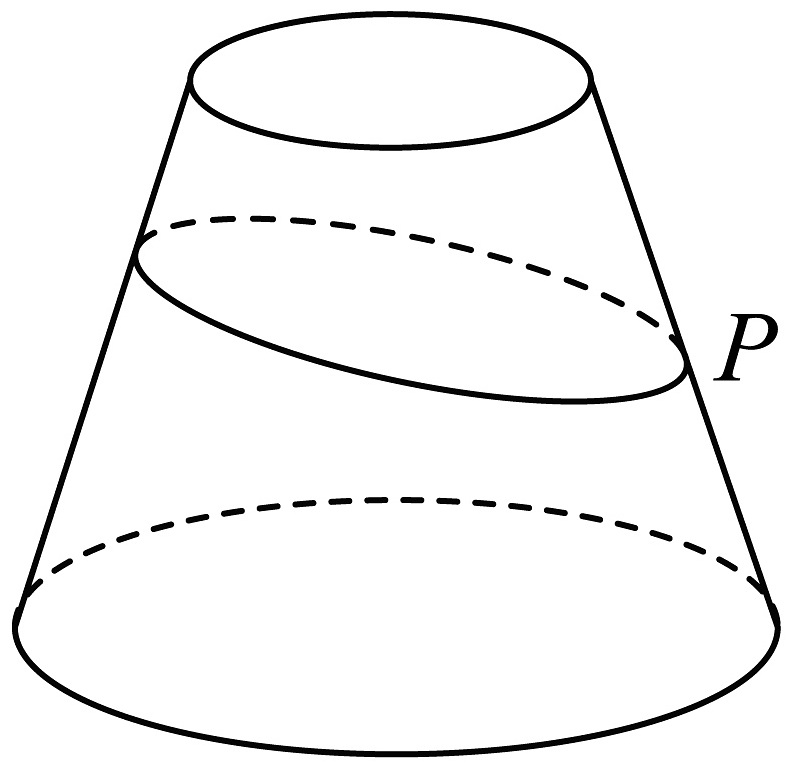 A、 B、6 C、 D、
A、 B、6 C、 D、 -
7、如图,是水平放置的斜二测画法的直观图,的边 , , 则原中角A的角平分线长度是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、已知角 , 满足 , , 则的值为( )A、 B、 C、 D、
-
9、已知复数满足 , 则在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
10、函数的零点所在的区间是( )A、 B、 C、 D、
-
11、若函数的图象上存在个不同点、、、处的切线重合,则称该切线为函数的一条点切线,该函数具有点切线性质.(1)、判断函数 , 的奇偶性并写出它的一条点切线方程(无需理由);(2)、设 , 判断函数是否具有点切线性质,并说明理由;(3)、设 , 证明:对任意的 , , 函数具有点切线性质,并求出所有相应的切线方程.
-
12、椭圆的左右焦点分别为 , 设是第一象限内椭圆上的一点,的延长线交椭圆于点 .
 (1)、若椭圆的离心率 , 求的值;(2)、若 , 求;(3)、若 , 过点的直线与椭圆交于两点,且 , 则当时,判断符合要求的直线有几条,说明理由?
(1)、若椭圆的离心率 , 求的值;(2)、若 , 求;(3)、若 , 过点的直线与椭圆交于两点,且 , 则当时,判断符合要求的直线有几条,说明理由? -
13、如图为正四棱锥为底面的中心.
 (1)、求证:平面 , 平面平面;(2)、设为上的一点, .
(1)、求证:平面 , 平面平面;(2)、设为上的一点, .在下面两问中选一个,
①若 , 求直线与平面所成角的大小.
②已知平面与平面所成锐二面角的大小为 , 若 , 求的长.
-
14、某芯片代工厂生产甲、乙两种型号的芯片,为了解芯片的某项指标,从这两种芯片中各抽取100件进行检测,获得该项指标的频率分布直方图,如图所示:

假设数据在组内均匀分布,以样本估计总体,以事件发生的频率作为相应事件发生的概率.
(1)、求频率分布直方图中x的值并估计乙型芯片该项指标的平均值(同一组中的数据用该组区间的中点值为代表);(2)、已知甲型芯片指标在为航天级芯片,乙型芯片指标在为航天为航天级芯片.现分别采用分层抽样的方式,从甲型芯片指标在内取2件,乙型芯片指标在内取4件,再从这6件中任取2件,求至少有一件为航天级芯片的概率. -
15、已知函数 , 其中(常数且).(1)、若函数的图象过点 , 求关于的不等式的解集;(2)、若存在 , 使得数列是等比数列,求实数的取值范围.
-
16、已知数列不是常数列,前项和为 , . 若对任意正整数 , 存在正整数 , 使得 , 则称是“可控数列”.现给出两个命题:
①若各项均为正整数的等差数列满足公差 , 则是“可控数列”;
②若等比数列是“可控数列”,则其公比 .
则下列判断正确的是( )
A、①与②均为真命题 B、①与②均为假命题 C、①为假命题,②为真命题 D、①为真命题,②为假命题 -
17、在四棱锥中,若 , 则实数组可能是( )A、 B、 C、 D、
-
18、函数 , 则下列命题正确的是( )A、函数是偶函数 B、函数定义域是 C、函数最大值 D、函数的最小正周期为
-
19、在中,“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
20、已知集合是由函数的图象上两两不相同的点构成的点集,集合 , 其中、 . 若集合中的元素按照从小到大的顺序排列能构成公差为的等差数列,当时,则符合条件的点集的个数为 .