-
1、已知和分别是等差数列与等比数列的前项和,且 , , , 则 .
-
2、已知定义域为上的函数满足 , 且 , 记 , 则下列选项中正确的有( )A、 B、当时, C、当时, D、
-
3、已知椭圆:()的左、右焦点分别为 , , 下列命题正确的是( )A、若椭圆上存在一点使 , 则椭圆离心率的取值范围是 B、若椭圆上存在四个点使得 , 则的离心率的取值范围是 C、若椭圆上恰有6个不同的点 , 使得为等腰三角形,则椭圆的离心率的取值范围是 D、若任意以椭圆的上顶点为圆心的圆与椭圆至多3个公共点,则椭圆的离心率的取值范围是
-
4、已知函数 , 则下列选项中正确的是( )A、函数在区间上单调递增 B、函数在的值域为 C、函数在点处的切线方程为 D、关于的方程有2个不同的根当且仅当
-
5、已知 , 方程有实数根,则的最小值为( )A、 B、 C、 D、
-
6、在如图所示的试验装置中,正方形框的边长为2,长方形框的长 , 且它们所在平面形成的二面角的大小为 , 活动弹子分别在对角线和上移动,且始终保持 , 则的长度最小时的取值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、已知双曲线:的左右焦点分别为 , 过点作垂直于轴的直线交双曲线于两点,的内切圆圆心分别为 , 则的周长是( )A、 B、 C、 D、
-
8、已知正项数列的前项积为 , 满足 , 则时的的最小值为( )A、2026 B、2025 C、2024 D、2023
-
9、已知是空间的一个基底,则下列向量中与向量 , 能构成空间基底的是( )A、 B、 C、 D、
-
10、已知函数在处有极大值,则的值为( )A、 B、 C、 D、或
-
11、直线的倾斜角的度数为( )A、 B、 C、 D、
-
12、下列求导正确的( )A、 B、 C、 D、
-
13、牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法—牛顿法.如图,r是函数的零点,牛顿用“作切线”的方法找到了一串逐步逼近r的实数 , , … , , 在点处作的切线,则在处的切线与轴交点的横坐标是 , 同理在处的切线与x轴交点的横坐标是 , 一直继续下去,得到数列 , 从图中可以看到,较接近r,较接近r,……,当n很大时,很小,我们就可以把的值作为r的近似值,即把作为函数的近似零点.现令.
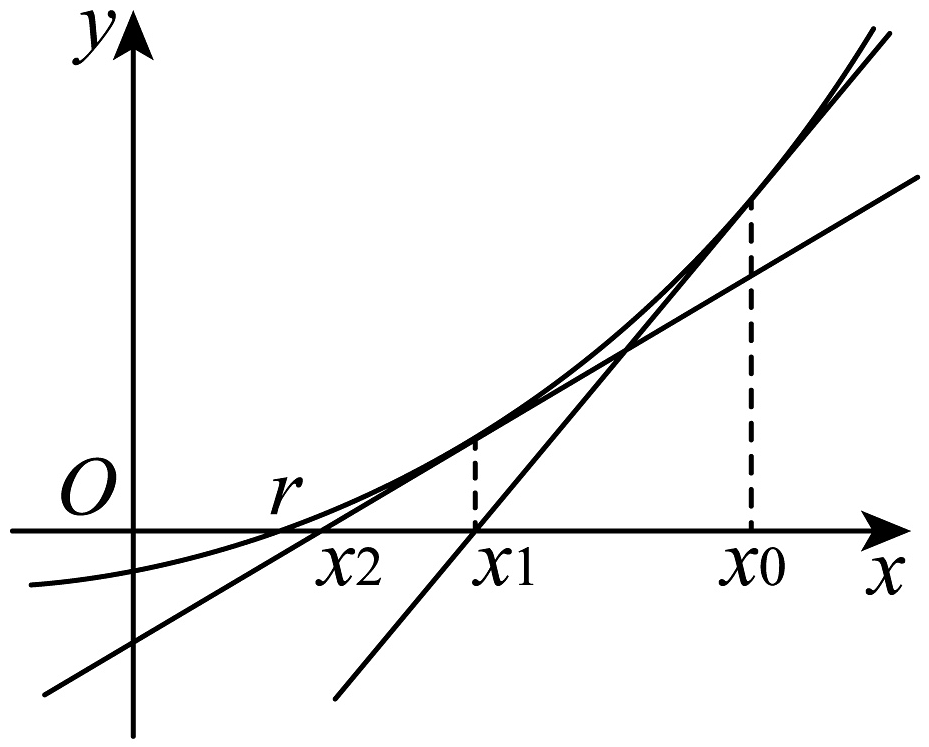 (1)、当时,求的近似解 , ;(2)、在(1)的条件下,求数列的前n项和;(3)、当时,令 , 若时,有两个不同实数根 , .求证:.
(1)、当时,求的近似解 , ;(2)、在(1)的条件下,求数列的前n项和;(3)、当时,令 , 若时,有两个不同实数根 , .求证:. -
14、甲、乙两个不透明的口袋内装有除颜色外大小质地完全相同的若干个小球,已知甲口袋有个红球和4个白球,乙口袋有个红球和2个白球.现在小明从甲口袋有放回地连续摸球2次,每次摸出一个球,然后再从乙口袋有放回地连续摸球2次,每次摸出一个球.(1)、当时.
(i)求小明4次摸球中,至少摸出1个白球的概率;
(ii)设小明4次摸球中,摸出白球的个数为X,求X的分布列和数学期望;
(2)、当时,设小明4次摸球中,恰有3次摸出红球的概率为P,则当m为何值时,P最大? -
15、如图,在等腰梯形中, , , E是的中点, , 将沿着翻折成.
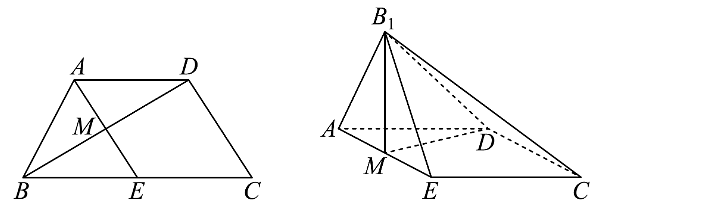 (1)、求证:平面;(2)、若平面平面 , 求平面与平面夹角的余弦值;(3)、在线段上是否存在点P,使得平面 , 若存在,求出的值;若不存在,说明理由.
(1)、求证:平面;(2)、若平面平面 , 求平面与平面夹角的余弦值;(3)、在线段上是否存在点P,使得平面 , 若存在,求出的值;若不存在,说明理由. -
16、在平面直角坐标系中, , , 若点P是平面上一动点,且的周长为 , 设动点P的轨迹为曲线C.(1)、求曲线C的方程;(2)、若直线与曲线C交于A,B两点,且 , , 求k的值.
-
17、记的内角A,B,C所对的边分别为a,b,c,已知.(1)、求角A;(2)、若 , 求外接圆面积的最小值.
-
18、用平面截圆锥可得到不同的圆锥曲线.如图,已知圆锥的侧面积为 , 它的轴截面为等腰直角三角形.过圆锥底面圆心O作平面 , 使圆锥轴与平面成45°角,此时平面截圆锥侧面所得图形记为抛物线C,则抛物线C的焦点到准线的距离为.

-
19、已知曲线 , 圆 , 若直线与曲线在处的切线平行,且直线被圆C截得的弦长为6,则直线的方程为.
-
20、数列是以1为首项,2为公差的等差数列,则.