-
1、函数的单调递减区间是( )A、 B、 C、 D、
-
2、若函数的最大值为 , 则的值为( )A、或 B、或 C、或 D、或
-
3、当时,函数和的图象只可能是( )A、
 B、
B、 C、
C、 D、
D、
-
4、已知全集 , , 则( )A、 B、 C、 D、
-
5、已知为的子集,且 , 则( )A、 B、 C、 D、
-
6、已知 , , 则在上的投影向量为( )A、 B、 C、 D、
-
7、“外观数列”是一类很有趣的数列,该数列由正整数构成,后一项是对它前一项的“外观描述”.例如:取数列第一项为1,将其外观描述为“1个1”,则第二项即为11;将第二项11描述为“2个1”,则第三项即为21;将第三项21描述为“1个2,1个1”,则第四项即为1211;将第四项1211描述为“1个1,1个2,2个1”,则第五项即为111221,将第五项111221描述为“3个1,2个2,1个1”,则第六项即为312211,……,这样每次从左往右将连续相同的数字合并起来描述,给定首项即可依次推出数列后面的每一项.若数列是外观数列,将第n项的各位数字中相同数字连续出现的最大次数记为.例如:外观数列的首项为1时,(1)、若数列是首项为12的外观数列,请直接写出以及.(2)、设集合 , 若外观数列的首项.
(i)探究的最大值,并证明你的结论;
(ii)求所有的 , 使得存在有
-
8、已知函数.(1)、若函数在其定义域上单调递减,求实数a的最小值.(2)、若函数存在两个零点 , 设
(i)求实数m的取值范围;
(ii)证明:.
-
9、已知抛物线()的焦点为 , 过点的动直线与相交于两点,其中点位于第一象限.当时,以为直径的圆与轴相切于点.(1)、求抛物线的方程;(2)、若点在抛物线上,且Γ在点处的切线与直线平行,求面积的最小值以及此时直线的方程.
-
10、已知直三棱柱中, , 分别为和的中点,P为棱上的动点,F为棱上一点,且四点共面.若
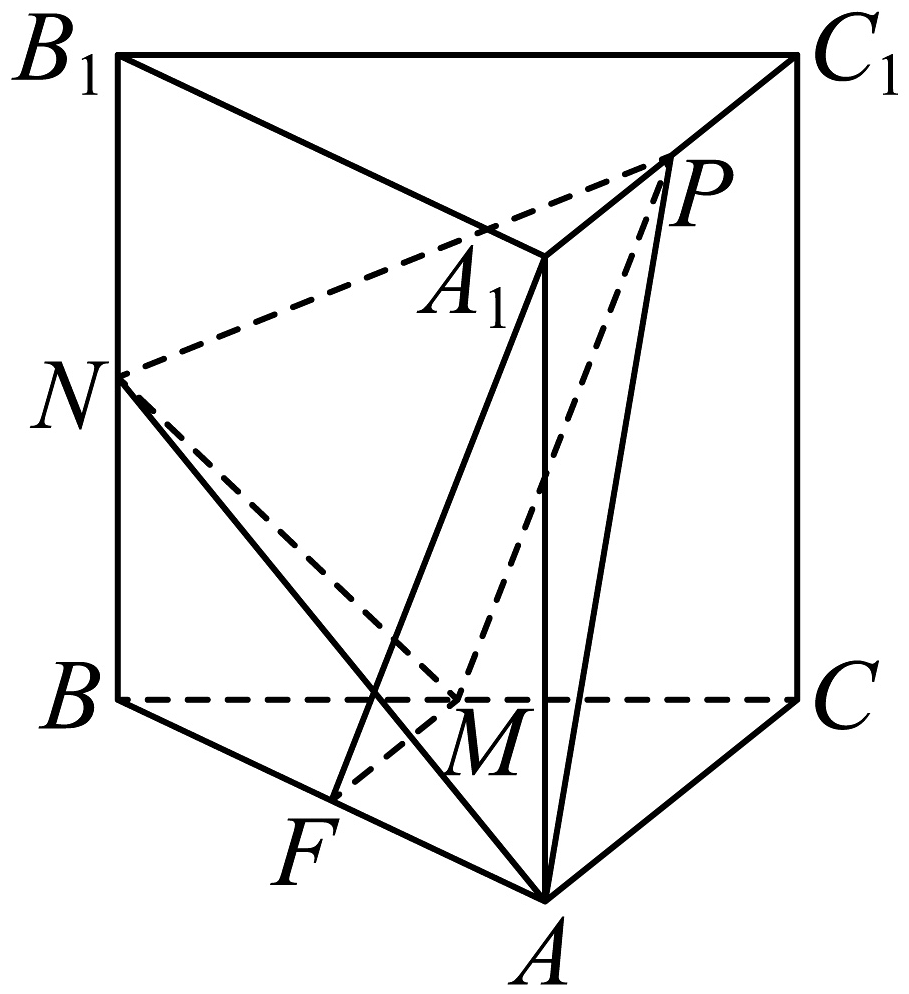 (1)、证明:平面平面;(2)、设是否存在实数λ,使得平面与平面所成的角的余弦值为若存在,求出实数λ,若不存在,请说明理由.
(1)、证明:平面平面;(2)、设是否存在实数λ,使得平面与平面所成的角的余弦值为若存在,求出实数λ,若不存在,请说明理由. -
11、在中,角的对边分别为 , 且(1)、求;(2)、已知为的中点,于于 , 若求的面积.
-
12、绝大多数比赛都采用“局胜制”的规则,但也有一些项目,比如冰壶运动,其整个比赛通常是进行偶数局. 现有甲、乙两名同学进行一项趣味项目的比赛,两人约定比赛规则为:共进行局,谁赢的局数大于局,谁就获得最终胜利. 已知每局比赛中,甲获胜的概率均为乙获胜的概率均为. 记甲赢得整个比赛的概率为. 若则 , 若则当时,最大.
-
13、已知数列{an}满足其前2025项的和为 , 则.
-
14、已知函数 , 为奇函数,其中 , 则
-
15、已知直线(其中与双曲线C:的上支相交于两点,为线段的中点.过点斜率为的两条直线分别与双曲线相交于两点.则下列结论中正确地是( )A、点的坐标满足. B、方程表示的图形是直线和直线 C、直线与直线始终保持平行 D、直线恒过某个定点
-
16、已知函数 , 则下列结论中正确地是( )A、当时, B、的图象关于中心对称 C、若 , 则 D、在上单调递减
-
17、一个袋子中有5个大小相同的球,其中红球3个,白球2个,现从中不放回地随机摸出3个球作为样本,用随机变量X表示样本中红球的个数,用随机变量()表示第次抽到红球的个数,则下列结论中正确地是( )A、X的分布列为 B、X的方差 C、 D、
-
18、三棱锥的所有棱长均为2 , O是的中心,在三棱锥内放置一个以直线为轴的圆柱,则圆柱的体积不能超过( )A、 B、 C、 D、
-
19、已知函数在内单调递增,则在内的零点个数最多为( )A、3 B、4 C、5 D、6
-
20、对任意的 , (且)恒成立,则实数的取值范围是( )A、 B、 C、 D、